
2.4平板应力分析 2.4.1概述(续) 过程设备设计 ◆当变形很大时,面内载荷也会产生弯曲内力,而弯曲 载荷也会产生面内力,所以,大挠度分析要比小挠度 分析复杂的多 ◆本书仅讨论弹性薄板的小挠度理论 7
◆当变形很大时,面内载荷也会产生弯曲内力 ,面内载荷也会产生弯曲内力,而弯曲 载荷也会产生面内力,所以,大挠度分析要比小挠度 ,大挠度分析要比小挠度 分析复杂的多 ◆本书仅讨论弹性薄板的小挠度理论 2.4 平板应力分析 过程设备设计 2.4.1 概述(续) 7

2.4平板应力分析 2.4.1概述(续) 过程设备设计 弹性薄板的小挠度理论建立基本假设-克希霍夫Kirchhoff ① 板弯曲时其中面保持中性,即板中面内各点无伸缩和剪切 变形,只有沿中面法线W的挠度。 只有横向力载荷 ②变形前位于中面法线上的各点,变形后仍位于弹性曲面的同 一法线上,且法线上各点间的距离不变。 类同于梁的平面假设:变形前原为平面的梁的横截面变形后仍 保持为平面,且仍然垂直于变形后的梁轴线。 ③平行于中面的各层材料互不挤压,即板内垂直于板面的正应 力较小,可忽略不计。 8
过程设备设计 弹性薄板的小挠度理论建立基本假设---克希霍夫Kirchhoff ②变形前位于中面法线上的各点,变形后仍位于弹性曲面的同 ,变形后仍位于弹性曲面的同 ① 板弯曲时其中面保持中性,即板中面内各点无伸缩和剪切 变形,只有沿中面法线 ,只有沿中面法线 ωw的挠度 。 只有横向力载荷 2.4 平板应力分析 2.4.1 概述(续) 8 一法线上,且法线上各点间的距离不变 ,且法线上各点间的距离不变 。 类同于梁的平面假设:变形前原为平面的梁的横截面变形后仍 :变形前原为平面的梁的横截面变形后仍 保持为平面,且仍然垂直于变形后的梁轴线 ,且仍然垂直于变形后的梁轴线 。 ③平行于中面的各层材料互不挤压,即板内垂直于板面的正应 ,即板内垂直于板面的正应 力较小,可忽略不计
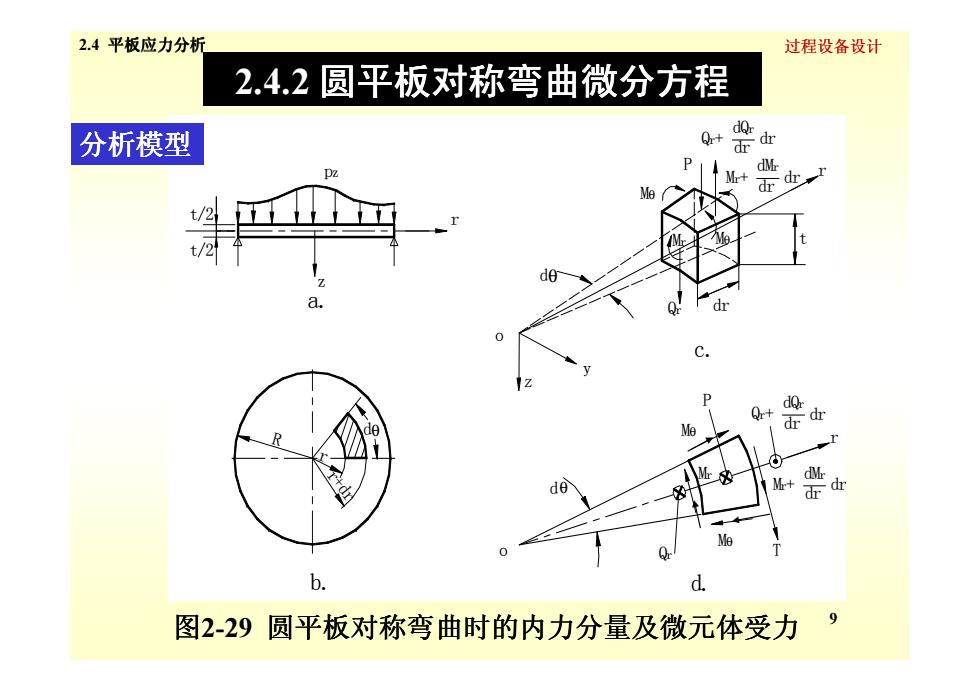
2.4平板应力分析 过程设备设计 2.4.2圆平板对称弯曲微分方程 分析模型 Qr+ d d证d dMr pz + dr drr t/2 t/2 de Qr+ d drdr dMr Mr+ dd Me b. d 图2-29圆平板对称弯曲时的内力分量及微元体受力 9
过程设备设计 2.4.2 圆平板对称弯曲微分方程 t/2 t/2 z dθ Qr dr t r Qr+ P Mθ Mr Mθ o a. c. pz r dQr dr dr dr Mr+ dMr dr 分析模型 2.4 平板应力分析 图 9 2-29 圆平板对称弯曲时的内力分量及微元体受力 r+dr dθ z dθ P T Mθ Mθ o Qr r b. c. d. Mr dMr Mr+ dr dr dr Qr+ dQr dr y R r

2.4平板应力分析 过程设备设计 2.4.2圆平板对称弯曲微分方程(续) 分析模型 半径R,厚度t的圆平板 受轴对称载荷P, 在”、0、z圆柱坐标系中 内力:M,、M、Q三个内力分量 轴对称性 几何对称,载荷对称,约束对称, 在r、0、z圆柱坐标系中 挠度W只是r的函数,而与0无关。 10
过程设备设计 分析模型 半径R,厚度t的圆平板 受轴对称载荷Pz 内力:Mr、Mθ、Qr 三个内力分量 在r、θ、z圆柱坐标系中 2.4.2 圆平板对称弯曲微分方程 圆平板对称弯曲微分方程(续) 2.4 平板应力分析 10 轴对称性 几何对称,载荷对称,约束对称, 在r、θ、z圆柱坐标系中 挠度 w 只是 r 的函数,而与θ无关

2.4平板应力分析 过程设备设计 2.4.2圆平板对称弯曲微分方程(续) 挠度微分方程的建立: 基于平衡、几何、物理方程 微元体: 用半径为r和r+dr的 两个圆柱面和夹角为 d0的两个径向截面截 出板上一微元体如图2 -29(a)、(b) (b) 图2-29圆平板对称弯曲时的 内力分量及微元体受力
过程设备设计 挠度微分方程的建立: 微元体: 用半径为r和r+dr的 两个圆柱面和夹角为 dθ R r 基于平衡、几何、物理方程 2.4 平板应力分析 2.4.2 圆平板对称弯曲微分方程 圆平板对称弯曲微分方程(续) 11 两个圆柱面和夹角为 dθ的两个径向截面截 出板上一微元体如图2 -29(a)、(b) r+dr r (b) 图2-29 圆平板对称弯曲时的 内力分量及微元体受力