
高(中)考试题主要从以下几个方 面对数学思想方法进行考查: 法用整法搀臂定系频 ② 数学逻辑方法:,分析法、综合法、反证法、 归纳法、演绎法等; ③ 数学思维方法:观察与分析、概括与抽象、 分析与综合、特殊写一般、类比、归纳和演绎 ④ 常用数学思想:函数与方程思想、数形结合 思想、分类讨论思想、转化(化归)思想等
高(中 )考试题主要从以下几个方 面对数学思想方法进行考查: ① 常用数学方法:配方法、换元法、待定系数 法、数学归纳法、参数法、消元法等; ② 数学逻辑方法:分析法、综合法、反证法、 归纳法、演绎法等; ③ 数学思维方法:观察与分析、概括与抽象、 分析与综合、特殊与一般、类比、归纳和演绎 等; ④ 常用数学思想:函数与方程思想、数形结合 思想、分类讨论思想、转化(化归)思想等

三、数学思想方法指导解题 配方法、换元法、待 数学一般方法 定条数法、判别式法 、割补法等 敷学思想 逻辑学中的方法 分析法、综合法、归 和方法 (或思维方法) 纳法、反证法等 函数和方程思想、分 数学思想方法 类讨论思想、数形结 合思想、化归思想等
三、数学思想方法指导解题 数学思想 和方法 数学一般方法 逻辑学中的方法 (或思维方法) 数学思想方法 配方法、换元法、待 定系数法、判别式法 、割补法等 分析法、综合法、归 纳法、反证法等 函数和方程思想、分 类讨论思想、数形结 合思想、化归思想等

函数思想 ·分析或研究具体问题中的数量关系,把 这种数量关系转化为函数的形式,利用 函数的相关知识和方法解决问题的思维 方式称函数思想。 ●】 本质特征:用变量和函数思考,体现了 运动、变化、联系的辩证唯物主义观点
函数思想 • 分析或研究具体问题中的数量关系,把 这种数量关系转化为函数的形式,利用 函数的相关知识和方法解决问题的思维 方式称函数思想 。 • 本质特征:用变量和函数思考,体现了 运动、变化、联系的辩证唯物主义观点
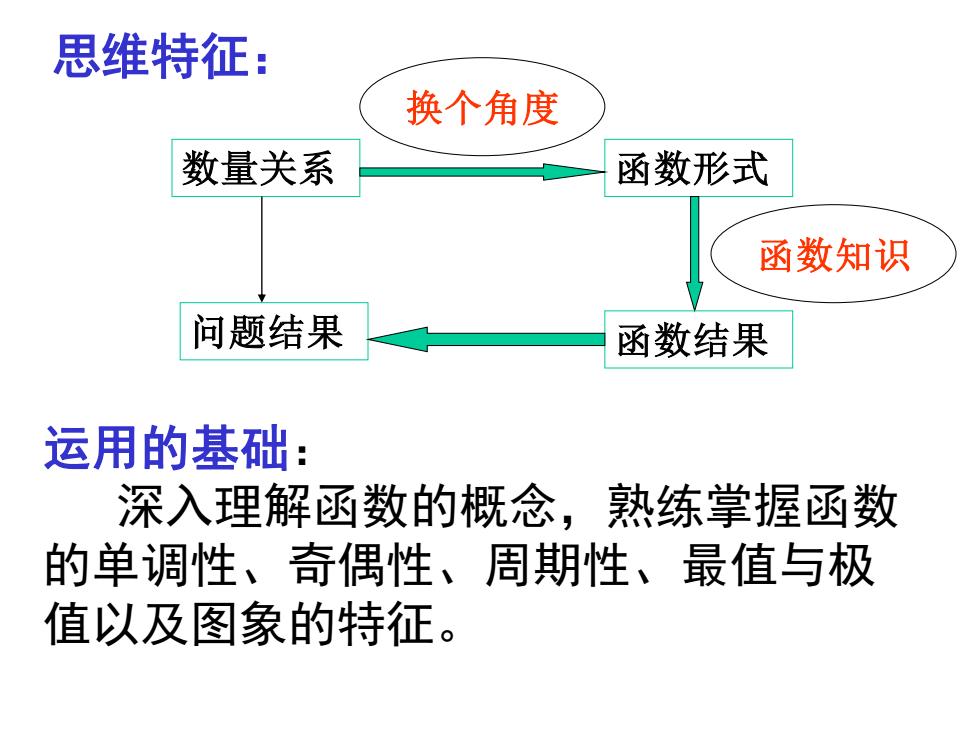
思维特征: 换个角度 数量关系 函数形式 函数知识 问题结果 函数结果 运用的基础: 深入理解函数的概念,熟练掌握函数 的单调性、奇偶性、周期性、最值与极 值以及图象的特征
数量关系 函数形式 问题结果 函数结果 函数知识 换个角度 思维特征: 运用的基础: 深入理解函数的概念,熟练掌握函数 的单调性、奇偶性、周期性、最值与极 值以及图象的特征

运用的基础: 深入理解函数的概念,熟练掌握函 数的单调性、奇偶性、周期性、最值与 极值以及图象的特征。 运用的关键 : 挖掘问题的隐含条件,构造出恰 当的函数模型,并灵活地运用函数的 图象与性质
运用的关键: 挖掘问题的隐含条件,构造出恰 当的函数模型,并灵活地运用函数的 图象与性质。 运用的基础: 深入理解函数的概念,熟练掌握函 数的单调性、奇偶性、周期性、最值与 极值以及图象的特征