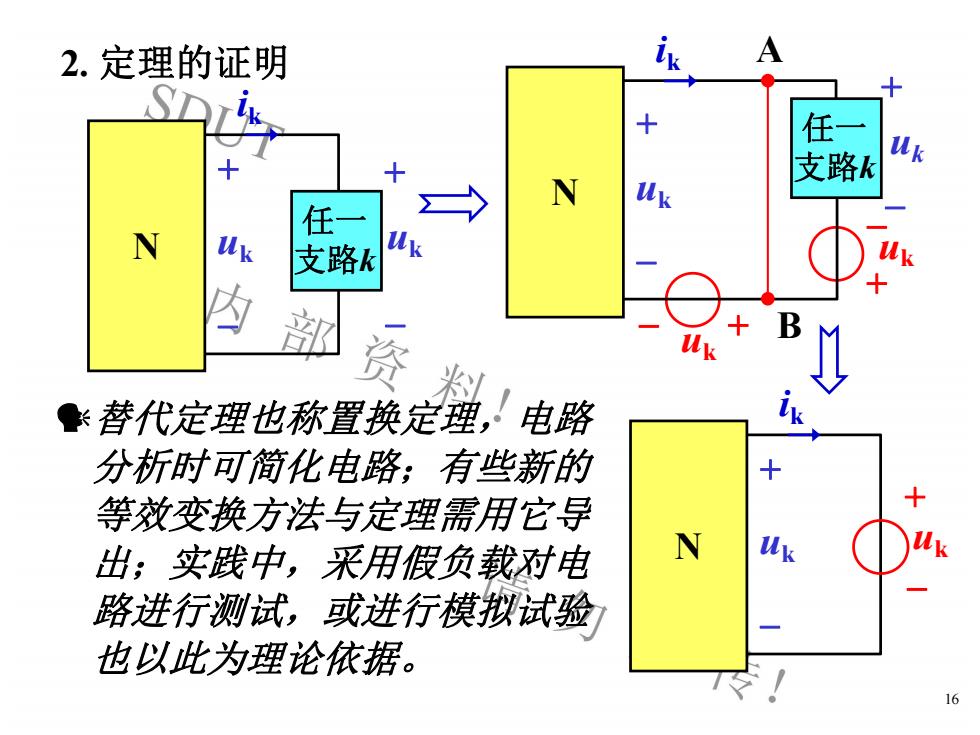
Aik2.定理的证明十SALik+任一Uk支路k十+NukV任ukNuku支路k为B部资料Muk替代定理也称置换定理,!电路A长分析时可简化电路:有些新的+等效变换方法与定理需用它导ukNuk出:实践中,采用假负载对电路进行测试,或进行模拟试验也以此为理论依据。16
16 2. 定理的证明 ik N + -uk 任一 支路k + -uk - + uk - + uk ik N + -uk + -uk 任一 支路k ik N + -uk + -uk 替代定理也称置换定理,电路 分析时可简化电路;有些新的 等效变换方法与定理需用它导 出;实践中,采用假负载对电 路进行测试,或进行模拟试验 也以此为理论依据。 A B
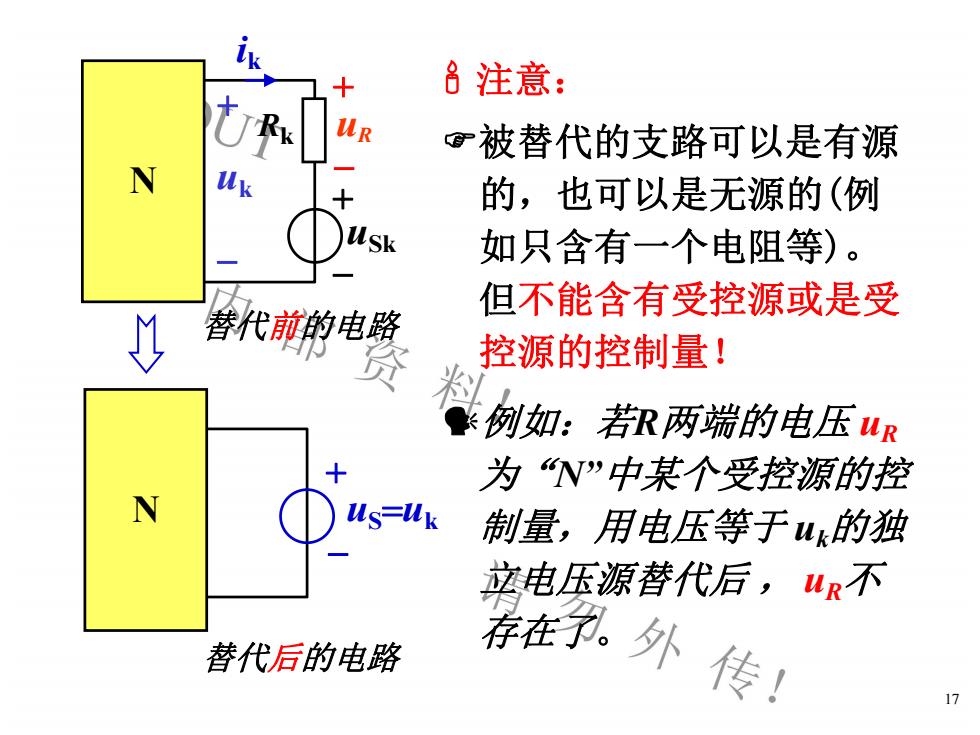
吕注意:+URkUR百被替代的支路可以是有源Nuk的,也可以是无源的(例+usk如只含有一个阻等)。但不能含有受控源或是受替代前的电路控源的控制量!资料例如:若R两端的电压UR为“N"中某个受控源的控十Nus-uk制量,用电压等于u的独立电压源替代后,ur不存在予。外传!替代后的电路17
17 注意: 被替代的支路可以是有源 的,也可以是无源的(例 如只含有一个电阻等)。 但不能含有受控源或是受 控源的控制量! + -uR uSk ik + - Rk + -uk 替代前的电路 N uS=uk + - 替代后的电路 N 例如:若R两端的电压 uR 为“N”中某个受控源的控 制量,用电压等于 uk的独 立电压源替代后 , uR不 存在了

3.说明(1)替代定理既适用于线性电路,也适用于非线性电路。?2.5A(2)替代后电路必须有唯一解。++++?即替代后不能形成纯5V10V51电压源回路和纯电流源结点(含广义结点)。料(3)替代后其余支路及参数不能改变。(4)被替代的支路可以是有源的,也可以是无源的(例如只含有一个电阻等)。但不能含有受控源或A勿外传!是受控源的控制量!18
18 3.说明 即替代后不能形成纯 电压源回路和纯电流 源结点(含广义结点)。 1.5A 2.5A 1A 10V 5V 2 5 + - - + 2.5A 10V 5V + - - + 5V +- ? 2.5A ? (4)被替代的支路可以是有源的,也可以是无源的 (例如只含有一个电阻等)。但不能含有受控源或 是受控源的控制量! (3)替代后其余支路及参数不能改变。 (1)替代定理既适用于线性电路,也适用于非线性电路。 (2)替代后电路必须有唯一解
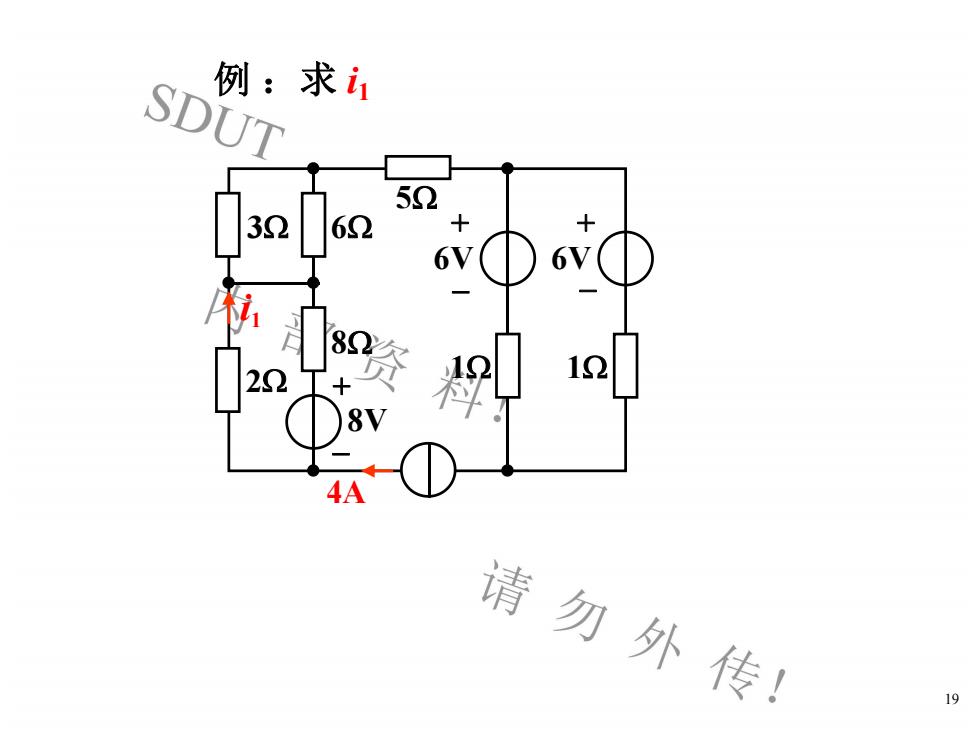
例:求iSDUT523262611821222+8V4A请勿外传!19
19 例 :求 i1 + - i1 8V 3 6 5 8 2 4A + - 6V 1 + - 6V 1
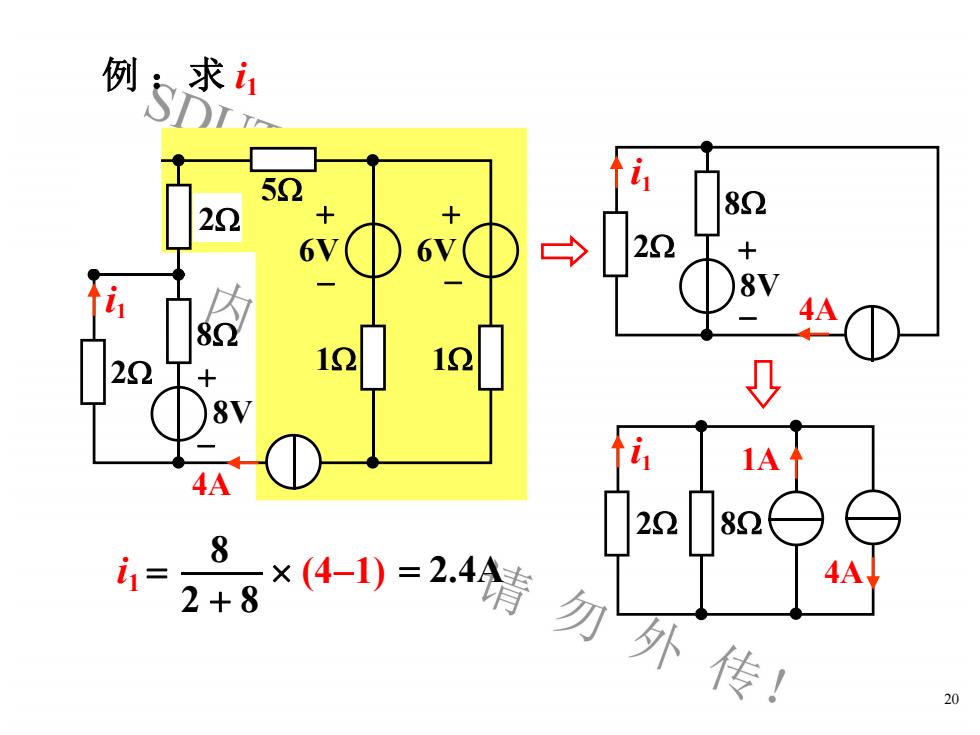
例:求iSDL1528222226+6-8V82121222+8Vi1A4A22828)=2.4情勿外传!(4-1)4AIX2 +820
20 例 :求 i1 +- i1 8V 3 6 5 8 2 4A +-6V1 +- 6V1 2 +- i1 8V 8 2 4A i12 8 4A 1A i1 = 2 + 8 8 (4-1) = 2.4A