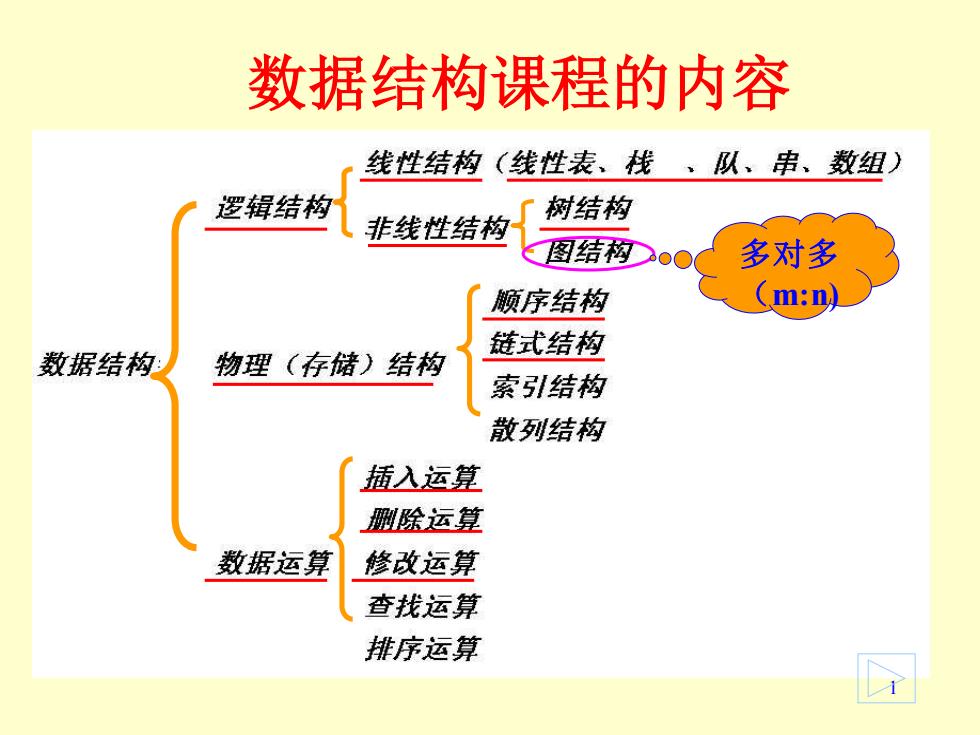
数据结构课程的内容 线性结构(线性表、栈、队、串、数组) 逻辑结构 非线性结构 树结构 图结构00 多对多 颜序结构 (m:ω 链式结构 数据结构 物理(存储)结构 索引结构 散列结构 插入运算 删除运草 数据运算 修改运算 查找运算 排序运算
1 数据结构课程的内容 多对多 (m:n)

第7章1 图 7.1基本术语 7.2存储结构 7.3图的遍历 7.4图的连通性 7.5图的应用 2
2 7.1 基本术语 7.2 存储结构 7.3 图的遍历 7.4 图的连通性 7.5 图的应用 第7章 图
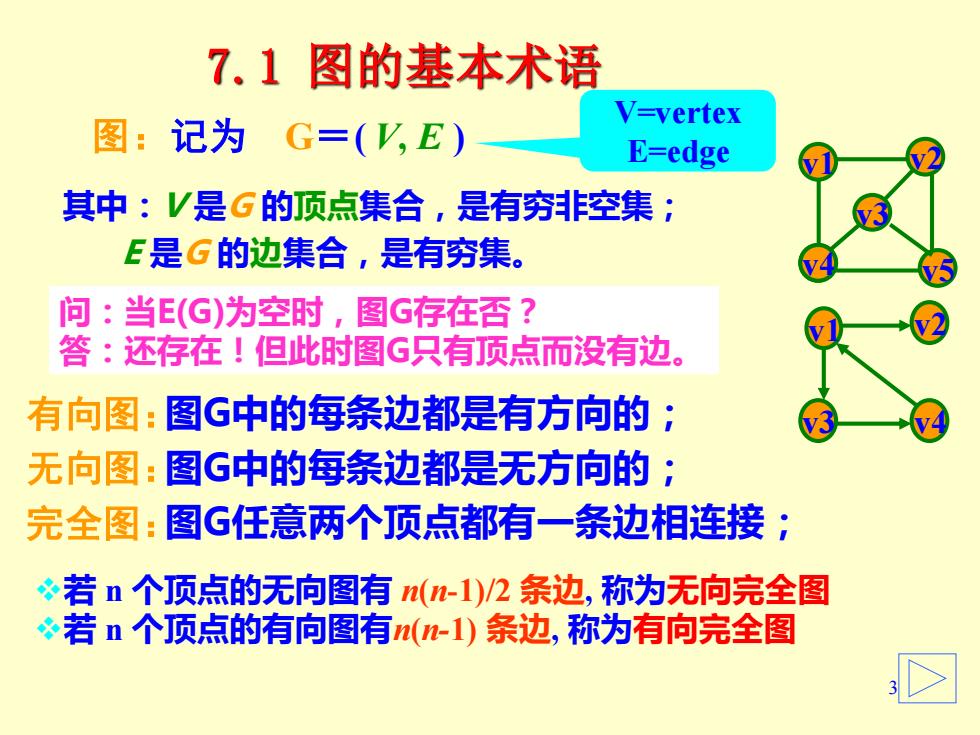
7.1图的基本术语 V=vertex 图:记为G=(V,E) E=edge 其中:V是G的顶点集合,是有穷非空集; E是G的边集合,是有穷集。 问:当E(G)为空时,图G存在否? 答:还存在!但此时图G只有顶点而没有边。 有向图:图G中的每条边都是有方向的; 无向图:图G中的每条边都是无方向的; 完全图:图G任意两个顶点都有一条边相连接; 若n个顶点的无向图有(n-1)/2条边,称为无向完全图 ÷若n个顶点的有向图有(-1)条边,称为有向完全图
3 7.1 图的基本术语 其中:V 是G 的顶点集合,是有穷非空集; E 是G 的边集合,是有穷集。 问:当E(G)为空时,图G存在否? 答:还存在!但此时图G只有顶点而没有边。 有向图: 无向图: 完全图: 图G中的每条边都是有方向的; 图G中的每条边都是无方向的; 图G任意两个顶点都有一条边相连接; ❖若 n 个顶点的无向图有 n(n-1)/2 条边, 称为无向完全图 ❖若 n 个顶点的有向图有n(n-1) 条边, 称为有向完全图 V=vertex 图:记为 G= E=edge ( V, E ) v1 v2 v3 v4 v5 v1 v2 v3 v4
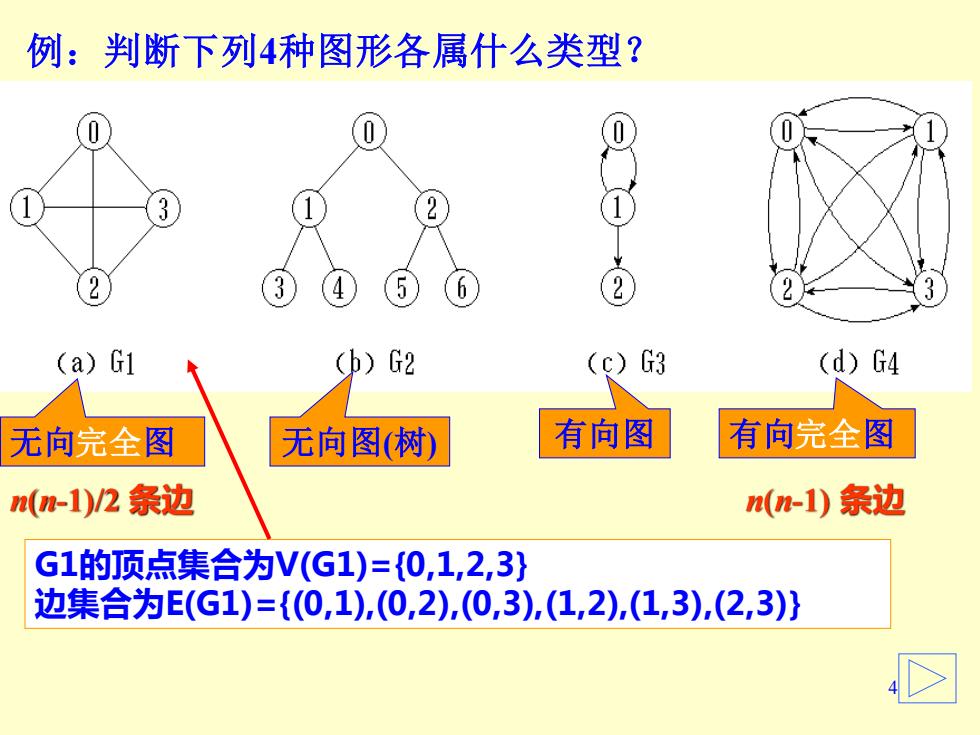
例:判断下列4种图形各属什么类型? 1 2 (a)G1 G2 (c)3 (d)G4 无向完全图 无向图(树) 有向图 有向完全图 (n-1)/2条边 n(n-1)条边 G1的顶点集合为V(G1)={0,1,2,3} 边集合为E(G1)={(0,1),(0,2),(0,3)(1,2),(1,3),(2,3)}
4 例:判断下列4种图形各属什么类型? 无向 无向图(树) 有向图 有向 n(n-1)/2 条边 n(n-1) 条边 G1的顶点集合为V(G1)={0,1,2,3} 边集合为E(G1)={(0,1),(0,2),(0,3),(1,2),(1,3),(2,3)} 完全图 完全图
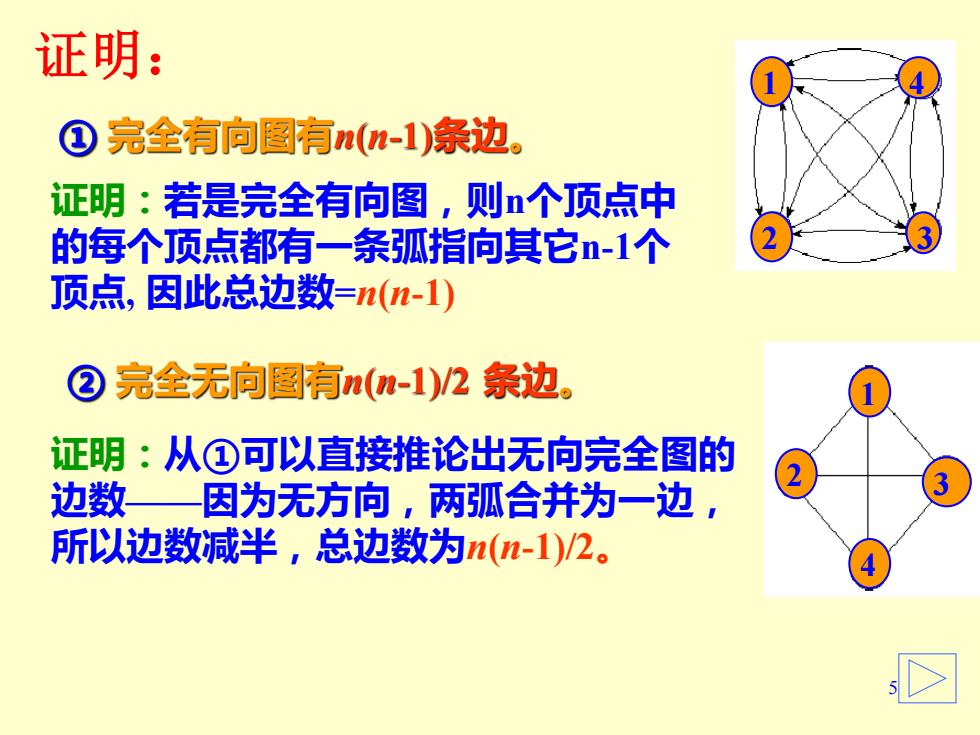
证明: ①完全有向图有n(n-1)条边。 证明:若是完全有向图,则n个顶点中 的每个顶点都有一条弧指向其它n-1个 顶点,因此总边数=n(n-1) ② 完全无向图有n(n-1)/2条边。 证明:从①可以直接推论出无向完全图的 边数— 因为无方向,两弧合并为一边, 3 所以边数减半,总边数为n(n-1)/2
5 证明: 证明:若是完全有向图,则n个顶点中 的每个顶点都有一条弧指向其它n-1个 顶点, 因此总边数=n(n-1) 证明:从①可以直接推论出无向完全图的 边数——因为无方向,两弧合并为一边, 所以边数减半,总边数为n(n-1)/2。 ② 完全无向图有n(n-1)/2 条边。 ① 完全有向图有n(n-1)条边。 1 2 3 4 1 2 3 4