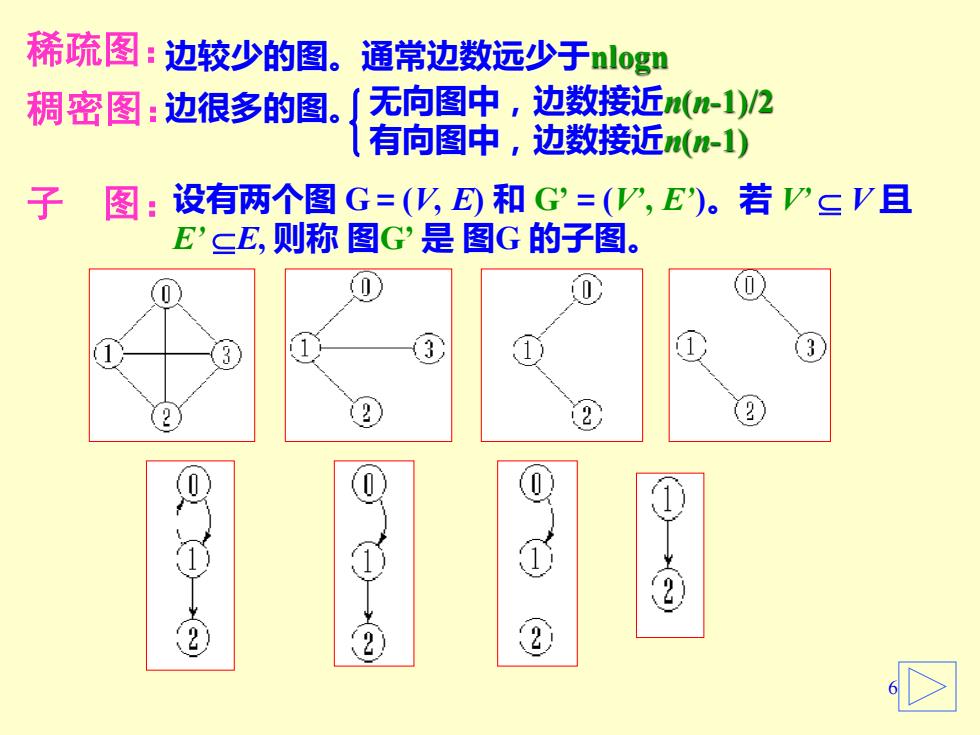
稀疏图:边较少的图。通常边数远少于logn 稠密图:边很多的图。 无向图中,边数接近n(n-1)/2 1有向图中,边数接近n(-1) 子 图:设有两个图G=(W,E)和G=(W,E)。若P∈V且 E'三E,则称图G'是图G的子图。 (0 (0 1 ① ① 3 2 0) ②
6 稀疏图: 稠密图: 设有两个图 G=(V, E) 和 G’=(V’, E’)。若 V’ V 且 E’ E, 则称 图G’ 是 图G 的子图。 子 图: 边较少的图。通常边数远少于nlogn 边很多的图。 无向图中,边数接近n(n-1)/2 有向图中,边数接近n(n-1)

带权图:即边上带权的图。其中权是指每条边 可以标上具有某种含义的数值(即与 边相关的数)。 网络:→带权图 连通图:在无向图中,若从顶点到顶点2有 路径,则称顶点M与是连通的。如 果图中任意一对顶点都是连通的,则 称此图是连通图。 非连通图的极大连通子图叫做连通 分量。 强连通图:在有向图中,若对于每一对顶点和y, 都存在一条从到y和从y到的路径, 则称此图是强连通图。 非强连通图的极大强连通子图叫做强连通分量
7 带权图:即边上带权的图。其中权是指每条边 可以标上具有某种含义的数值(即与 边相关的数)。 连通图:在无向图中, 若从顶点v1到顶点v2有 路径, 则称顶点v1与v2是连通的。如 果图中任意一对顶点都是连通的, 则 称此图是连通图。 非连通图的极大连通子图叫做连通 分量。 →带权图 在有向图中, 若对于每一对顶点vi和vj , 都存在一条从vi到vj和从vj到vi的路径, 则称此图是强连通图。 强连通图: 网 络: D E A B C F J L M G H I K 非强连通图的极大强连通子图叫做强连通分量
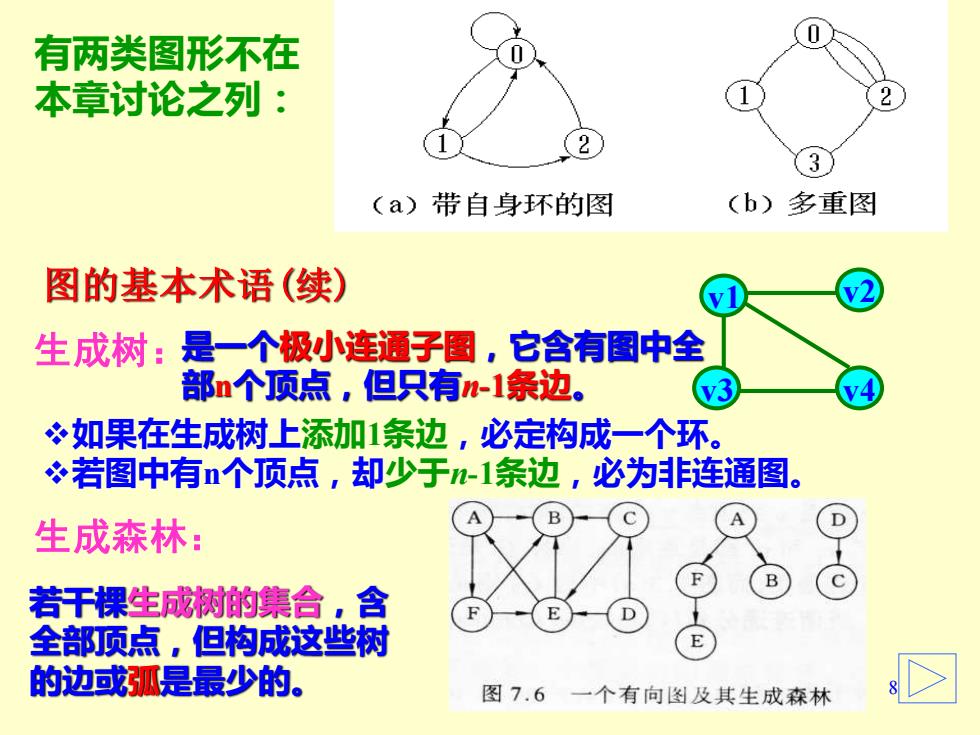
有两类图形不在 本章讨论之列: 3 (a)带自身环的图 (b)多重图 图的基本术语(续) 生成树:是一个极小连通子圆,它含有图中全 部n个顶点,但只有-1条边。 3 冬如果在生成树上添加1条边,必定构成一个环。 若图中有n个顶点,却少于-1条边,必为非连通图。 B 生成森林: 若干棵生成树的集合,含 全部顶点,但构成这些树 的边或弧是最少的。 图7.6一个有向图及其生成森林
8 生成树:是一个极小连通子图,它含有图中全 部n个顶点,但只有n-1条边。 若干棵生成树的集合,含 全部顶点,但构成这些树 的边或弧是最少的。 有两类图形不在 本章讨论之列: 图的基本术语(续) v1 v2 v3 v4 ❖如果在生成树上添加1条边,必定构成一个环。 ❖若图中有n个顶点,却少于n-1条边,必为非连通图。 生成森林:
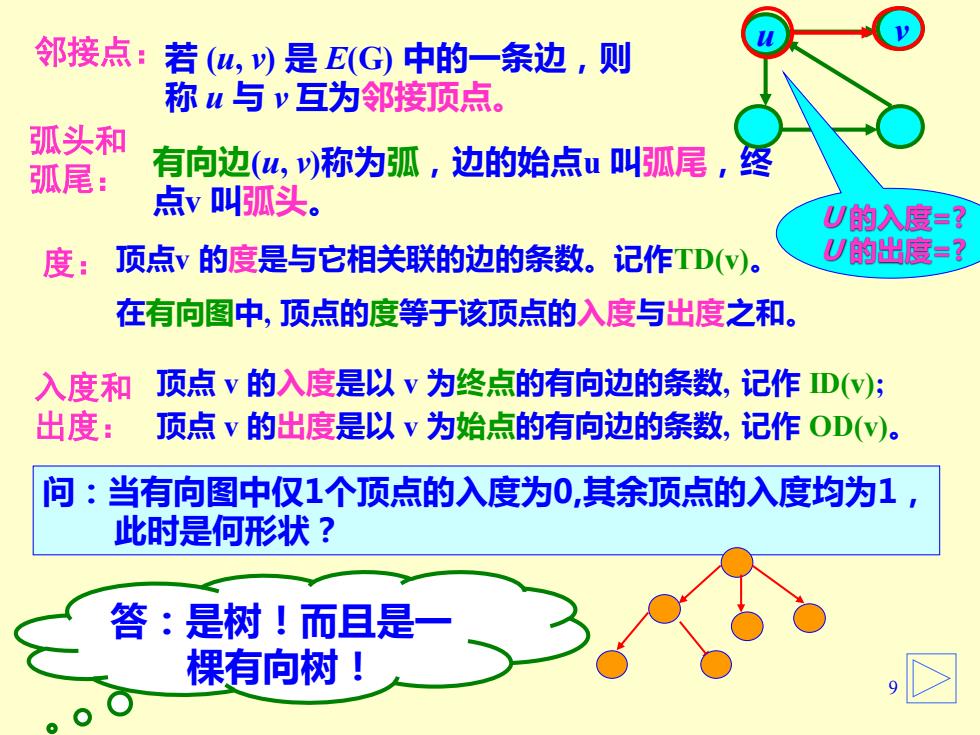
邻接点:若(u,)是E(G)中的一条边,则 称u与v互为邻接顶点。 弧头和 弧尾: 有向边(山,)称为弧,边的始点u叫弧尾,经 点v叫弧头。 U的入度=? 度:顶点v的度是与它相关联的边的条数。记作TD(w)。 U的出度=? 在有向图中,顶点的度等于该顶点的入度与出度之和。 入度和顶点v的入度是以v为终点的有向边的条数,记作D(v; 出度: 顶点v的出度是以v为始点的有向边的条数,记作OD(W)。 问:当有向图中仅1个顶点的入度为0,其余顶点的入度均为1, 此时是何形状? 答:是树!而目是一 棵有向树」
9 邻接点: 有向边(u, v)称为弧,边的始点u 叫弧尾,终 点v 叫弧头。 顶点 v 的入度是以 v 为终点的有向边的条数, 记作 ID(v); 顶点 v 的出度是以 v 为始点的有向边的条数, 记作 OD(v)。 若 (u, v) 是 E(G) 中的一条边,则 称 u 与 v 互为邻接顶点。 弧头和 弧尾: 入度和 出度: 问:当有向图中仅1个顶点的入度为0,其余顶点的入度均为1, 此时是何形状? u v 度: 顶点v 的度是与它相关联的边的条数。记作TD(v)。 在有向图中, 顶点的度等于该顶点的入度与出度之和。 U 的入度=? U 的出度=? 答:是树!而且是一 棵有向树!
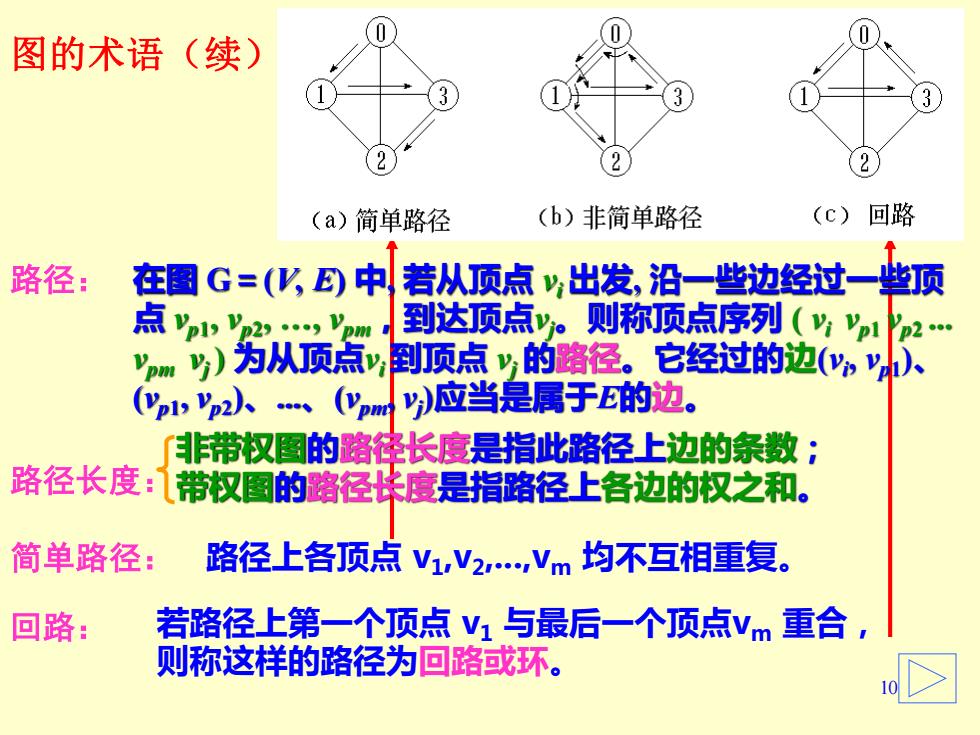
(0 图的术语(续) 3 3 2 (a)简单路径 (b)非简单路径 (c)回路 路径: 在图G=(KE中! 若从顶点y,出发,沿一些边经过一坐顶 点p"2 Vpm 到达顶点y。则称顶点序列(片2 Vpm )为从顶点到顶点的略径。它经过的边(以、 (pp2以、(ypm)应当是属于E的边。 非带权图的路锋长度是指此路径上边的条数: 路径长度: 带权图的路径珠度是指路径上各边的权之和。 简单路径: 路径上各顶点V1,V2,Vm均不互相重复。 回路: 若路径上第一个顶点V1与最后一个顶点vm重合, 则称这样的路径为回路或环
10 简单路径: 路径上各顶点 v1 ,v2 ,.,vm 均不互相重复。 回路: 若路径上第一个顶点 v1 与最后一个顶点vm 重合, 则称这样的路径为回路或环。 路径: 在图 G=(V, E) 中, 若从顶点 vi 出发, 沿一些边经过一些顶 点 vp1 , vp2 , ., vpm,到达顶点vj。则称顶点序列 ( vi vp1 vp2 . vpm vj ) 为从顶点vi 到顶点 vj 的路径。它经过的边(vi , vp1 )、 (vp1 , vp2 )、.、(vpm, vj )应当是属于E的边。 路径长度: 非带权图的路径长度是指此路径上边的条数; 带权图的路径长度是指路径上各边的权之和。 图的术语(续)