
第5章 数组和广义表(Arrays&Lists) 数组和广义表的特点: 表中元素也是一个线性表,即广义的线性表 5.1数组的定义 5.2数组的顺序表示和实现 5.3 矩阵的压缩存储 5.4广义表的定义 5.5 广义表的存储结构 1
1 第5章 数组和广义表(Arrays & Lists) 5.1 数组的定义 5.2 数组的顺序表示和实现 5.3 矩阵的压缩存储 5.4 广义表的定义 5.5 广义表的存储结构 数组和广义表的特点: 表中元素也是一个线性表,即广义的线性表

5.3矩阵的压缩存储 重点介绍稀疏矩阵的压缩和相应的操作。 做加减操作时 很方便 一、稀疏矩阵的压缩存储 有4种压缩方式:线性表、 十字链表、三元组表、 带辅助向量的三元组表 做转置操作时 很方便 二、稀疏矩阵的操作 2
2 5.3 矩阵的压缩存储 重点介绍稀疏矩阵的压缩和相应的操作。 一、稀疏矩阵的压缩存储 二、稀疏矩阵的操作 有4种压缩方式:线性表、十字链表、三元组表、 带辅助向量的三元组表 做加减操作时 很方便 做转置操作时 很方便
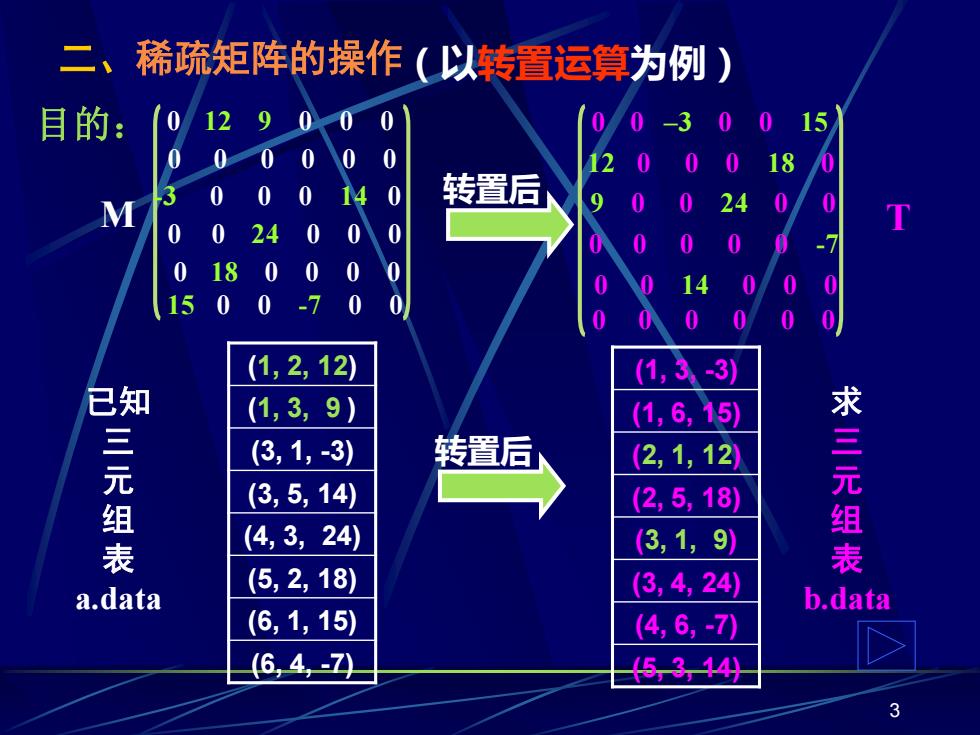
二、稀疏矩阵的操作(以转置运算为例) 目的: 1012900 0 15 0 000 0 0 00014 M 0 转置后 00240 0 0 018000 0 1500-7 0 0 (1,2,12) (1,3 -3} 已知 (1,3,9) (1,6,15】 求 三元组 (3,1,3) 转置后 (2,1,12) (3,5,14) (2,5,18) 三元组 (4,3,24) 3,1,9】 (5,2,18) a.data (3,4,24) b.data (6,1,15) (4,6,-7 (6,4,-Z 344
3 二、稀疏矩阵的操作 0 12 9 0 0 0 0 0 0 0 0 0 -3 0 0 0 14 0 0 0 24 0 0 0 0 18 0 0 0 0 15 0 0 -7 0 0 0 0 –3 0 0 15 12 0 0 0 18 0 9 0 0 24 0 0 0 0 0 0 0 -7 0 0 14 0 0 0 0 0 0 0 0 0 (1, 2, 12) (1, 3, 9 ) (3, 1, -3) (3, 5, 14) (4, 3, 24) (5, 2, 18) (6, 1, 15) (6, 4, -7) (1, 3, -3) (1, 6, 15) (2, 1, 12) (2, 5, 18) (3, 1, 9) (3, 4, 24) (4, 6, -7) (5, 3, 14) 已知 三 元 组 表 a.data 求 三 元 组 表 b.data 转置后 M T (以转置运算为例) 目的: 转置后

有两种实现 压缩转置 转置的方法 快速(压缩)转置 压缩转置的思路:反复扫描a表(记为a.data)y中的 列序,从=1~n依次进行转置。 快速转置的思路:依次把a.data中的元素直接送入b.data 的恰当位置上(即a.data三元组的p指针不回溯)。 关键:怎样寻找b.data的"恰当”位置?
4 有两种实现 转置的方法 压缩转置 快速(压缩)转置 压缩转置的思路:反复扫描a表(记为a.data)中的 列序,从j=1~n依次进行转置。 快速转置的思路:依次把a.data中的元素直接送入b.data 的恰当位置上(即a.data三元组的p指针不回溯)。 关键:怎样寻找b.data的“恰当”位置?
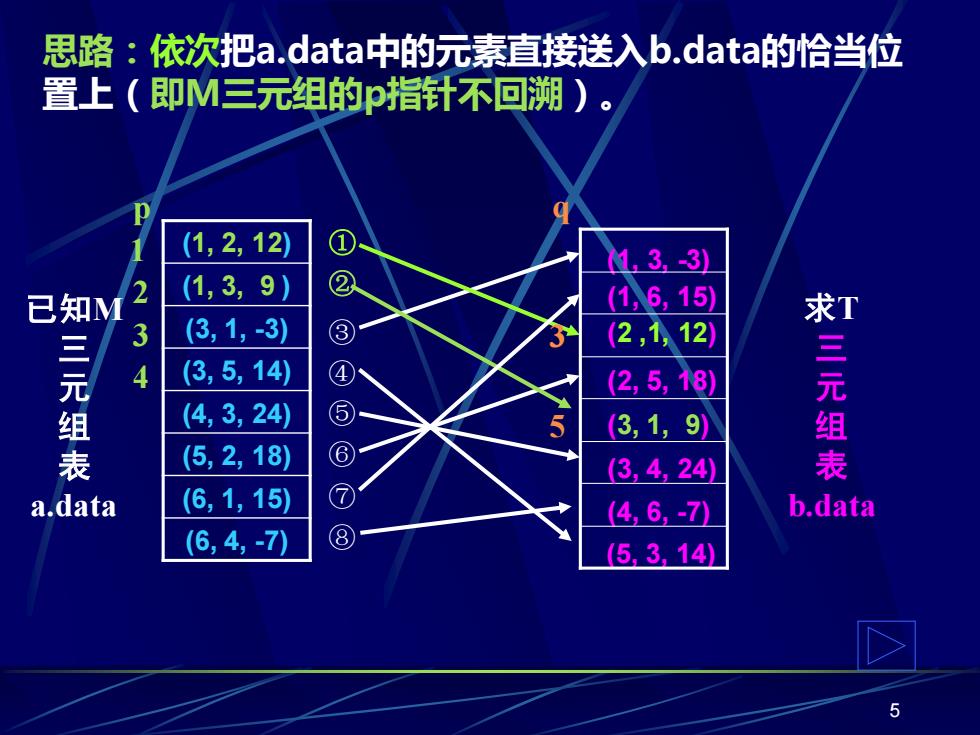
思路:依次把a.data中的元素直接送入b.data的恰当位 置上(即M三元组的指针不回溯)。 (1,2,12) M,3.3 已知M 2 (1,3,9) ② (16,15) (3,1,3) ③ 2,1,12 是 4 (3,5,14) ④ (2,5,18) 组表 (4,3,24) ⑤ 3,1,9) 求三元组表 (5,2,18) ⑥ (3,4,24 a.data (6,1,15) ⑦ 46,-70 data (6,4,-7) ⑧ 5,3,14
5 已知M 三 元 组 表 a.data 求T 三 元 组 表 b.data ③ (1, 3, -3) ① (2 ,1, 12) ⑥ (2, 5, 18) ② (3, 1, 9) ⑧ (4, 6, -7) ④ (5, 3, 14) ⑦ (1, 6, 15) ⑤ (3, 4, 24) (1, 2, 12) (1, 3, 9 ) (3, 1, -3) (3, 5, 14) (4, 3, 24) (5, 2, 18) (6, 1, 15) (6, 4, -7) 思路:依次把a.data中的元素直接送入b.data的恰当位 置上(即M三元组的p指针不回溯)。 p 1 2 3 4 q 3 5