第四章要求 1.掌握图像的灰度变换、直方图修正、空域及频域平滑与锐化方法: 2.掌握中值滤波法及与平均滤波法的异同: 3.了解图像的彩色增强及同态增晰法。 必做题及参考答案 4.4设1幅图像具有如题表4.4.1所示概率分布,对其分别进行直方图均衡化和规定化。要求规定化后 的图像具有如题表4.4.2所示的灰度级分布。 题表4.4.1 灰度级 0 1 2 3 4 5 6 7 各灰度级概率分布 0.14 0.22 0.25 0.17 0.10 0.06 0.03 0.03 题表4.4.2 灰度级 0 1 2 3 4 5 b 7 各灰度级概率分布 0 0 0 0.19 0.25 0.21 0.24 0.11 解答: (1)直方图均衡化结果如下表所示 序 号 运 算 步骤和结果 1 列出原图像灰度级 0 1 2 3 4 5 6 7 2 各灰度级概率分布(直方图)P① 0.14 0.22 0.25 0.17 0.10 0.06 0.03 0.03 3 计算累计直方图P,=之P(k) 0.14 0.36 0.61 0.78 0.88 0.94 0.97 1.00 4 计算变换后的灰度值: 3 6 7 > j=1NT[(L-1)P,+0.5] 确定映射对应关系(→j) 0→1 1→3 2→4 3→5 4→6 5,6,7→7 6 计算新直方图PG 0 0.14 0 0.22 0.25 0.170.100.12 (2)直方图规定化结果如下表所示。 序 号 运 算 步骤和结果 1 列出图像灰度级(ⅰ或) 0 1 2 3 4 5 6 7 2 原图像各灰度级概率分布P① 0.14 0.22 0.25 0.17 0.10 0.06 0.03 0.03 3 计算原图像累计直方图P 0.14 0.36 0.61 0.78 0.88 0.94 0.97 1.00 4 规定直方图PG) 0 0 0 0.19 0.25 0.21 0.24 0.11 5 计算规定累计直方图P 0 0.19 0.44 0.65 0.89 1.00 6 按照P」→P找到i对应的j 5 6 6 7 7 7 7 确定变换关系i一j 2→5 3,4*6 5,67→7 8 求变换后的匹配直方图P) 0 0 0 0.140.22 0.250.270.12 6
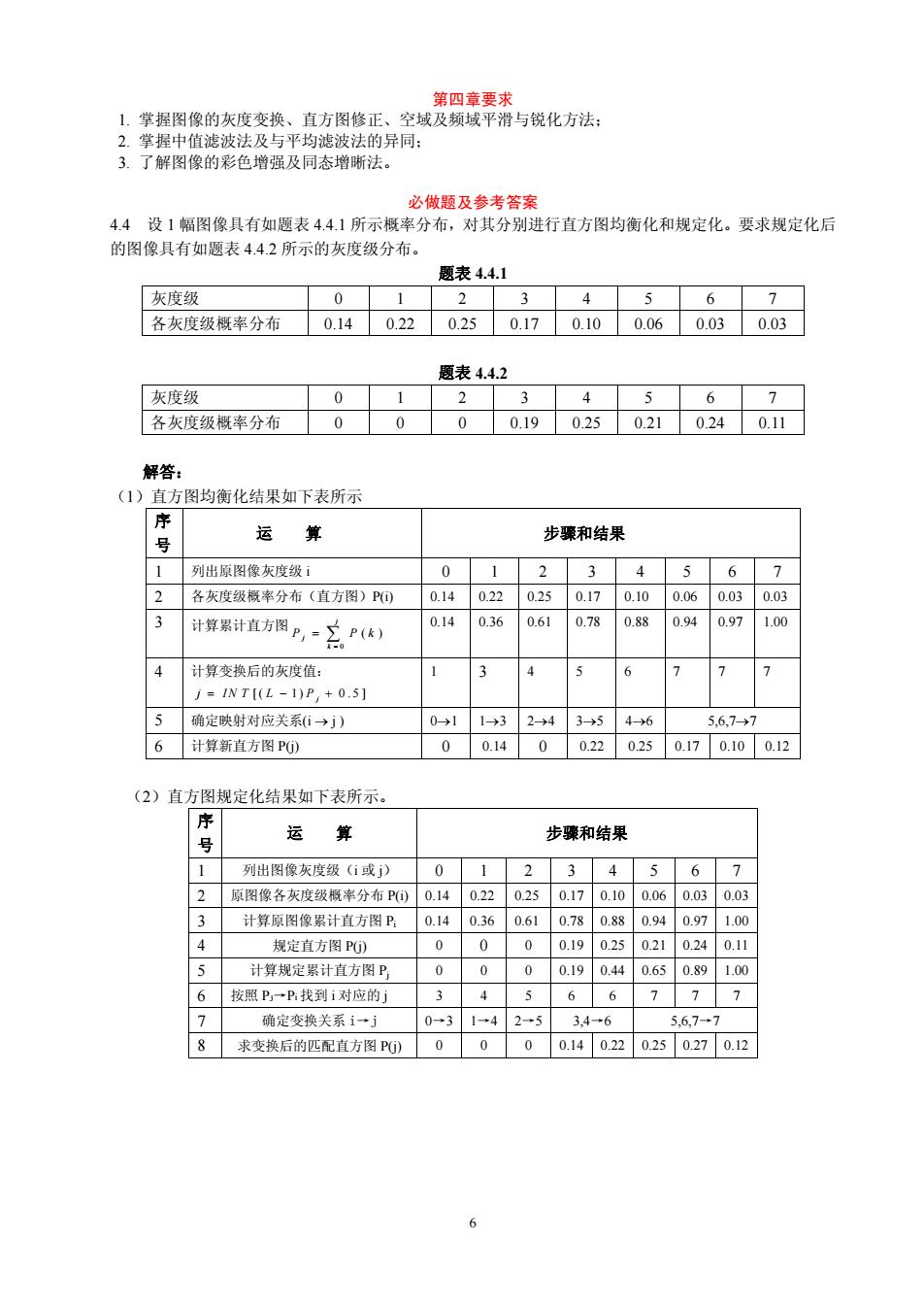
6 第四章要求 1. 掌握图像的灰度变换、直方图修正、空域及频域平滑与锐化方法; 2. 掌握中值滤波法及与平均滤波法的异同; 3. 了解图像的彩色增强及同态增晰法。 必做题及参考答案 4.4 设 1 幅图像具有如题表 4.4.1 所示概率分布,对其分别进行直方图均衡化和规定化。要求规定化后 的图像具有如题表 4.4.2 所示的灰度级分布。 题表 4.4.1 灰度级 0 1 2 3 4 5 6 7 各灰度级概率分布 0.14 0.22 0.25 0.17 0.10 0.06 0.03 0.03 题表 4.4.2 灰度级 0 1 2 3 4 5 6 7 各灰度级概率分布 0 0 0 0.19 0.25 0.21 0.24 0.11 解答: (1)直方图均衡化结果如下表所示 序 号 运 算 步骤和结果 1 列出原图像灰度级 i 0 1 2 3 4 5 6 7 2 各灰度级概率分布(直方图)P(i) 0.14 0.22 0.25 0.17 0.10 0.06 0.03 0.03 3 计算累计直方图 0 ( ) j j k P P k = = ∑ 0.14 0.36 0.61 0.78 0.88 0.94 0.97 1.00 4 计算变换后的灰度值: [( 1) 0.5] j j IN T L P = −+ 1 3 4 5 6 7 7 7 5 确定映射对应关系(i → j ) 0→1 1→3 2→4 3→5 4→6 5,6,7→7 6 计算新直方图 P(j) 0 0.14 0 0.22 0.25 0.17 0.10 0.12 (2)直方图规定化结果如下表所示。 序 号 运 算 步骤和结果 1 列出图像灰度级(i 或 j) 0 1 2 3 4 5 6 7 2 原图像各灰度级概率分布 P(i) 0.14 0.22 0.25 0.17 0.10 0.06 0.03 0.03 3 计算原图像累计直方图 Pi 0.14 0.36 0.61 0.78 0.88 0.94 0.97 1.00 4 规定直方图 P(j) 0 0 0 0.19 0.25 0.21 0.24 0.11 5 计算规定累计直方图 Pj 0 0 0 0.19 0.44 0.65 0.89 1.00 6 按照 Pj→Pi 找到 i 对应的 j 3 4 5 6 6 7 7 7 7 确定变换关系 i→j 0→3 1→4 2→5 3,4→6 5,6,7→7 8 求变换后的匹配直方图 P(j) 0 0 0 0.14 0.22 0.25 0.27 0.12

4.5设工业检测中工件的图像受到零均值、与图像不相关噪声的影响。假设图像采集装置每秒可采集30 幅图,若采用图像平均法将噪声的均方差减小到原来的1/10,则工件需固定在采集装置前多长时间? 解答: 由式(4.3.19)可知通过图像平均法可以将噪声均方差降低到原来的,√F,M为用于平均的图像个 数,所以如果 0?a,=VFo。 解得,M=100 =100/30=3.33秒 4.8对于如下所示的空域增强公式,试推导出其相应的频域等价滤波器H(,v)。 8(m,n)=f(m,n)-f(m+I,n)+f(m,n)-f(m,n+1) 解答: 对题设表达式进行傅立叶变换得 G(u,v)=F(u,v)-F(u,v)e+F(u,v)-F(u,v)e =[1-eRzN]F(u.y)+[1-eRzN]F(u.v) =[-e2M)+(1-e2】F(u,y) =H(u,v)F(u,v) 所以,频域的等价滤波器为 H(u,y)=1-e2m/M)+(1-e2mN) 4.16如题图4.16所示256×256的二值图像(白为1,黑为0),其中的白条是7像素宽,210像素高。 两个白条之间的宽度是17像素,当应用下面的方法处理时图像的变化结果(按最靠近原则仍取0或1) 是什么?(图像边界不考虑) (1)3×3的邻域平均滤波。 (2)7×7的邻域平均滤波。 (3)9×9的邻域平均滤波。 题图4.16
7 4.5 设工业检测中工件的图像受到零均值、与图像不相关噪声的影响。假设图像采集装置每秒可采集 30 幅图,若采用图像平均法将噪声的均方差减小到原来的 1/10,则工件需固定在采集装置前多长时间? 解答: 由式(4.3.19)可知通过图像平均法可以将噪声均方差降低到原来的 1 M ,M 为用于平均的图像个 数,所以如果 1 1 σ g 10σ σ n n M = = 解得,M=100 t=100/30=3.33 秒 4.8 对于如下所示的空域增强公式,试推导出其相应的频域等价滤波器 Huv (,) 。 gmn f mn f m n f mn f mn ( , ) ( , ) ( 1, ) ( , ) ( , 1) = − ++ − + 解答: 对题设表达式进行傅立叶变换得 2/ 2/ 2/ 2/ 2/ 2/ (,) (,) (,) (,) (,) 1 (,) 1 (,) [(1 ) (1 )] ( , ) (,) (,) j uM j vN j uM j vN j uM j vN Guv Fuv Fuve Fuv Fuve e Fuv e Fuv e e Fuv HuvFuv π π π π π π =− +− =− +− ⎡ ⎤⎡⎤ ⎣ ⎦⎣⎦ = − +− = 所以,频域的等价滤波器为 2/ 2/ ( , ) (1 ) (1 ) j uM j vN Huv e e π π =− +− 4.16 如题图 4.16 所示256 256 × 的二值图像(白为 1,黑为 0),其中的白条是 7 像素宽,210 像素高。 两个白条之间的宽度是 17 像素,当应用下面的方法处理时图像的变化结果(按最靠近原则仍取 0 或 1) 是什么?(图像边界不考虑) (1)3 3 × 的邻域平均滤波。 (2)7 7 × 的邻域平均滤波。 (3)9 9 × 的邻域平均滤波。 题图 4.16