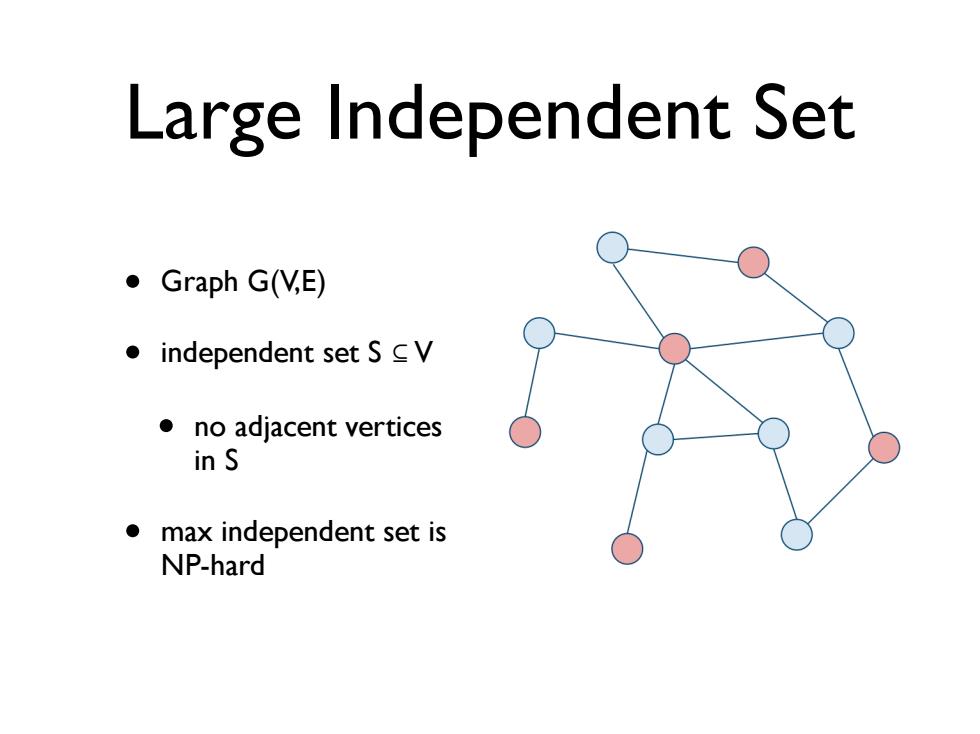
Large Independent Set ●Graph G(NE) ●independent set S CV ●no adjacent vertices inS max independent set is NP-hard
Large Independent Set • Graph G(V,E) • independent set S ⊆ V • no adjacent vertices in S • max independent set is NP-hard

Theorem G has n vertices and m edges an independent set S of size n2 4m -uniformly -sample S A uniform S is very unlikely to be an independent set!
G has n vertices and m edges ∃ an independent set S of size n2 4m Theorem uniformly sample S ? A uniform S is very unlikely to be an independent set!