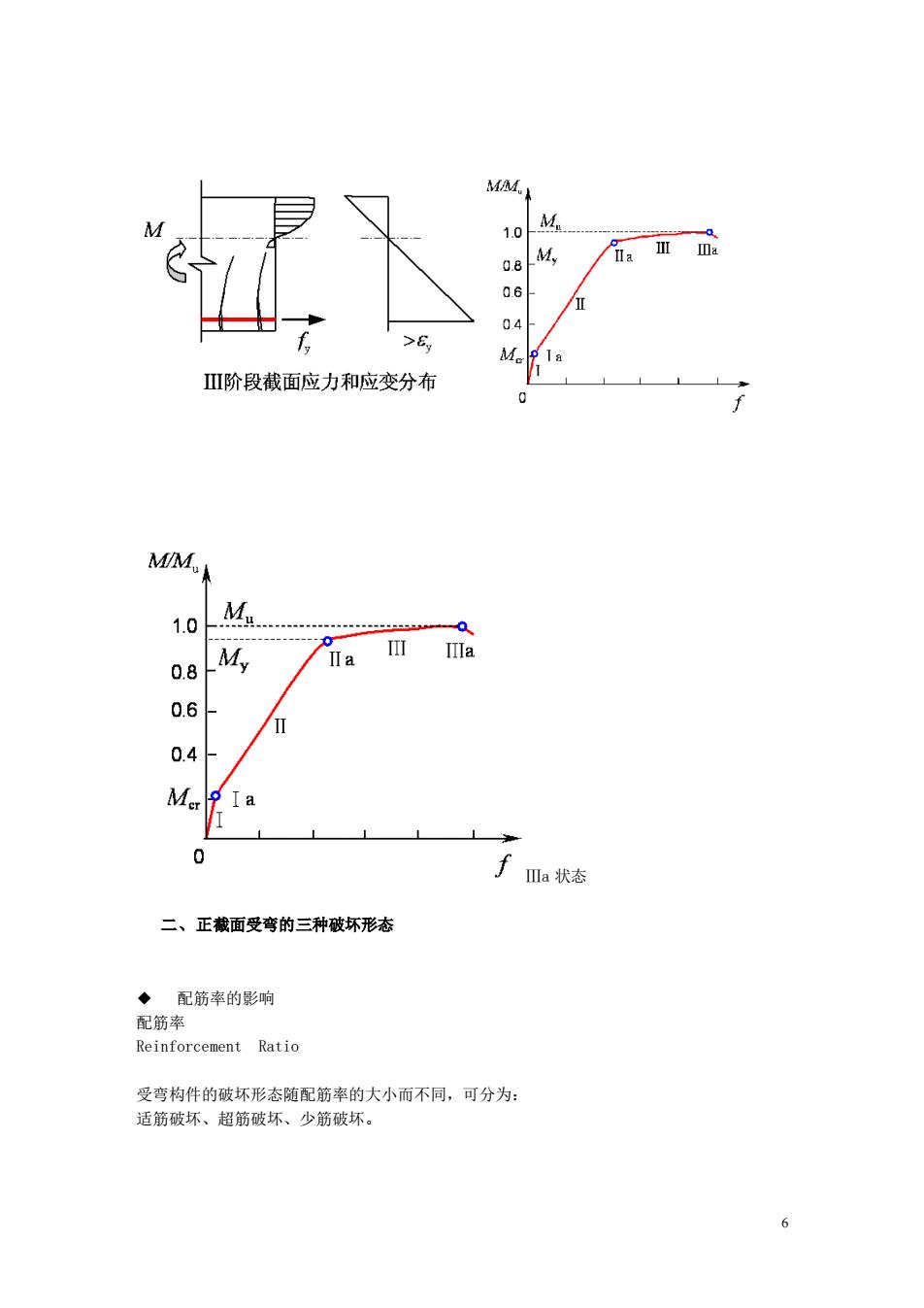
MM. 1.0 M M, Me Ⅲ阶段截面应力和应变分布 M 1.0 M 0.8 My 0.6 0, M 0 Ⅲa状态 二、正截面受弯的三种破坏形态 ◆配筋奉的影响 配筋率 Reinforcement Ratio 受弯构件的破坏形态随配筋率的大小而不同,可分为: 适筋破坏、超筋破坏、少筋破坏。 6
6 Ⅲa 状态 二、正截面受弯的三种破坏形态 ◆ 配筋率的影响 配筋率 Reinforcement Ratio 受弯构件的破坏形态随配筋率的大小而不同,可分为: 适筋破坏、超筋破坏、少筋破坏
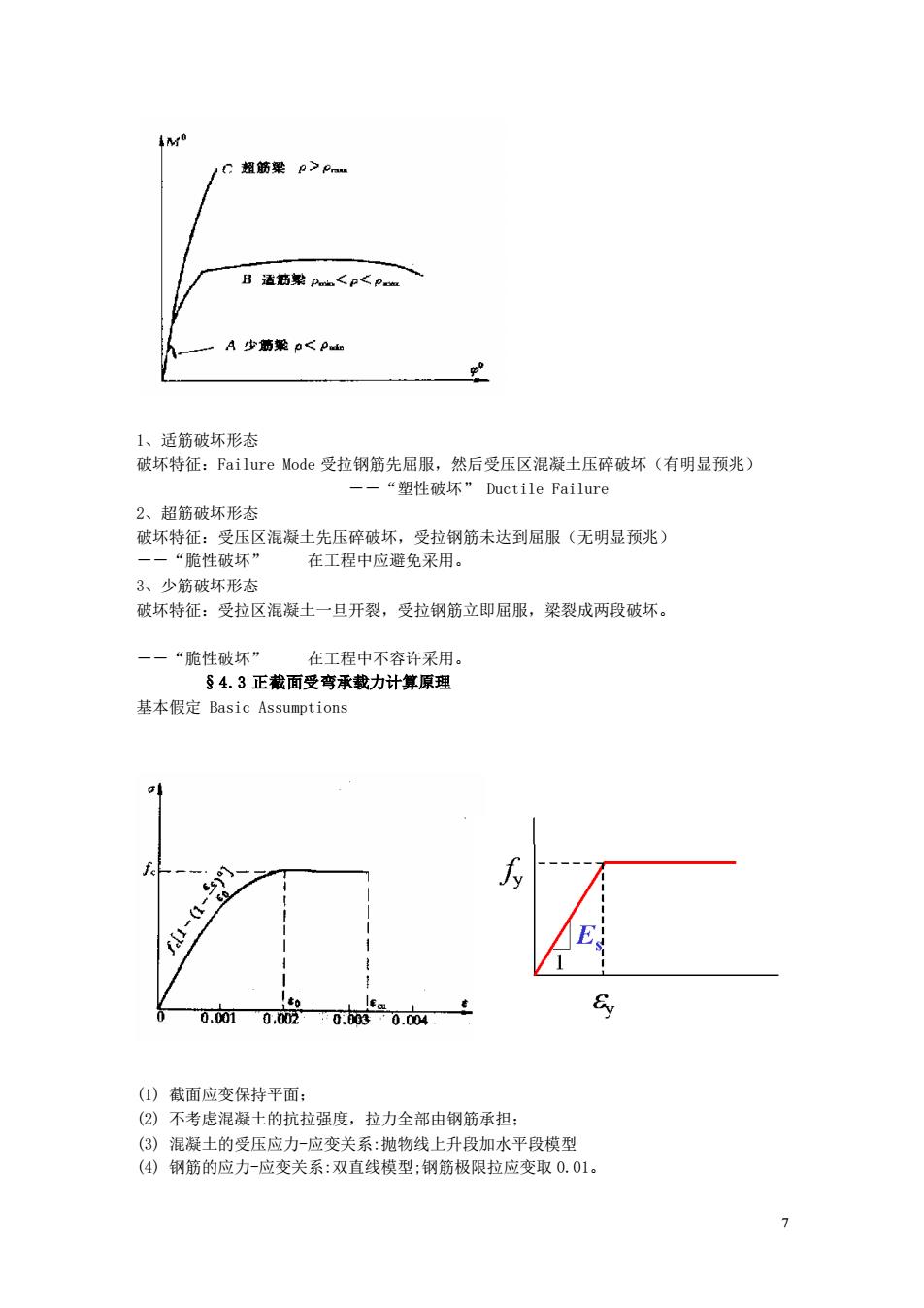
/C超筋粱p>e- B适商第A<P<P A少声粱p<P山 1、适筋破坏形态 破坏特征:Failure Mode受拉钢筋先屈服,然后受压区混凝士压碎破坏(有明显预兆) ,“塑性破坏”Ductile Failure 2、超筋破坏形态 破坏特征:受压区混凝土先压碎破坏,受拉钢筋未达到屈服(无明显预兆) 一“暗性破坏” 在工程中应避免采用。 3、少筋破坏形态 破坏特征:受拉区混凝士一旦开裂,受拉钢筋立即屈服,梁裂成两段破坏。 一一“脆性破坏” 在工程中不容许采用。 §4.3正截面受弯承载力计算原理 基本假定Basic Assumptions 0.0.0 0ts0.4 (1)截面应变保持平面: (②)不考虑混凝士的抗拉强度,拉力全部由钢筋承担: (③)混凝土的受压应力-应变关系:抛物线上升段加水平段模型 (4)钢筋的应力-应变关系:双直线模型:钢筋极限拉应变取0.01
7 1、适筋破坏形态 破坏特征:Failure Mode 受拉钢筋先屈服,然后受压区混凝土压碎破坏(有明显预兆) --“塑性破坏” Ductile Failure 2、超筋破坏形态 破坏特征:受压区混凝土先压碎破坏,受拉钢筋未达到屈服(无明显预兆) --“脆性破坏” 在工程中应避免采用。 3、少筋破坏形态 破坏特征:受拉区混凝土一旦开裂,受拉钢筋立即屈服,梁裂成两段破坏。 --“脆性破坏” 在工程中不容许采用。 §4.3 正截面受弯承载力计算原理 基本假定 Basic Assumptions (1) 截面应变保持平面; (2) 不考虑混凝土的抗拉强度,拉力全部由钢筋承担; (3) 混凝土的受压应力-应变关系:抛物线上升段加水平段模型 (4) 钢筋的应力-应变关系:双直线模型;钢筋极限拉应变取 0.01
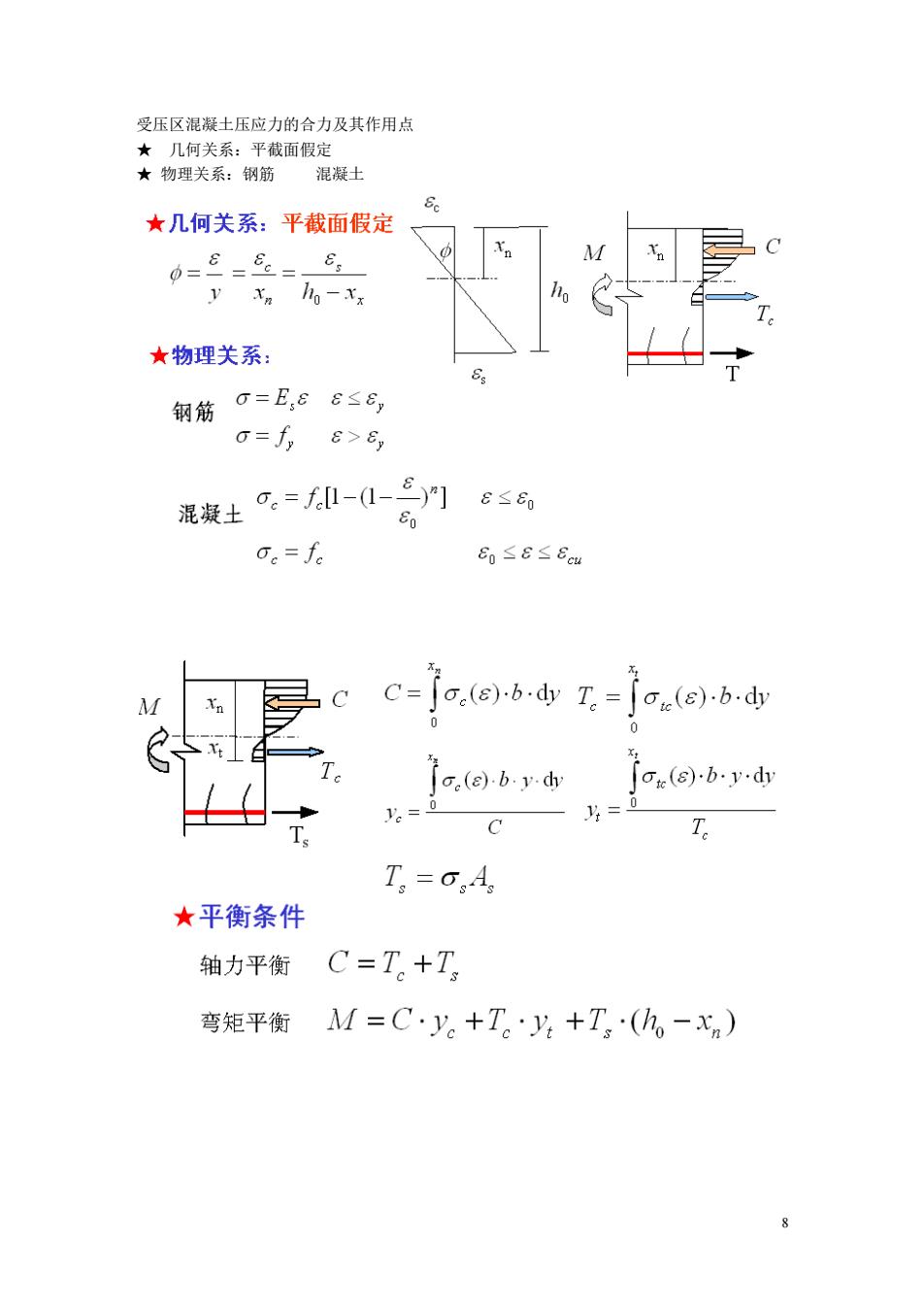
受压区混凝士压应力的合力及其作用点 几何关系:平截面假定 ★物理关系:钢筋 混凝士 ★几何关系:平截面假定 E; yxn。-x ★物理关系 钢筋0=E,88≤S 0=f8>6, 混凝土.=-1-三9]6≤ o。=f 60≤8≤8u C= (s)6.dy T=[(s).b.dy e(e).b.y.dy 「o(8)by.d 17 T T=0:A ★平衡条件 轴力平衡C=T。+T 弯矩平衡M=C·y。+T。片+T,(h。-xn) 8
8 受压区混凝土压应力的合力及其作用点 ★ 几何关系:平截面假定 ★ 物理关系:钢筋 混凝土