
同理,=12的不同原子核,因磁矩不同,即使 在同一外加磁场强度下,发生核跃迁时需要的能量也 是不同的。例如氟核磁矩(F)<(H),故在同一 外加磁场强度下发生核跃迁时,氢核需要的能量将高· 于氟核 哈潮清月掌大是 HARBIN LNTVERSTTY OF COMMERCE
同理,I=1/2的不同原子核,因磁矩不同,即使 在同一外加磁场强度下,发生核跃迁时需要的能量也 是不同的。例如氟核磁矩(μF)<(μH),故在同一 外加磁场强度下发生核跃迁时,氢核需要的能量将高 于氟核
5.2.3核的回旋 当原子核的核磁矩处于外加磁场B0中,由于核自 身的旋转,而外加磁场又力求它取向于磁场方向,在 ·这两种力的作用下,°核会在自旋的同时绕外磁场的方 向进行回旋,这种运动称为Larmor进动。 AB Bo 回旋轴-→ 核磁距μ 回旋轴 ←一一自旋轴 自旋轴 核磁距μ m=+1/2 m=-1/2 哈蘭演第大孕 HARBIN LNTVERSITY OP COMMERCE
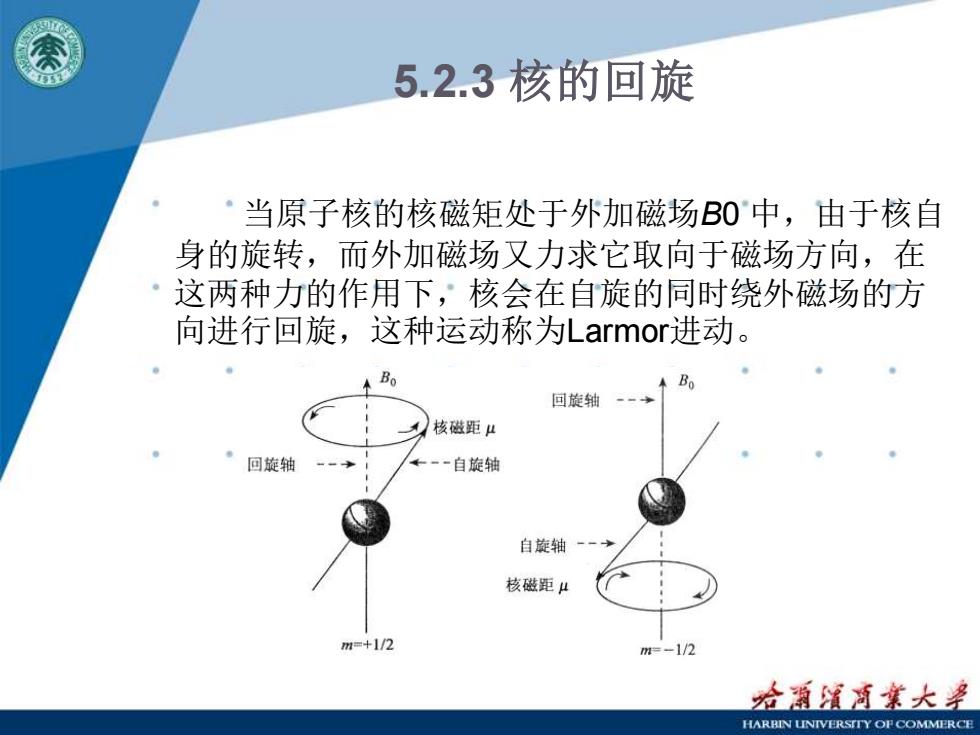
5.2.3 核的回旋 当原子核的核磁矩处于外加磁场B0 中,由于核自 身的旋转,而外加磁场又力求它取向于磁场方向,在 这两种力的作用下,核会在自旋的同时绕外磁场的方 向进行回旋,这种运动称为Larmor进动

原子核在磁场中的回旋,这种现象与一个自旋的陀 螺与地球重力线做回旋的情况相似。 换句话说:由于磁场的作用,原子核一方面绕轴 自旋,另一方面自旋轴又围绕着磁场方向进动。其进 ·动频率,除与原子核本身特征有关外,还与外界的磁 场强度有关。进动时的频率、自旋质点的角速度与外 。加磁场的关系可用Larmor方程表示: W=2TTV=yBo (10.4) V=Y/2πBo (10.5) 式中:ω一角速度;V一 进动频率(回旋频率); Y一旋磁比(特征性常数) 疮源商拿大是 HARBIN LNTVERSTTY OF COMMERCE
原子核在磁场中的回旋, 这种现象与一个自旋的陀 螺与地球重力线做回旋的情况相似。 换句话说:由于磁场的作用,原子核一方面绕轴 自旋,另一方面自旋轴又围绕着磁场方向进动。其进 动频率,除与原子核本身特征有关外,还与外界的磁 场强度有关。进动时的频率、自旋质点的角速度与外 加磁场的关系可用Larmor方程表示: ω = 2 π v = γ B0 (10.4) v = γ / 2π B0 (10.5) 式中:ω— 角速度;v — 进动频率(回旋频率); γ— 旋磁比(特征性常数)

由Larmor方程表明,自旋核的进动频率与外加磁 场强度成正比。当外加磁场强度B。增加时,核的回旋 角速度增大,其回旋频率也增加。对H核来说,当磁 场强度B为1.4092T(1T=104)高斯时,所产生的回旋频 率v为60兆赫(y=26.753×107radT-1.s1);B,为 ,2.3487T高斯时,所产生的回旋频率v为100兆赫。 给雨渭商業大孕 HARBIN LNTVERSITY OP COMMERCE
由Larmor方程表明,自旋核的进动频率与外加磁 场强度成正比。当外加磁场强度B0 增加时,核的回旋 角速度增大,其回旋频率也增加。对1H核来说,当磁 场强度B0为1.4092T(1T=104 )高斯时,所产生的回旋频 率v为60兆赫(γ =26. 753×107 rad·T−1·s−1);B0为 2.3487T高斯时,所产生的回旋频率v为100兆赫

第二节核磁共振波谱仪 仪器原理及组成 我们知道,实现NMR即满足核跃迁的条件 是:. △E(核跃迁能)=△E (辐射能) 即· 2uB0 h v 给潮清月掌大呈 HARBIN LNTVERSTTY OF COMMERCE
第二节 核磁共振波谱仪 一、 仪器原理及组成 我们知道,实现NMR即满足核跃迁的条件 是: △E(核跃迁能)= △E,(辐射能) 即 2μB0 = h v