
二、几何均数 1、,几何均数(geometric mean,简记为G)指 将个变量值仪1,X2,X3 .,Xn)的乘积 开n次方。用G表示其平均水平。 2、适用条件:对于变量值呈倍数或等比关系、 或呈对数正态分布(正偏态分布)的资料。如抗 体效价及抗体滴度,某些传染病的潜伏期,细 菌计数等。 3、计算公式:有直接法和加权法。 简历 返回总目录返回章耳录口>口结束 第2章定量资料的统计描述 第20页
简 历 返回总目录 返回章目录 结束 第2章 定量资料的统计描述 第20页 1、几何均数(geometric mean,简记为G):指 将n个变量值(X1 ,X2 ,X3 ,.,Xn)的乘积 开n次方。用G表示其平均水平。 2、适用条件:对于变量值呈倍数或等比关系、 或呈对数正态分布(正偏态分布)的资料。如抗 体效价及抗体滴度,某些传染病的潜伏期,细 菌计数等。 3、计算公式:有直接法和加权法。 二、几何均数
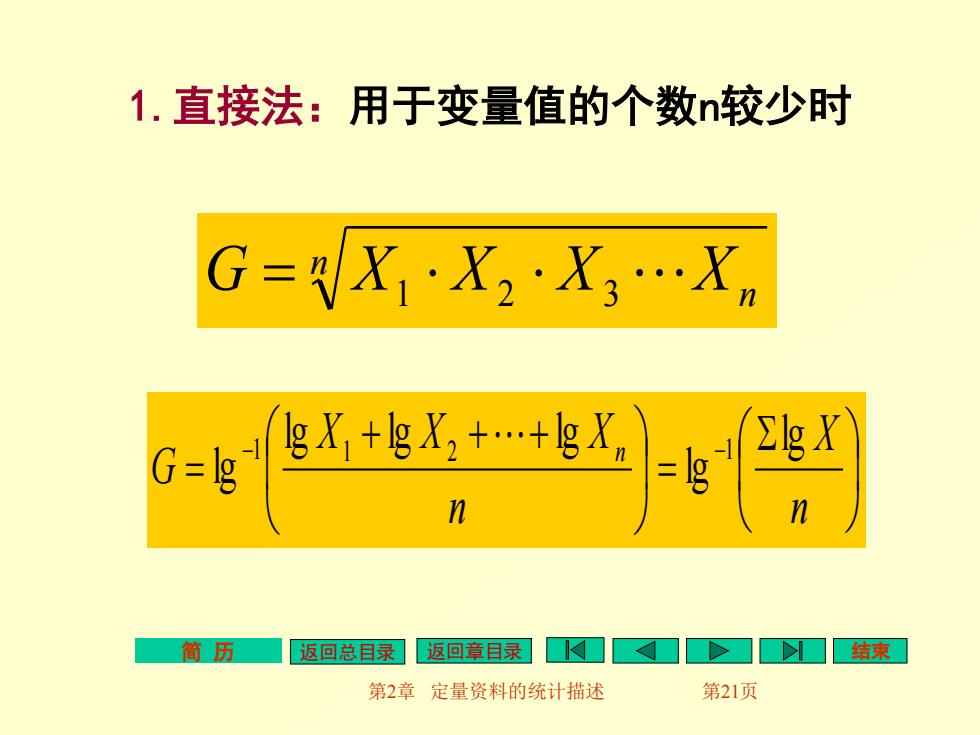
1.直接法:用于变量值的个数n较少时 G=X1X2·X,.Xm G=lg gX1+gX2+.+gXn =lg 简历 返回总目录]返回章目录口>口结束 第2章定量资料的统计描述 第21页
简 历 返回总目录 返回章目录 结束 第2章 定量资料的统计描述 第21页 1.直接法:用于变量值的个数n较少时 n G X1 X2 X3 Xn = = + + + = − − n X n X X X G n lg lg lg lg lg lg 1 1 2 1

直接法计算实例 G=/2×4×8×16×32×64=11.31 G=lg lg 2+1g 4+1g 8+1g 16+lg 32+1g 64 =lg11.0536=11.31 6 简历 返回总目绿 返回章耳录4口>]口结束 第2章定量资料的统计描述 第22页
简 历 返回总目录 返回章目录 结束 第2章 定量资料的统计描述 第22页 2 4 8 16 32 64 11.31 6 G = = lg 1.0536 11.31 6 lg 2 lg 4 lg 8 lg16 lg 32 lg 64 lg 1 1 = = + + + + + = − − G 直接法计算实例
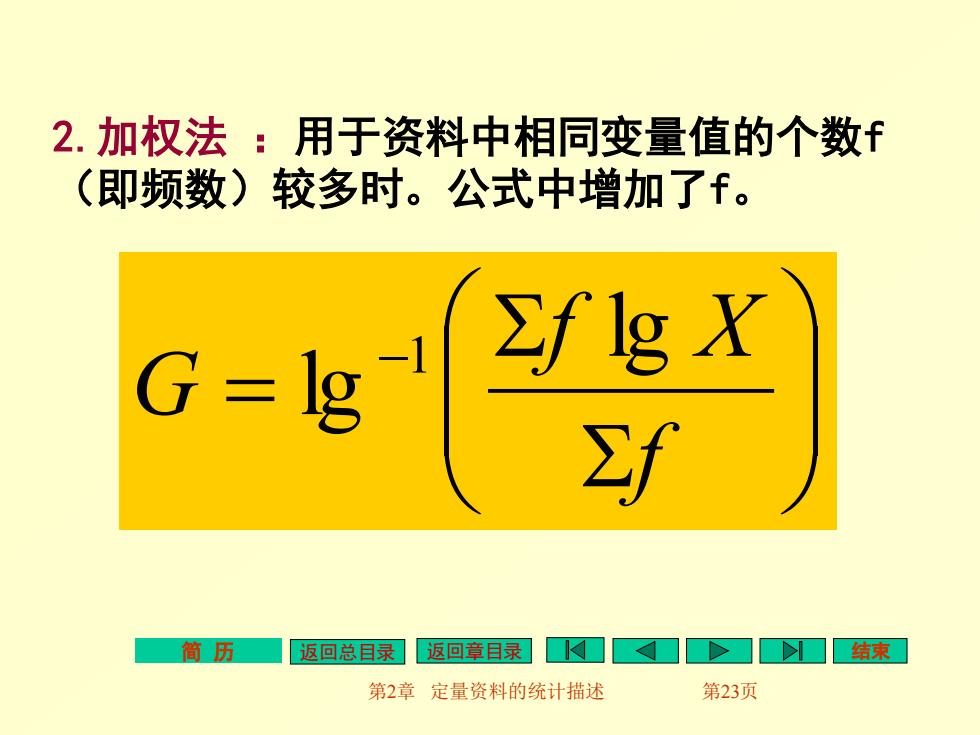
2.加权法:用于资料中相同变量值的个数f (即频数)较多时。公式中增加了f。 G=lg >flg X 2f 简历 返回总目录返回章目录口>口结束 第2章定量资料的统计描述 第23页
简 历 返回总目录 返回章目录 结束 第2章 定量资料的统计描述 第23页 2.加权法 :用于资料中相同变量值的个数f (即频数)较多时。公式中增加了f。 = − f f X G lg lg 1
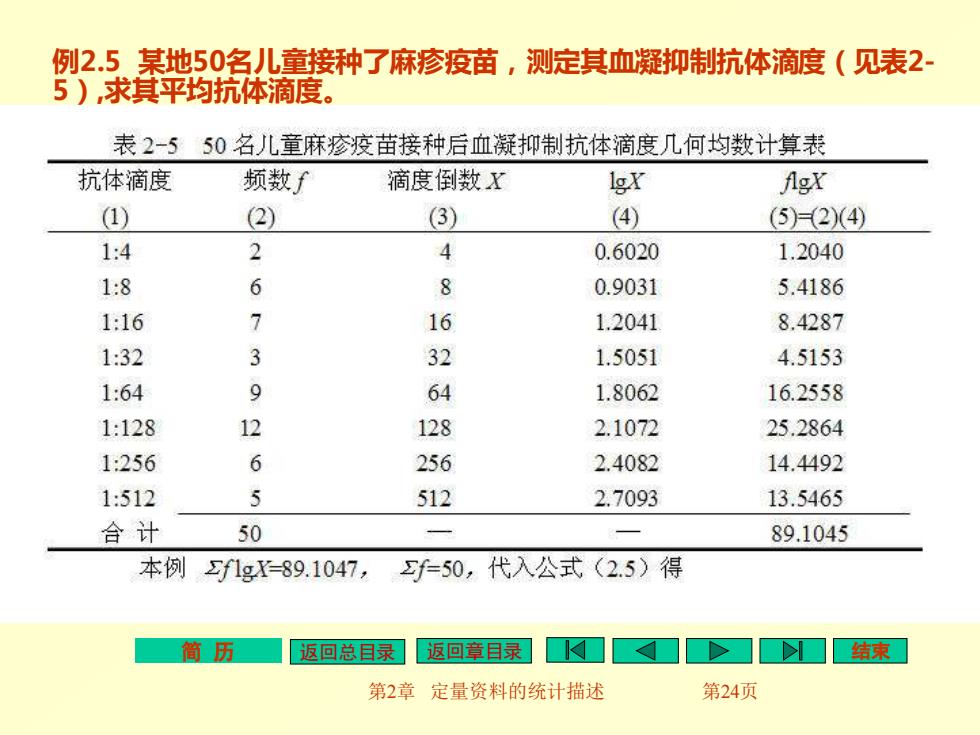
例2.5某地50名儿童接种了麻疹疫苗,测定其血凝抑制抗体滴度(见表2- 5),求其平均抗体滴度。 表2-550名儿童麻疹疫苗接种后血凝抑制抗体滴度几何均数计算表 抗体滴度 频数f 滴度倒数X laY AgY (1) (2) (3) (4) (5)=(2)(4) 1:4 2 4 0.6020 1.2040 1:8 6 8 0.9031 5.4186 1:16 7 16 1.2041 8.4287 1:32 3 32 1.5051 4.5153 1:64 9 64 1.8062 16.2558 1:128 12 128 2.1072 25.2864 1:256 6 256 2.4082 14.4492 1:512 5 512 2.7093 13.5465 合计 50 89.1045 本例f1g-89.1047, f=50,代入公式(2.5)得 简历 返回总目录 返回章目录 >i 结束 第2章定量资料的统计描述 第24页
简 历 返回总目录 返回章目录 结束 第2章 定量资料的统计描述 第24页 例2.5 某地50名儿童接种了麻疹疫苗,测定其血凝抑制抗体滴度(见表2- 5),求其平均抗体滴度