
运动方程写为?-w2= m dv k dt dv m 因=0时,0=0;并设时,速度为0.取定积分 则有= = x 4+x +C 2a UtD k I= g t v/m's-1 20 UT -U m 60 V-54m.s1 28i 28t 40 UT e -1 1-e UT 20 U=UT 三UT 28t ts 0510152025 Tt+ e 1+e oT t 设m=70kg,Ur=54ms-1, 则k=0.24N2m2g 可得到如图所示的)函数曲线
------------------------------------------------------------------------------- 运动方程写为 dt d k m T − = 2 2 dt m d k T = − 2 2 因t=0时,=0;并设t时,速度为 . 取定积分 则有 = − t T dt m d k 0 0 2 2 c a x a x a x a dx + − + = − ln 2 1 2 2 t m k T T T = − + ln 2 1 t g T 2 = 1 1 2 2 + − = t t g T t T g T e e t t g T t T g T e e 2 1 1 2 − + − = − 设m=70 kg, T=54 m·s-1,则k=0.24 N2·m2·s-1. 可得到如图所示的(t)函数曲线
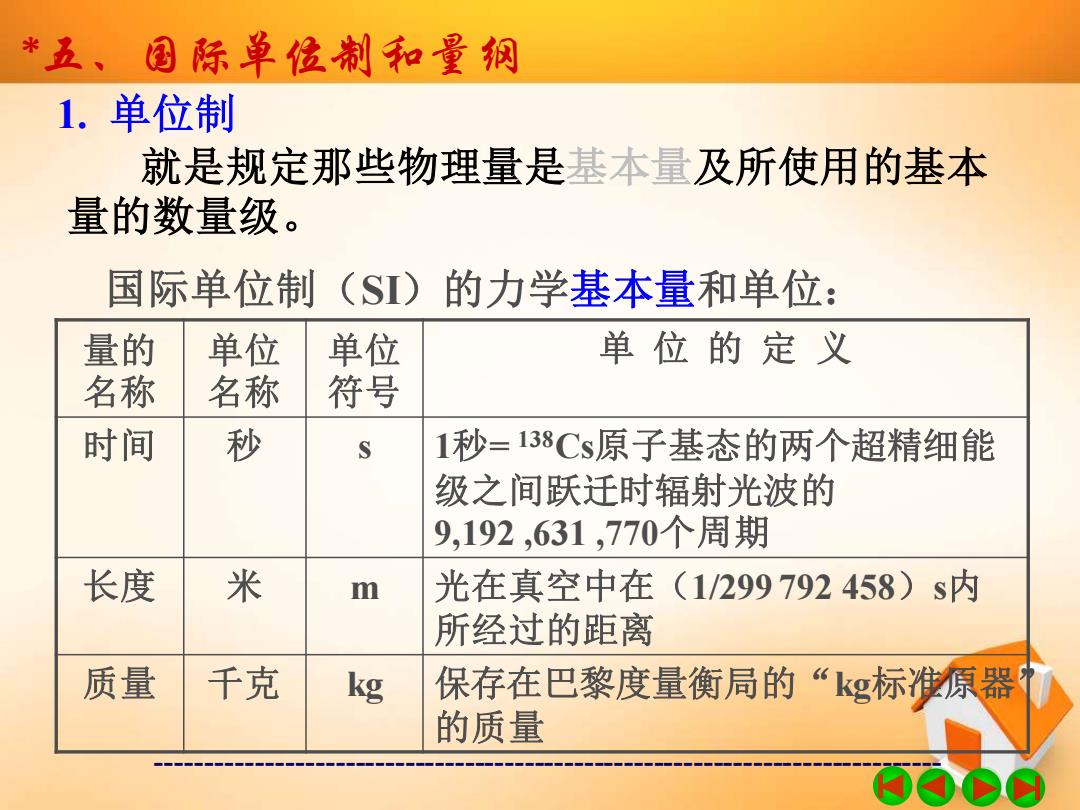
*五、国际单位制和量纲 1.单位制 就是规定那些物理量是基本量及所使用的基本 量的数量级。 国际单位制(S)的力学基本量和单位: 量的 单位 单位 单位的定义 名称 名称 符号 时间 秒 S 1秒=138Cs原子基态的两个超精细能 级之间跃迁时辐射光波的 9,192,631,770个周期 长度 米 m 光在真空中在(1/299792458)s内 所经过的距离 质量 千克 kg 保存在巴黎度量衡局的“kg标准原器 的质量
------------------------------------------------------------------------------- *五、国际单位制和量纲 1. 单位制 就是规定那些物理量是基本量及所使用的基本 量的数量级。 量的 名称 单位 名称 单位 符号 单 位 的 定 义 时间 秒 s 1秒= 138Cs原子基态的两个超精细能 级之间跃迁时辐射光波的 9,192 ,631 ,770个周期 长度 米 m 光在真空中在(1/299 792 458)s内 所经过的距离 质量 千克 kg 保存在巴黎度量衡局的“kg标准原器” 的质量 国际单位制(SI)的力学基本量和单位:

2.量纲 可根据一定的关系式,从基本量导出的量称为导 出量,相应的单位称为导出单位。 为定性表示导出量和基本量间的关系,常不考虑 关系式中的数字因数,而将物理量用若干基本量的乘 方之积表示,这样的式子称为该物理量的量纲式,简 称量纲。 某物理量Q的量纲通常表示为[Q]。 在SI中,基本力学量是长度、质量、时间,它们的 量纲分别用L、M、T表示
------------------------------------------------------------------------------- 2. 量纲 可根据一定的关系式,从基本量导出的量称为导 出量,相应的单位称为导出单位。 为定性表示导出量和基本量间的关系,常不考虑 关系式中的数字因数,而将物理量用若干基本量的乘 方之积表示,这样的式子称为该物理量的量纲式,简 称量纲。 某物理量 Q 的量纲通常表示为 Q 。 在SI中,基本力学量是长度、质量、时间,它们的 量纲分别用 L、M、T 表示

例如:在SI制中 w=1g1=1八 [a]=LT-2 [F]=MLT-2 只有量纲相同的项才能进行加减或用等式联接。 QOOA
------------------------------------------------------------------------------- 例如:在SI制中 −1 = = LT dt ds [] [ ] −2 [a] = LT F = MLT−2 只有量纲相同的项才能进行加减或用等式联接

§2.2动量动量守恒定律 整个物理学大厦的基石,三大守恒定律: 动量守恒定律 能量转换与守恒 角动量守恒 一,质点的动量定理 定义: 质点的动量一p=m5 △状态矢量 △相对量 定义: 力的冲量一7=F.dt
------------------------------------------------------------------------------- §2.2 动量 动量守恒定律 整个物理学大厦的基石,三大守恒定律: 动量守恒定律 能量转换与守恒 角动量守恒 一.质点的动量定理 定义: 质点的动量— p = m △ 状态矢量 △ 相对量 定义: 力的冲量 — I F dt t t = 0