
§6-5自感和互感 第六章电磁感应 复习 感应电动势的计算:法拉第电磁感应定律 dΦ :=-N dt 负号表方向,通常用楞次定律来判断。使 用时,也可以大小和方向分开讨论。 动生电动势的另一种计算方法: c=∫(⑦×B)-dl 上页 下页 返回 帮助
第六章 电磁感应 上页 下页 返回 帮助 §6-5 自感和互感 i d d Φ N t = − 动生电动势的另一种计算方法: 复习 感应电动势的计算:法拉第电磁感应定律 负号表方向,通常用楞次定律来判断。使 用时,也可以大小和方向分开讨论 。 i ( ) d L = B l v

§6-5自感和互感 第六章电磁感应 一、自感 1.自感现象 由于回路中电流变化而在回路自身中引起感 应电动势的现象,称为自感现象。由此引起的 电动势称为自感电动势。 上页 下页 返回 帮助
第六章 电磁感应 上页 下页 返回 帮助 §6-5 自感和互感 一、自感 1.自感现象 由于回路中电流变化而在回路自身中引起感 应电动势的现象,称为自感现象。由此引起的 电动势称为自感电动势

§6-5自感和巨感 第六章电磁感应 2.自感系数 穿过闭合电流回路的磁通量 Φo∝I 若线圈有N匝 w=WΦ 自感系 磁 w=WΦocI y=LI Joseph Henry (4799-1878) 单位:1亨利(H)=1韦伯/安培(1Wb/A) 1mH=10-3H,1uH=10-6H 上页 下页 返回 帮助
第六章 电磁感应 上页 下页 返回 帮助 §6-5 自感和互感 2.自感系数 穿过闭合电流回路的磁通量 Φ I 若线圈有 N 匝 = NΦ 磁 链 = NΦ I = LI 自感系 数 单位:1 亨利 ( H )= 1 韦伯 / 安培 (1 Wb / A) 1mH 10 H, 1μ H 10 H −3 −6 = =

§6-5自感和互感 第六章电磁感应 影响自感系数的因素 线圈自身的性质(如线圈形状、大小及匝数); 线圈周围介质。 3.自感电动势 dt dL d 当L为一恒量时 =0 ,则 dt dt 负号表明,自感电动势将反抗回路中电流的变 化。即当电流增加时,自感电动势与原来电流的方 向相反,当电流减小时,自感电动势与原来电流的 方向相同。这种性质被称为电磁惯性。 上页 下页 返回 帮助
第六章 电磁感应 上页 下页 返回 帮助 §6-5 自感和互感 ① 线圈自身的性质(如线圈形状、大小及 匝数); ② 线圈周围介质。 3.自感电动势 0 d d = t L t I L L d d = − ) d d d d ( d d t L I t I L t L = − = − + 影响自感系数的因素 负号表明,自感电动势将反抗回路中电流的变 化。即当电流增加时,自感电动势与原来电流的方 向相反,当电流减小时,自感电动势与原来电流的 方向相同。这种性质被称为电磁惯性。 当L为一恒量时 ,则
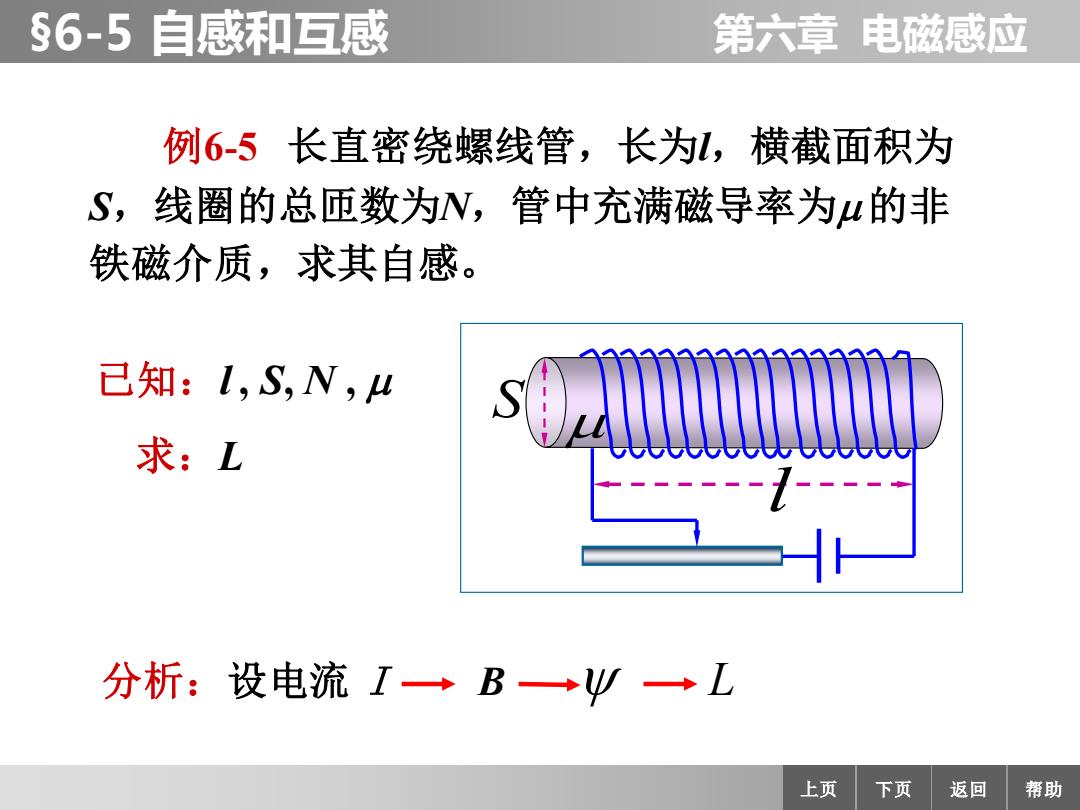
§6-5自感和互感 第六章电磁感应 例65长直密绕螺线管,长为L,横截面积为 S,线圈的总匝数为N,管中充满磁导率为4的非 铁磁介质,求其自感。 已知:I,S,N,u 求:L 分析:设电流I→B→W→L 上页 下页 返回 帮助
第六章 电磁感应 上页 下页 返回 帮助 §6-5 自感和互感 例6-5 长直密绕螺线管,长为l,横截面积为 S,线圈的总匝数为N,管中充满磁导率为 的非 铁磁介质,求其自感。 l S 已知:l , S, N , 求:L 分析:设电流 I B L