
振动是一种普遍的运动形式 机械振动:物体在某固定位置附近的往复运动, 是物体一种普遍的运动形式 广义振动:任何一个物理量在某一量值附近随 时间作周期性变化. 振动分类 受迫振动 共振 振动 (自由振动 阻尼自由振动 无阻尼自由非谐振动 无阻尼自由振动 无阻尼自由谐振动 (简谐振动)
------------------------------------------------------------------------------- 振动是一种普遍的运动形式 机械振动: 物体在某固定位置附近的往复运动, 是物体一种普遍的运动形式 . 广义振动:任何一个物理量在某一量值附近随 时间作周期性变化. 振动分类 振动 受迫振动 自由振动 共振 阻尼自由振动 无阻尼自由振动 无阻尼自由非谐振动 无阻尼自由谐振动 (简谐振动)

§10.1简谐振动的动力学特征 振动中最简单最基本的是简谐振动 简谐振动: 一个做往复运动的物体,如果其偏离平衡位置 的位移x(或角位移0随时间按余弦(或正弦)规律变 化的振动 x=Acos(@t+go) 运动学方程 x可作广义理解: 位移、电流、场强、温度. 雨的南网
------------------------------------------------------------------------------- §10.1 简谐振动的动力学特征 振动中最简单最基本的是简谐振动 简谐振动: 一个做往复运动的物体,如果其偏离平衡位置 的位移x(或角位移)随时间t按余弦(或正弦)规律变 化的振动 x=Acos(t+0 ) 运动学方程 x 可作广义理解: 位移、电流、场强、温度…
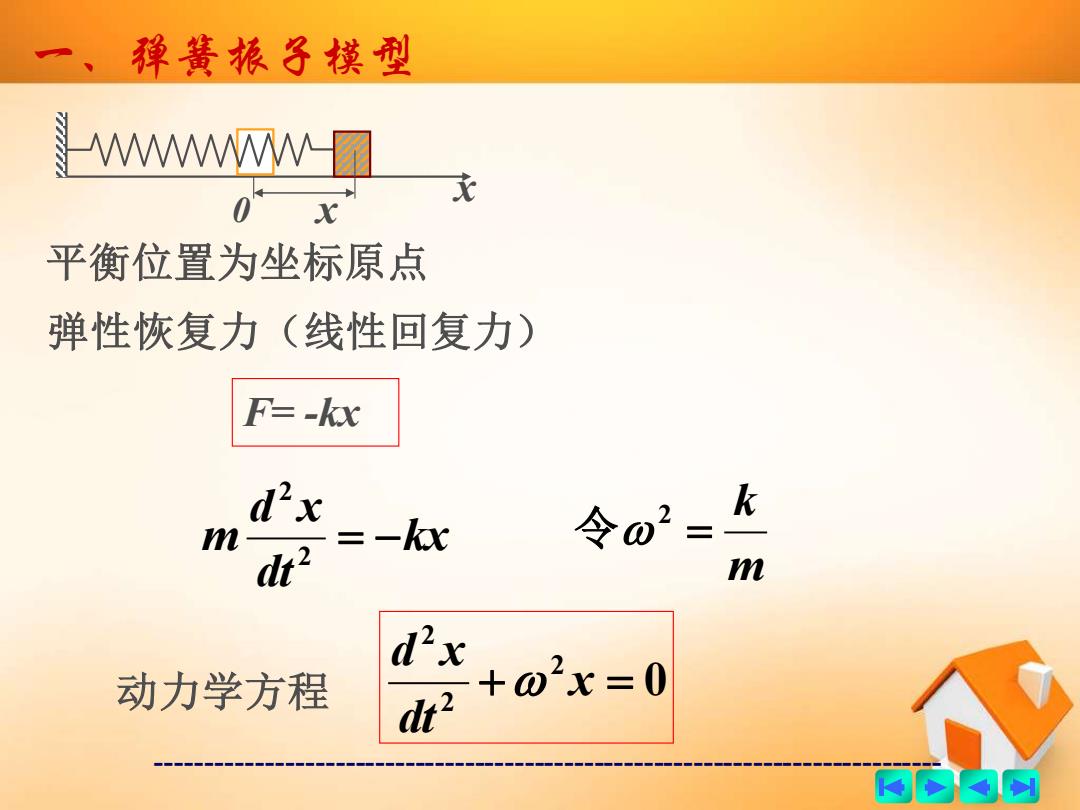
一、弹簧振子模型 WWWW-圈 平衡位置为坐标原点 弹性恢复力(线性回复力) F=-kx d2x 令02= k n =- m d2x 动力学方程 2+o2x=0 商的内网
------------------------------------------------------------------------------- x 0 x 一、弹簧振子模型 平衡位置为坐标原点 弹性恢复力(线性回复力) F= -kx kx dt d x m = − 2 2 m k = 2 令 动力学方程 0 2 2 2 + x = dt d x
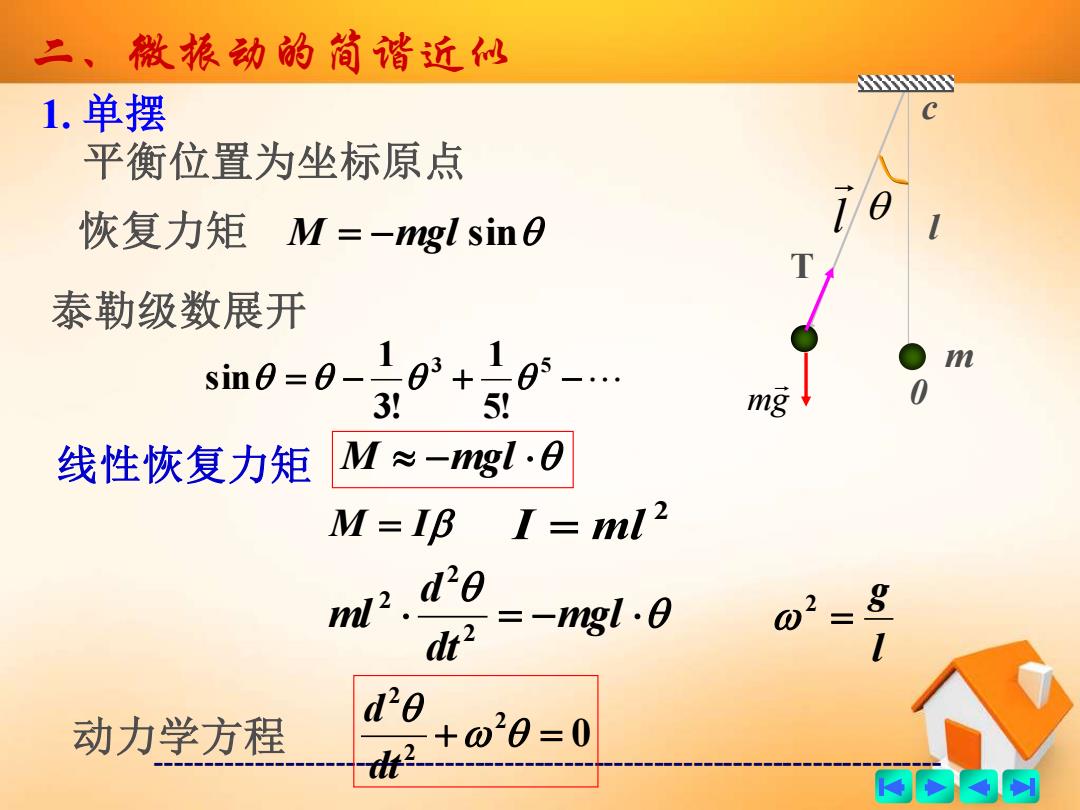
二、微振动的简谐近仙 S 1.单摆 平衡位置为坐标原点 恢复力矩M=-ngl sin0 泰勒级数展开 sin0=-10+9-… m 3! 5 mg 0 线性恢复力矩 M≈-gl.B M=I8 I=ml2 w2.120 =-g10 02 8 d20 动力学方程 +020=0 的南厨
------------------------------------------------------------------------------- 二、微振动的简谐近似 1. 单摆 c 0 mg l m T l 平衡位置为坐标原点 恢复力矩 M = −mgl sin 泰勒级数展开 = − 3 + 5 − 5! 1 3! 1 sin 线性恢复力矩 M −mgl M = I 2 I = ml = −mgl dt d ml 2 2 2 l g = 2 动力学方程 0 2 2 2 + = dt d
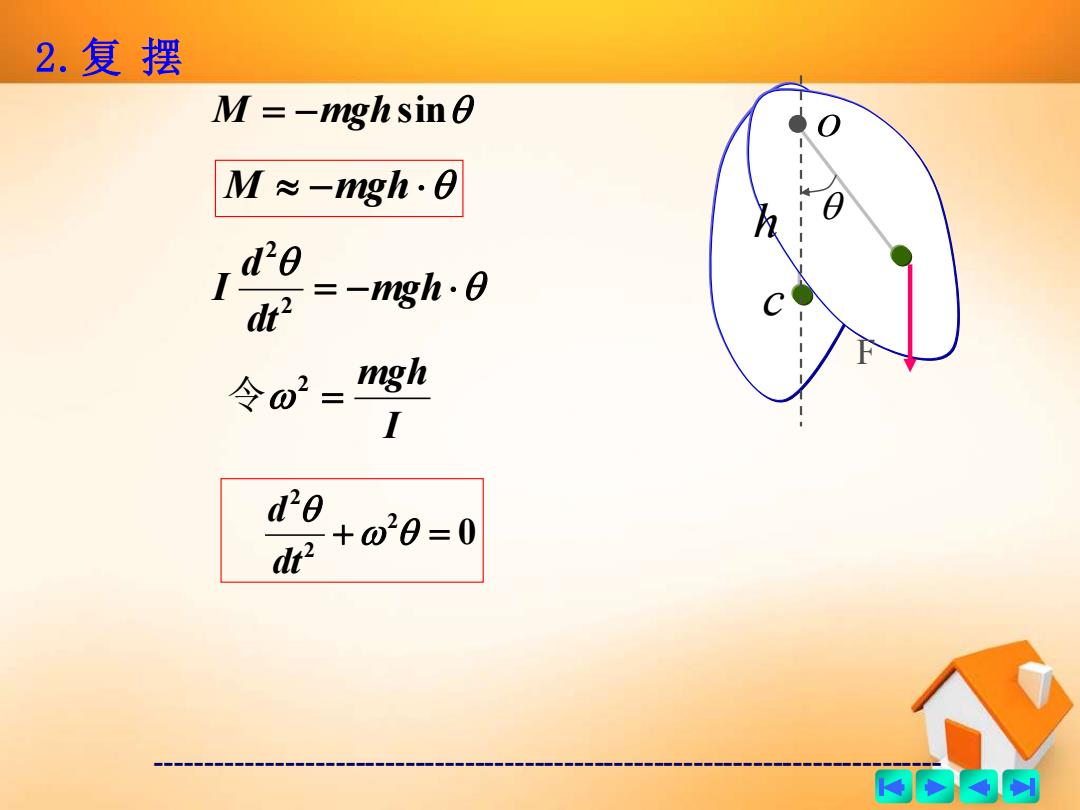
2.复摆 M=-mgh sin0 M≈-gh·B 牌g 令o2= mgh de d +020=0 商的内网
------------------------------------------------------------------------------- 2.复 摆 F c o h M = −mghsin M −mgh = −mgh dt d I 2 2 I mgh = 2 令 0 2 2 2 + = dt d