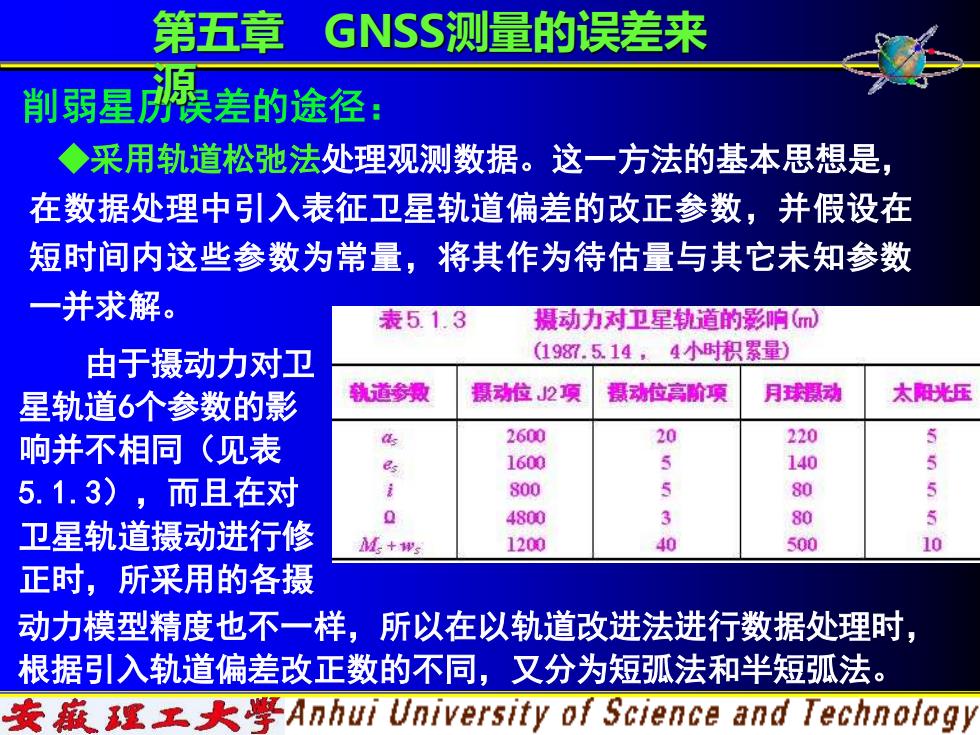
第五章 GNSS测量的误差来 削弱星晨差的途径: ◆采用轨道松驰法处理观测数据。这一方法的基本思想是, 在数据处理中引入表征卫星轨道偏差的改正参数,并假设在 短时间内这些参数为常量,将其作为待估量与其它未知参数 一并求解。 表5.1.3 摄动力对卫星轨道的影响m) 由于摄动力对卫 (1987.5.14,4小时积累量) 星轨道6个参数的影 轨道参数 摄动位J2项 蹑动位高阶项 月球摄动 太阳光压 响并不相同(见表 2600 20 220 es 1600 5 140 5 5.1.3),而且在对 800 5 80 5 4800 3 80 5 卫星轨道摄动进行修 M+ws 1200 40 500 10 正时,所采用的各摄 动力模型精度也不一样,所以在以轨道改进法进行数据处理时, 根据引入轨道偏差改正数的不同,又分为短弧法和半短弧法。 安藏理工大学Anhui University of Science and Technology
◆采用轨道松弛法处理观测数据。这一方法的基本思想是, 在数据处理中引入表征卫星轨道偏差的改正参数,并假设在 短时间内这些参数为常量,将其作为待估量与其它未知参数 一并求解。 削弱星历误差的途径: 第五章 GNSS测量的误差来 源 由于摄动力对卫 星轨道6个参数的影 响并不相同(见表 5.1.3),而且在对 卫星轨道摄动进行修 正时,所采用的各摄 动力模型精度也不一样,所以在以轨道改进法进行数据处理时, 根据引入轨道偏差改正数的不同,又分为短弧法和半短弧法
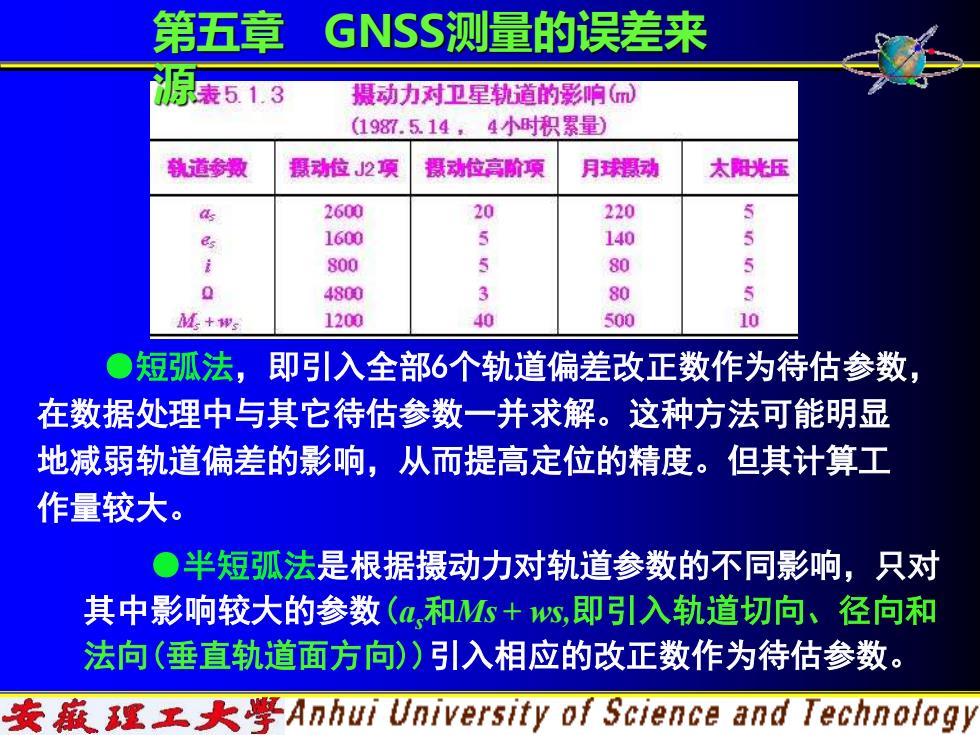
第五章 GNSS测量的误差来 表513 摄动力对卫星轨道的影响(m (198.5.14, 4小时积累量) 轨道参漫 摄动位J2项 摄动位高阶项 月球摄动 太阳光压 4 2600 20 220 ds 1600 5 140 5 800 5 80 4800 80 减+w 1200 40 500 10 ●短弧法,即引入全部6个轨道偏差改正数作为待估参数, 在数据处理中与其它待估参数一并求解。这种方法可能明显 地减弱轨道偏差的影响,从而提高定位的精度。但其计算工 作量较大。 。半短弧法是根据摄动力对轨道参数的不同影响,只对 其中影响较大的参数(a和M5+ws,即引入轨道切向、径向和 法向(垂直轨道面方向))引入相应的改正数作为待估参数。 安藏理工大学Anhui University of Science and Technology
●短弧法,即引入全部6个轨道偏差改正数作为待估参数, 在数据处理中与其它待估参数一并求解。这种方法可能明显 地减弱轨道偏差的影响,从而提高定位的精度。但其计算工 作量较大。 ●半短弧法是根据摄动力对轨道参数的不同影响,只对 其中影响较大的参数(as和Ms + ws,即引入轨道切向、径向和 法向(垂直轨道面方向))引入相应的改正数作为待估参数。 第五章 GNSS测量的误差来 源

第五章 GNSS测量的误差来 源 由表5.1.3可见,摄动力对轨道参数和M、+w的影响较大,也 就是说,对轨道的切向和径向影响较大。所以,当采用半短弧 法处理观测成果时,一般普遍引入轨道切向、径向和法向(垂直 轨道面方向)三个改正数作为待估量。半短弧法计算工作量较短 弧法明显减少,但同样可以有效地减弱轨道偏差的影响。根据 分析,目前经半短弧法修正后的卫星轨道误差将不会超过10。 轨道改进法一般用于精度要求较高的定位工作,需要测后处 理。 安徽理工大学导航定位技术应用研究所 余学祥 (0554)6633378 xxyu9166@aliyun.com NPTAI
由表5.1.3可见,摄动力对轨道参数as和Ms + ws的影响较大,也 就是说,对轨道的切向和径向影响较大。所以,当采用半短弧 法处理观测成果时,一般普遍引入轨道切向、径向和法向(垂直 轨道面方向)三个改正数作为待估量。半短弧法计算工作量较短 弧法明显减少,但同样可以有效地减弱轨道偏差的影响。根据 分析,目前经半短弧法修正后的卫星轨道误差将不会超过10m。 轨道改进法一般用于精度要求较高的定位工作,需要测后处 理。 第五章 GNSS测量的误差来 源

第五章 GNSS测量的误差来 源 ◆同步观测值求差。这一方法是利用在两个或多个观测站 上,对同一卫星的同步观测值求差,以减弱卫星轨道偏差的 影响。由于同一卫星的位置误差对不同观测站同步观测量的 影响具有系统性质,所以通过上述求差的方法,可以明显地 减弱卫星轨道误差的影响,尤其当基线较短时,其有效性甚 为明显。这种方法对于精密相对定位具有极其重要的意义。 ◆忽略轨道误差。这时简单地认为,由导航电文所获知的 卫星星历信息是不含误差的。很明显,这时卫星轨道实际存在 的误差将成为影响定价精度的主要因素之一。这一方法广泛地 应用于实时定位工作。 安徽理工大学导航定位技术应用研究所 145 余学祥0554)6633378xxyu9166@aliyun.com NPTAI
◆同步观测值求差。这一方法是利用在两个或多个观测站 上,对同一卫星的同步观测值求差,以减弱卫星轨道偏差的 影响。由于同一卫星的位置误差对不同观测站同步观测量的 影响具有系统性质,所以通过上述求差的方法,可以明显地 减弱卫星轨道误差的影响,尤其当基线较短时,其有效性甚 为明显。这种方法对于精密相对定位具有极其重要的意义。 第五章 GNSS测量的误差来 源 ◆忽略轨道误差。这时简单地认为,由导航电文所获知的 卫星星历信息是不含误差的。很明显,这时卫星轨道实际存在 的误差将成为影响定价精度的主要因素之一。这一方法广泛地 应用于实时定位工作

第五章 GNSS测量的误差来 5.1.2 隐星钟误差 由于卫星的位置是时间的函 数,因此GPS的观测量均以精密测 时为依据。在GPS测量中,无论是 码相位观测值还是载波相位观测 值,均要求卫星钟和接收机钟严 格同步。尽管GP$卫星均设有高精 度的原子钟,但它们与标准GPS时 之间仍存在着偏差或漂移。这些 偏差的总量约在1ms以内,由此引 起的等效距离误差可达300km。 安徽理工大学导航定位技术应用研究所 A1 余学祥(05546633378xxyu9166@aliyun.com NPTAI
由于卫星的位置是时间的函 数,因此GPS的观测量均以精密测 时为依据。在GPS测量中,无论是 码相位观测值还是载波相位观测 值,均要求卫星钟和接收机钟严 格同步。尽管GPS卫星均设有高精 度的原子钟,但它们与标准GPS时 之间仍存在着偏差或漂移。这些 偏差的总量约在1ms以内,由此引 起的等效距离误差可达300km。 5.1.2 卫星钟误差 第五章 GNSS测量的误差来 源