
◆时间响应及其组成 自由响应 强迫响应 )= 2sino,t+y(0)coso1-k1-元 cos@,t+ coS @t k1-2 零输入响应 零状态响应 控制的目的:强迫或希望系统按输入所指定规律输出 希望一:y(t)保留带o的强迫响应项 希望二:带。的自由响应项很快衰减到零 若做自由运动,系统回到平衡点 系统稳定性好 安徽科技学院机械工程学院
◆ 时间响应及其组成 ( ) ( ) ( ) 2 2 0 1 1 sin 0 cos cos cos 1 1 n n n n y F F y t t y t t t k k = + − + − − 零输入响应 零状态响应 自由响应 强迫响应 安徽科技学院机械工程学院 控制的目的:强迫或希望系统按输入所指定规律输出 希望一:y(t)保留带 的强迫响应项 希望二:带 的自由响应项很快衰减到零 若做自由运动,系统回到平衡点 系统稳定性好 n

◆时间响应及其组成 0=0no/+0)easo1-装1元osa+大1-Pos6W F.1 @ 现在来分析较为一般的情况,设系统的动力学方程为: a"()+a(t)+..+ay()+aor(t)=x(t) 欧拉公式:cosz= 2 ,snz e-e 2i 自由响应 强迫响应 方程解的般形式:r0=工Ae+∑4e+B间 零输入响应 零状态响应 式中,s,(i=1,2,…,n)为方程的特征根。安徽科技学院机械工程学院
◆ 时间响应及其组成 安徽科技学院机械工程学院 ( ) ( ) ( ) ( ) ( ) 1 1 1 0 cos ,sin 2 2 n n n n iz iz iz iz y t y t y t y t x t e e e e z z i − − − − + + + + = + − = = 现在来分析较为一般的情况,设系统的动力学方程为: a a a a 欧拉公式: ( ) ( ) ( ) 2 2 0 1 1 sin 0 cos cos cos 1 1 n n n n y F F y t t y t t t k k = + − + − − ( ) 1 2 ( ) 1 1 i i n n s t s t i i i i t A e A e B t = = 方程解的一般形式:y = + + 零输入响应 零状态响应 自由响应 强迫响应 式中,s i n i ( = 1, 2, , )为方程的特征根

◆时间响应及其组成 自由响应 强迫响应 方程解的般形式:y()=立4,e+∑4,e+B(④0 共轭特征根,S=α±j分别带入() 响应 iDDe (cosjsin Br) 2=D2ea-Br=D2e“(cos Bi--jsin Bt) 解的线性组合,也是微分方程的解。 y=e"(C,cos Bt-+C2 sin Bt)(积化和差) (指数函数发散或衰减; 正弦函数上下振荡)。 :决定自由响应是否衰减;B:决定自由响应振荡频率。 式中,s(i=1,2,,n)为方程的特征根。安徽科技学院机械工程学院
◆ 时间响应及其组成 安徽科技学院机械工程学院 ( ) 1 2 ( )( ) 1 1 1 i i n n s t s t i i i i t A e A e B t = = 方程解的一般形式:y = + + 自由响应 强迫响应 式中,s i n i ( = 1, 2, , )为方程的特征根。 共轭特征根,s j i = 分别带入(1) ( ) ( ) ( ) ( ) 1 1 1 2 2 2 cos sin cos sin j t t j t t y D e D e t j t y D e D e t j t + − = = + 响应 = = − ( )( ) 2 2 1 1 1 2 2 1 2 cos sin + sin tan t t C C C t C t C t C − + + 解的线性组合,也是微分方程的解。 y=e 积 y=e 化和差 (指数函数发散或衰减; 正弦函数上下振荡)。 :决定自由响应是否衰减; :决定自由响应振荡频率

◆时间响应及其组成 自由响应 强迫响应 方程解的一般形式:y()=∑A,e+∑4,e+B(0 sin+am名) 希望自由响应很快衰减→s实部为负→系统稳定。 讨论: ()阶次n和特征根s取决于系统固有特性,与初态无关; (2)拉氏变换所得输出是系统的零状态响应y()=L(G(s)·X(s): (3)对于线性定常系统:若x(t)引起的输出为y(),则x()引起的输出为y(t) 安徽科技学院机械工程学院
◆ 时间响应及其组成 安徽科技学院机械工程学院 ( ) 1 2 ( )( ) 1 1 1 i i n n s t s t i i i i t A e A e B t = = 方程解的一般形式:y = + + 自由响应 强迫响应 ( ) ( ) ( ) ( ( ) ( )) ( ) ( ) ( ) ( ) ( ) 1 ' ' 1 2 3 , i i s t L G s X s t s y t t y t − → → = 讨论: 阶次n和特征根 取决于系统固有特性,与初态无关; 拉氏变换所得输出是系统的零状态响应y ; 对于线性定常系统:若x 引起的输出 希望自由响应很快衰减 实部为负 系统 为 则x 引起的输出为 稳定。 。 2 2 1 1 1 2 2 + sin tan t C C C t C − + y=e
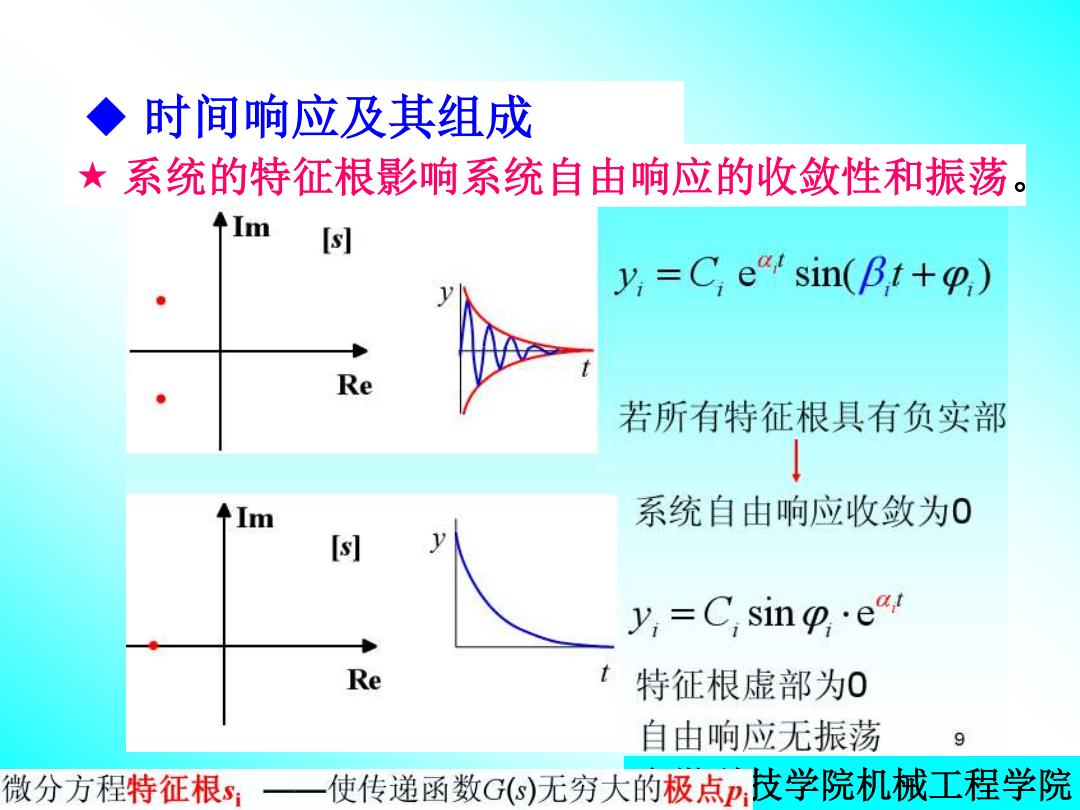
◆时间响应及其组成 ★系统的特征根影响系统自由响应的收敛性和振荡 Im y=C e sin(Bt+) Re 若所有特征根具有负实部 Im 系统自由响应收敛为0 y=C sin.ea Re 特征根虚部为0 自由响应无振荡 g 微分方程特征根s 使传递函数G)无穷大的极点,伎学院机械工程学院
◆ 时间响应及其组成 安徽科技学院机械工程学院 系统的特征根影响系统自由响应的收敛性和振荡