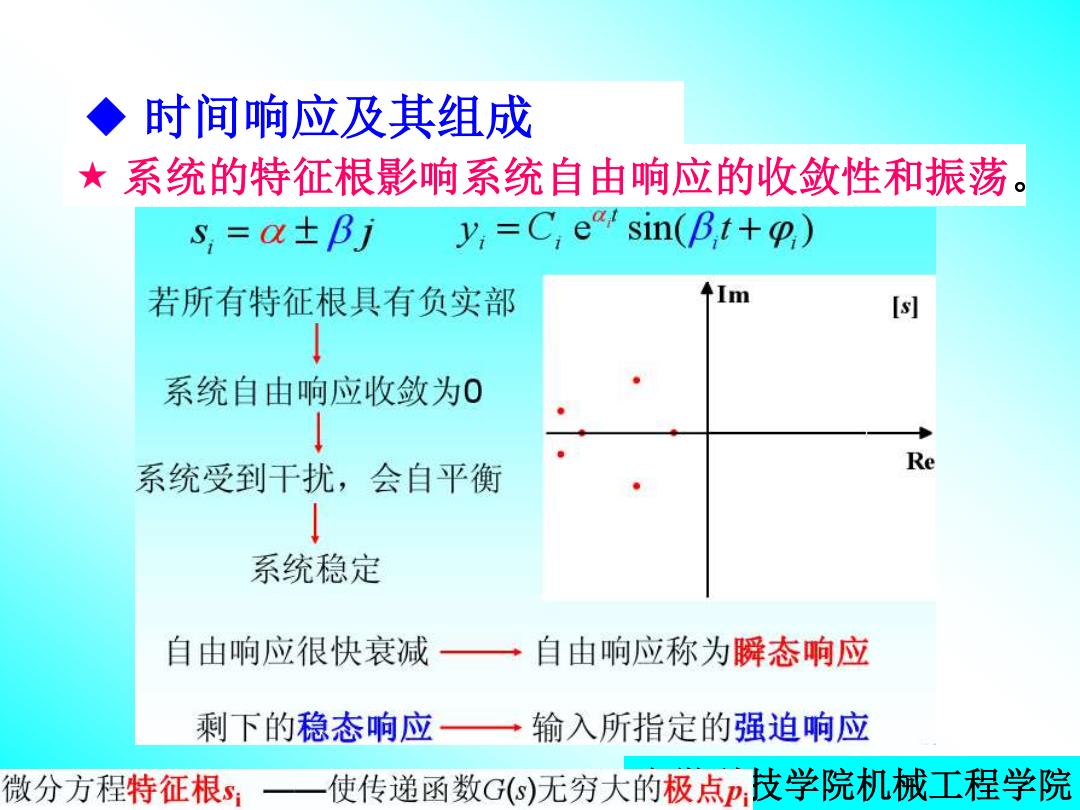
◆时间响应及其组成 ★系统的特征根影响系统自由响应的收敛性和振荡。 s=oa±βj y:=C,e sin(Bt+p) 若所有特征根具有负实部 m 系统自由响应收敛为0 系统受到干扰,会自平衡 Re 系统稳定 自由响应很快衰减一自由响应称为瞬态响应 剩下的稳态响应一 输入所指定的强迫响应 微分方程特征根✉ 使传递函数GS)无穷大的极点,技学院机械工程学院
◆ 时间响应及其组成 安徽科技学院机械工程学院 系统的特征根影响系统自由响应的收敛性和振荡
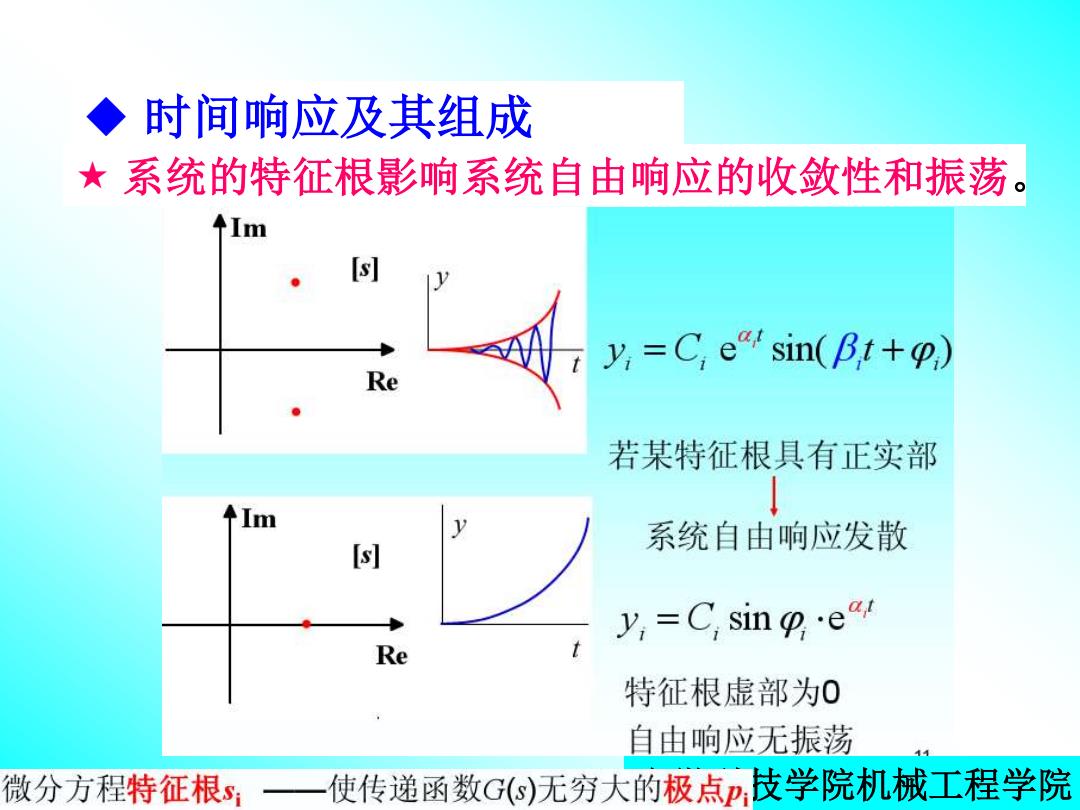
◆时间响应及其组成 ★系统的特征根影响系统自由响应的收敛性和振荡。 Im y,=C esin(Bt+p.) 若某特征根具有正实部 Im 系统自由响应发散 y,=C sin gea Re 特征根虚部为0 自由响应无振荡 微分方程特征根s: 使传递函数G)无穷大的极点p,技学院机械工程学院
◆ 时间响应及其组成 安徽科技学院机械工程学院 系统的特征根影响系统自由响应的收敛性和振荡

◆时间响应及其组成 ★系统的特征根影响系统自由响应的收敛性和振荡。 特征根的实部α越负 Im [s] 自由响应收敛越快 Re 特征根虚部β越大 s=a±Bj 自由响应振频越高 y =C,ea sin(B+) 若特征根虚部均为0一自由响应无振荡 仅剩指数函数ea×const一自由响应单调增加一发散 或单调减小一收敛 微分方程特征根s 使传递函数GS)无穷大的极点,技学院机械工程学院
◆ 时间响应及其组成 安徽科技学院机械工程学院 系统的特征根影响系统自由响应的收敛性和振荡
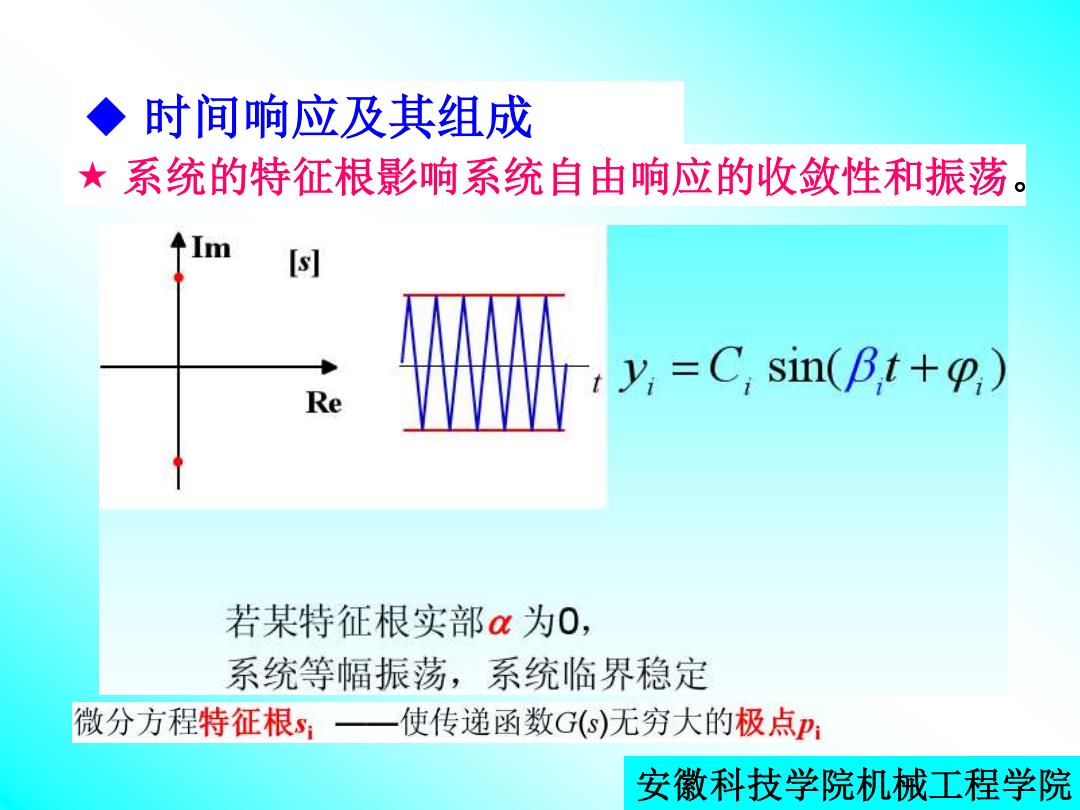
◆时间响应及其组成 ★系统的特征根影响系统自由响应的收敛性和振荡 [s] y =C.sin(Bt+) Re 若某特征根实部α为0, 系统等幅振荡,系统临界稳定 微分方程特征根s,一使传递函数G(s)无穷大的极点P: 安徽科技学院机械工程学院
◆ 时间响应及其组成 安徽科技学院机械工程学院 系统的特征根影响系统自由响应的收敛性和振荡
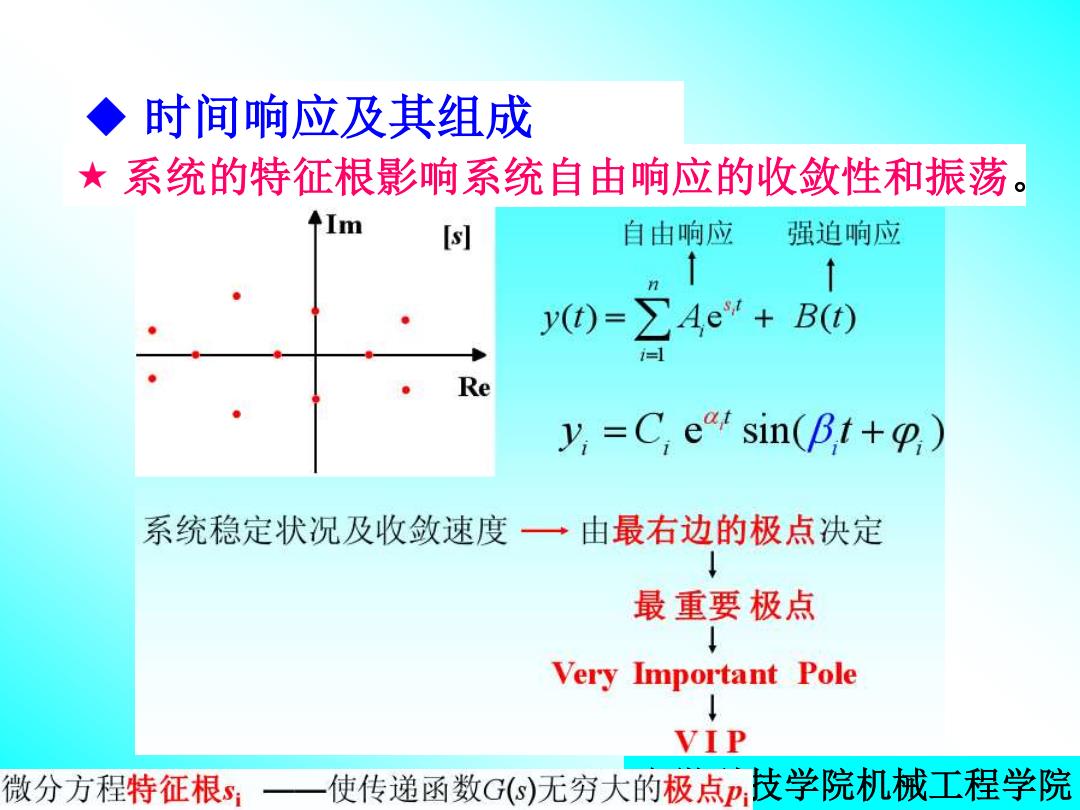
◆时间响应及其组成 ★系统的特征根影响系统自由响应的收敛性和振荡。 m 自由响应 强迫响应 y)=∑Ae+B0 Re y,=C eat sin(Bt+p) 系统稳定状况及收敛速度一由最右边的极点决定 最重要极点 Very Important Pole VIP 微分方程特征根s 使传递函数G)无穷大的极点,支学院机械工程学院
◆ 时间响应及其组成 安徽科技学院机械工程学院 系统的特征根影响系统自由响应的收敛性和振荡