
第二章系统的数学模型 要点:Laplacez变换及其逆变换;机械工程控制中如 何列写线性系统微分方程的问题以及列些时应注意之 点;传递函数的定义与概念,典型线性环节的传递函 数及其特性、传递函数的方框图与简化方法;系统的 状态空间模型及数学模型的MATLAB描述。 难点:传递函数的方框图与简化方法。 安徽科技学院机械工程学院
第二章 系统的数学模型 要点:Laplace变换及其逆变换;机械工程控制中如 何列写线性系统微分方程的问题以及列些时应注意之 点 ;传递函数的定义与概念,典型线性环节的传递函 数及其特性、传递函数的方框图与简化方法 ;系统的 状态空间模型及数学模型的MATLAB描述。 难点:传递函数的方框图与简化方法。 安徽科技学院机械工程学院

◆Laplacez变换 √Laplacez变换的定义及常用函数拉氏变换 √Laplace2变换的性质 √Laplace逆变换 √Laplace2变换的综合举例 安徽科技学院机械工程学院
◆ Laplace变换 安徽科技学院机械工程学院 ✓ Laplace变换的定义及常用函数拉氏变换 ✓ Laplace变换的性质 ✓ Laplace逆变换 ✓ Laplace变换的综合举例

√Laplace2变换的定义及常用函数拉氏变换 *Laplace2变换的定义:如果有一个以时间t为自变 量的实变函数f),它的定义域是≥0,那么)的 Laplace2变换定义为: F(s)=L f(t)=f(t)e"dr 注:s是复变量,s=o+jo(o,o均为实数),e“称为拉普拉 斯积分,F(s)是f(t)的拉普拉斯变换,它是一个复变函数,通 常也称F(s)为f(t)的象函数,而f(t)为F(s)的原函数,L表示进 行拉普拉斯变换的符号。 安徽科技学院机械工程学院
✓ Laplace变换的定义及常用函数拉氏变换 安徽科技学院机械工程学院 Laplace变换的定义:如果有一个以时间t为自变 量的实变函数f(t),它的定义域是t≥0,那么f(t)的 Laplace变换定义为: ( ) ( ) ( ) 0 st F s L f t f t e dt + − = = ( ) ( ) ( ) ( ) ( ) ( ) ( ) 0 , F F F L st e s f t s f t f t s + − 注: s是复变量,s= +j 均为实数 , 称为拉普拉 斯积分, 是 的拉普拉斯变换,它是一个复变函数,通 常也称 为 的象函数,而 为 的原函数, 表示进 行拉普拉斯变换的符号

√Laplace2变换的定义及常用函数拉氏变换 ★Laplace?变换的定义:如果有一个以时间t为自变 量的实变函数f(),它的定义域是≥0,那么f)的 Laplace2变换定义为: F(s)=L f(t)=f(t).e-"dt 说明:拉氏变换是这样一种变换,即在一定条件 下,它能把一实数域中的实变函数变换为一个在 复数域内与之等价的复变函数F(s)。 安徽科技学院机械工程学院
✓ Laplace变换的定义及常用函数拉氏变换 安徽科技学院机械工程学院 Laplace变换的定义:如果有一个以时间t为自变 量的实变函数f(t),它的定义域是t≥0,那么f(t)的 Laplace变换定义为: ( ) ( ) ( ) 0 st F s L f t f t e dt + − = = 说明:拉氏变换是这样一种变换,即在一定条件 下,它能把一实数域中的实变函数变换为一个在 复数域内与之等价的复变函数F(s)
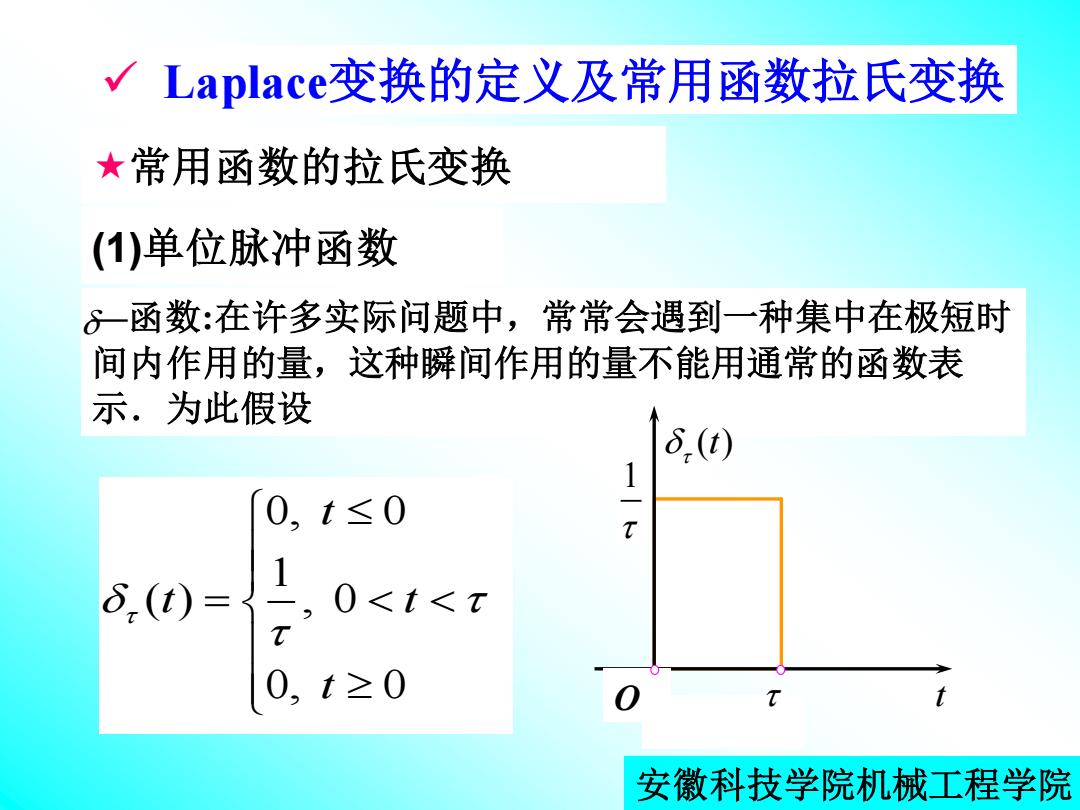
√Laplace?变换的定义及常用函数拉氏变换 ★常用函数的拉氏变换 (1)单位脉冲函数 ♂-函数:在许多实际问题中,常常会遇到一种集中在极短时 间内作用的量,这种瞬间作用的量不能用通常的函数表 示.为此假设 6,(t) 1 0,t≤0 1 δ,(t)= 0<t< 0,t≥0 安徽科技学院机械工程学院
安徽科技学院机械工程学院 ✓ Laplace变换的定义及常用函数拉氏变换 常用函数的拉氏变换 (1)单位脉冲函数 —函数:在许多实际问题中,常常会遇到一种集中在极短时 间内作用的量,这种瞬间作用的量不能用通常的函数表 示.为此假设 0, 0 1 ( ) , 0 0, 0 t t t t = O ( )t 1 t