
第6卷第4期 智能系统学报 Vol.6 No.4 2011年4月 CAAI Transactions on Intelligent Systems Ag2011 doi:10.3969/i.issn.1673-4785.2011.04.015 pH值系统变论域模糊控制器的设计及性能分析 佟世文 (中国天辰工程有限公司,北京100029)》 摘要:针对pH值非线性控制系统,设计了一种实时简化变论域模糊控制器.将变论域思想与实时模糊推理策略相 结合:一方面论域随着误差的减小而收缩,而论域的收缩相当于控制规则的增加,从而增加了控制精度;另一方面采 用实时模糊推理方法,即对于一个二入一出的模糊控制器,一次推理过程中最多只激活4条控制规则,在控制的过 程中只考虑这4条控制规则.这2种思想的结合使得控制规则的设计大大简化,可以采用批处理的方式设计控制器, 不仅加快了系统的动态响应,也提高了控制精度.仿真结果证实了这种控制方法的有效性. 关键词:pH系统;变论域;实时模糊推理;模糊控制器 中图分类号:TP273.4文献标识码:A文章编号:16734785(2011)04-036706 Design and performance analysis of a pH variable domain fuzzy control system TONG Shiwen China Tianchen Engineering Corporation,Beijing 100029,China) Abstract:The real-time simplified variable domain fuzzy control method for the control of a pH nonlinear system was proposed.The method combined the idea of variable domain with the real-time fuzzy inference strategy.On the one hand,the method increased the control accuracy by the contraction of the domain following the decrease of er- rors,which is equivalent to the increase of the control rules.On the other hand,the algorithm activated at most four control rules during each control cycle by using the real-time fuzzy reasoning method for a typical two-input one-output fuzzy controller.The consideration of the two ideas simplifies the design of the control rules,accelerates the dynamic response,and improves the control accuracy.The controller can be designed in a batch mode.The simulation results confirm that the method is effective. Keywords:pH system;variable domain;real-time fuzzy inference;fuzzy controller pH值酸碱中和过程是一个典型的非线性系统, 实时简化变论域模糊控制器6应用于pH值非线性 在工业上有着广泛的应用,如电厂、炼油厂的污水处 系统的控制中 理,集成电路的蚀刻,锅炉供水,制药厂的生化反应 1pH值系统建模 等.由于其本身的高度非线性,难以建立精确的线性 模型,使得多年来对这一被控对象的研究一直在进 如图1所示的是一个典型的pH值酸碱中和系 行.已有很多成果应用于pH值系统,有改进的PD 统CSTR反应器).设碱液的流量为U(t),浓度为 控制、神经网络控制2、模糊控制3]、变结构控 Calkali;酸液的流量为F(t),浓度为Cacid;酸碱中 制4、预测控制5)]等.这些方法中有的控制效果还 和后的混合液的流量为P(t).碱液与酸液在CSTR 有提高的余地,有的算法太复杂,不利于工业应用; 反应器中在搅拌器的作用下充分混合,发生中和反 有的算法的适应性较差,工艺条件的改变将导致模 应.通过调节碱液流量U(t),使混合后的出口液达 型误差增大,使控制效果变差.本文将变论域和实时 到要求的pH值.根据质量守恒及酸碱中和原理,可 模糊推理策略相结合,设计了一种既简单又好用的 得到如下模型: 收稿日期:2009-1201. 基金项目:国家自然科学基金资助项目(60774007) 通信作者:佟世文.E-mail:sun21st@sina.com

368· 智能系统学报 第6卷 F(t).C. U(f).C. 法,以pH值为被控变量,以碱液的流量U(t)作为 操作变量,以酸液的流量F(t)和混合液的流量P(t) 作为扰动变量.在整体上控制结构形式保持不变,但 AIC .001 在局部论域会随着误差的变化而伸缩,论域缩小相 当于控制规则的增加,在变论域机制下,可根据系统 的动态过程设计有限几个关键的控制规则,通过论 AT 001 域的收缩,在关键控制规则之间进行插值,相当于增 加了控制规侧,从而可以实现较精确的控制.这种控 P(t),pH 制算法很好地处理了“整体与局部”的关系,提高了 图1酸碱中和系统CSTR反应器 控制性能.另外采用了实时推理策略,即对于一个二 Fig.1 CSTR reactor of an acid-alkali neutralization system 入一出的模糊控制系统,每次最多只能激活4条控 制规则,在动态推理过程中,只需考虑这4条规则, h()s@=Ue(Caw-(t))- 而无需考虑所有的规则,从而可以采用实时动态推 dt 理的方式实现控制,控制算法简单,变论域配合实时 F(t)(Cacia +x(t)), 推理,在控制规则的设置上也可以大大简化,使这种 Adh()=U(t)+F(t)-P(t), 方法非常适合在线精确控制。 dt p(o=g*0+V+4 3模糊控制器设计 2K 采用典型的二入一出的控制结构 式中:h(t)为液位,m;C为碱液浓度,kmol/m3; (如图3所示),以给定pH值与实际pH值的误差e Ca为酸液浓度,kmol/m;x(t)为氢氧根离子和氢 及误差的变化c作为输入,以控制作用(碱液的流 离子浓度之差,kmol/m3;A为反应器的截面积,m2; 量U(t))作为输出.K。、K、Ku分别为误差e、误差 K。为水平衡常数, 的变化ec及增量的控制作用△u的调节因子.变量 2控制难点及控制策略 e、ee可以通过等式x=K。·e,y=K.e·ec标准化成 x、y.aα(x)B(y)、y(x,y)是标准化论域X、Y及Z上 根据所列方程,对模型进行仿真,可得在中性点 的伸缩因子,为了使系统在达到稳态时没有误差,需 pH=7附近的仿真曲线.从图2中可以看出pH值 要引用积分作用,因而采用增量算法。 是一个高度非线性的系统,对其进行控制主要有以 下难点, ax】 pH值pH x 模糊 系统 1)采用线性化模型进行控制器设计,在不同的 du/dr 推理 工作点时模型参数相差较大,难以准确描述被控过 程8],设计出的控制器控制效果不佳 1/2 2)采用其他的非线性方法,设计过程复杂2], 实时简化变论域模糊控制器 对系统的软硬件要求较高,不利于在实际中应用. 11 图3变论域模糊控制结构 10 Fig.3 Structure of the variable domain fuzzy control 9 8 7 设偏差e的语言变量为E,其相应的模糊子集 6 为A:(i=1,2,3,4,5),论域为X=[-2,2],模糊子 集的5个语言值为L(e)=(NB,NS,ZE,PS,PB),其 3 三角型隶属度函数如图4所示. 设偏差ec的语言变量为EC,其相应的模糊子集 t/min 为B0=1,2,3,4,5,6,7),论域为Y=[-2,2],模糊 图2pH值特性曲线 子集的7个语言值为L(ec)=(NB,NM,NS,ZE,PS, Fig.2 pH titration curve PM,PB),其三角型隶属度函数如图5所示 本文采用了一种实时简化变论域模糊控制算

第4期 佟世文:pH值系统变论域模糊控制器的设计及性能分析 ·369· 由于误差e、误差的变化ec是通过调节因子映 射到标准化论域X、Y上的,因此有x≤X,y≤Y再加 NB PS PB 1.0 上T1<1、T2<1、T3<1,可以得出a≤1B≤1、Y≤1. 论域会随着偏差的增大和减小而增大和减小,但不 -1 会超过标准论域.论域的收缩相当于控制规则的增 0 -2.0-1.33-0.66 0 0.66 1.33 2.0 加,从而既保证了初始论域的设置又提高了控制精 图4变量e的隶属度函数 度.在这种情况下,专家的经验,区域的划分以及隶 Fig.4 Membership function of variable e 属度函数的选择都变得不重要了,只要掌握规则的 EC 大致趋势就可以了,因而可以采用较少的控制规则 NB NMNS ZE PS PMPB 实现较精确的控制[91o 3.2实时推理策略 由典型的二阶系统动态响应曲线,根据偏差和偏 0-2.0-1.5-1.0-0.500.51.01.5 20 差的变化便可决定相应的控制作用大小,在波峰和波 谷处,误差的变化C为零,如果输出值远小于给定 图5变量ec的隶属度函数 Fig.5 Membership function of variable ec 值,即E=PB,这时要使误差减小,需要增大控制作 设输出控制量△u的语言变量为△U,其相应的模 用,可将控制作用输出设置成PB.如果输出值远大于 糊子集为Cnm(m=1,2,3,4,5,6,7),论域为Z,划分成7 给定值,即E=NB,这时要使误差减小,需要减小控制 个等级Z={-3,-2,-1,0,+1,+2,+3},模糊子集 作用,可将控制作用输出设置成NB.在曲线误差等于 Cn的7个语言取值为L(△u)=(NB,NM,NS,ZE,PS, 零的附近,控制作用的可采用和误差的变化EC相同 PM,PB),相应的隶属度如表1所示 的.这样,控制规则的设计就变得非常简单,只需分别 表1变量△u随等级变化的隶属度函数 考虑误差E为零及误差的变化EC为零的点.因而可 Table 1 Membership function of variable Au 以得到如表2所示的简化控制规则. 表2控制规则表 等级 4.(2) -3-2-10+1+2+3 Table 2 Map of the control rules NB1.00.70.30000 E △U NM0.71.00.70.3000 NB NS ZE PS PB Ns0.30.71.00.70.3 0 0 NB NB AUZE00.30.71.00.70.30 NM ZE NM ZE Ps000.30.71.00.70.3 NS NS EC ZE NB NS PB PM0000.30.71.0 0.7 ZE PS PB00000.30.71.0 PS PS PM ZE PM ZE PB PB 3.1变论域策略 变论域是通过伸缩因子aα(x)、B(y)、y(x,y)与 由三角型的隶属度函数可以看出,任何输入最 标准化论域X、Y、Z相乘作为新的论域来实现的.伸 多属于2个隶属度函数,因此,对于一个双输人系 缩因子有多种定义方法,本文采用如下的指数型伸 统,一次最多只能激活4条控制规则21.具体来 缩因子 说,假设在某一时刻k,(x,y)是标准化的输入变量, 属于x的隶属度函数为4,和41,属于y的隶属度 B()=['],0<<1, 函数为g,和g+·这样,就可以激活L、L+、 1》、1+少4条控制规则.相应地就可获得4 (x,)=[][]]°,0<,<1. 条“f-hen”规则: If(=L()U(y=L(),then(Au =Li); 式中:y(x,y)是标准化的论域Z的伸缩因子,用于 If(L()U(y=LD),then(Au=L); 调节输出论域的大小,当输入论域随着误差的减小 If())U(y=L),then(Au=L) 而收缩时,输出论域也应该随之减小,以便使调节过 I(=)U(y=L)),then(Au =L). 程更加精细。 查询4u的隶属度函数表可以获得4个1×7的隶属
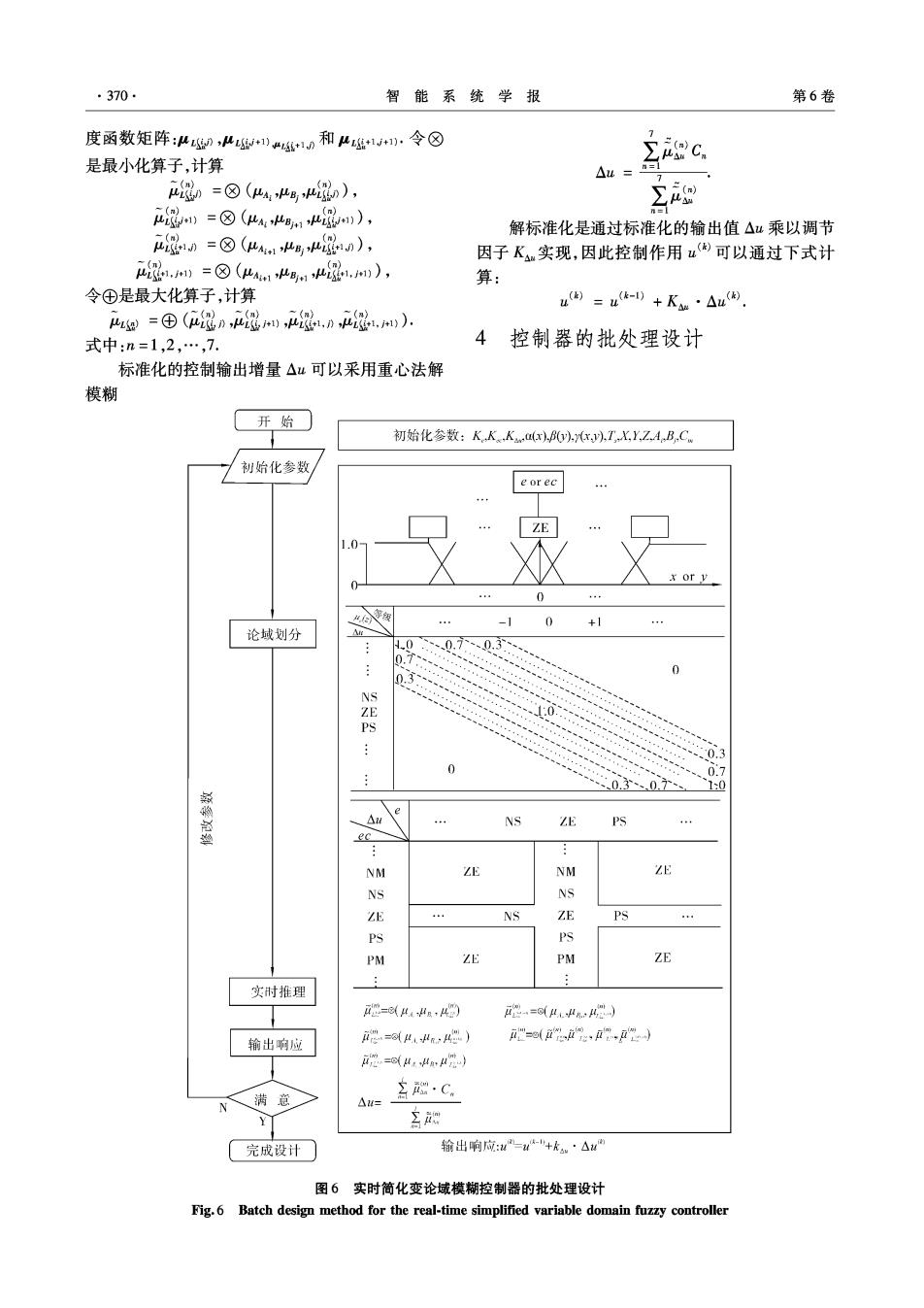
370 智能系统学报 第6卷 度函数矩阵:u,1和1,令⑧ 7 是最小化算子,计算 C. △u= 8=⑧(4g,⑧), 8)=⑧(,hg1h8n), 解标准化是通过标准化的输出值△w乘以调节 品0=⑧(4hh), 因子K实现,因此控制作用u可以通过下式计 绿.)=⑧(1hgh8绿m), 算: 令④是最大化算子,计算 u因=uk-》+K·△u因. ue=①(8nn,,n是w). 式中:n=1,2,…,7. 4 控制器的批处理设计 标准化的控制输出增量△u可以采用重心法解 模糊 开始 初始化参数:K,K,(x)fy)x),T,X,Y,Z.A.B.C 初始化参数 e orec ZE x or v 0 +1 论域划分 0 0,7、0.3 0.7 0 0.3 10. S 0.3 0 0.7 0.3、0.7 10 △ NS ZE PS ec NM ZE NM ZE NS NS ZE 44 NS ZE PS PS PS PM ZE PM ZE 实时推理 =(以4g,4 迟=(4L44) 输出响应 0=4r>4) =@(ii9,a,) i2=6(44) 、满意 名C △u= Y 名 完成设计 输出响应:=-"+ka·△ 图6 实时简化变论域模糊控制器的批处理设计 Fig.6 Batch design method for the real-time simplified variable domain fuzzy controller
第4期 佟世文:pH值系统变论域模糊控制器的设计及性能分析 ·371· 变论域配合实时推理,再加上控制规则的设计 模糊控制方法较其他2种方法能更快地进入稳态过 是根据典型的二阶动态响应过程,具有形式不变性, 程且没有偏差.其他2种方法的动态响应较慢,控制 使得控制器的设计变得非常简单、通用,可以采用批 效果不太理想, 处理的方式进行设计(如图6所示).只需事先设计 好伸缩因子a(x)B(y)、y(x,y),调节因子K。、K K,输人论域X、Y,输出论域Z,及其模糊子集划分 A:、B、Cm,按着图6的流程便可生成一个实时简化 变论域模糊控制器,再根据输出的动态响应曲线适 04 当调节这些初始化参数,直到获得满意的结果.换成 其他的被控过程,无需再进行具体的论域划分、控制 规则设计以及推理设计,只要初始化参数,执行批处 3.1 理程序便可完成控制器的设计. 5仿真及性能分析 实时简化变论域模糊控制 为验证控制器的性能,在Matlab的Simulink环 -----…模糊控制 境下建立pH值系统的C-S函数模型,设F=0.112 --PID控制 m/min,P =0.224 m/min,C.id =0.001 kmol/m3, Ca=0.001(kmo/m3,A=2m2,K=10-4,初始液 位h=4m.pH的设定值分别取6.5、7.0和7.5,实 时简化变论域模糊控制器的参数K。=0.0248, K=0.0018,Ka=0.3,a=0.1,B=0.1,Y=0.01, 图83种控制方法的相平面分析 采样时间0.38;普通模糊控制器的参数与实时简化 Fig.8 Phase plane analysis of three control methods 变论域模糊控制器的参数相同,只是论域不随误差 6 结束语 的变化而变化;PD控制器的参数为P=0.12,1=0. 2,K,=0,进行仿真比较研究,图7是3种控制方法 本文建立了酸碱中和pH值控制系统的数学模 型,分析了控制难点,设计了一种实时简化变论域的 的仿真比较,上部分是pH值输出,下部分是控制器 输出,即碱液的流量。 模糊控制算法并进行了仿真研究.通过和普通模糊 7.5 控制方法及PD控制方法相比较,证实本文的方法 7.0 6.5 简单、实用、控制效果好,非常适合对实时性和精确 性要求都比较高的场合.变论域配合实时推理,再加 6.0 0 4 上控制规则的形式不变性,使得这种方法可采用批 t/min 0.3 处理的方式进行控制器设计,也可以应用于其他的 0.2 单入单出的非线性系统的控制中.针对本文的内容 还可以开展后续的研究工作.主要有以下2个方面: 1)研究控制规则的减少对稳定性的影响;2)研究控 3 4 t/min 制参数的最优设计 图73种控制方法的仿真结果 参考文献: Fig.7 Simulation results of three control methods 从图7中可以看出,采用实时简化变论域模糊 [1]赵彦华,麻红昭.一种用于pH值控制的非线性系统的 控制算法,不仅动态响应大大变快,从PD控制的分 实现[J].工业仪表与自动化装置,2004,3:4043. 钟级提高到秒级,而且稳态精度也大幅提高.而且这 ZHAO Yanhua,MA Hongzhao.A new nonlinear system de- 种算法的计算量很小,非常适合实时在线应用.为了 signed for use with pH control[J].Industrial Instrumenta 对3种控制方法进行更清晰的比较,针对pH=7.0 tion Automation,2004,3:40-43. 的控制曲线,分别对3种方法的e和ec作相平面分 [2]HADJISKI M,BOSHNAKOV K,GALIBORA M.Neural 析(如图8所示),从图中可以看出实时简化变论域 networks based control of pH neutralization plant C]// 2002 First International IEEE Symposium on Intelligent Sys-