
第6卷第5期 智能系统学报 Vol.6 No.5 2011年10月 CAAI Transactions on Intelligent Systems 0ct.2011 doi:10.3969/i.i8sn.1673-4785.2011.05.006 RBF神经网络的行车路径代价函数建模 陈亮,何为,韩力群 (北京工商大学计算机与信息工程学院,北京100048) 摘要:行车路线优化是城市智能交通系统的研究热点之一,对整个交通系统的优化起着重要作用.分析了影响行 车时间的各种因素,结合图论中最短路径算法,建立了基于RBF神经网络的路径代价函数模型.基于该函数模型,可 以计算出交通图中任意给定两地间的时间最优路径.将该模型应用于实际路况进行有效性验证,得到了有实用价值 的结果,说明了该模型的正确性和有效性. 关键词:智能交通;路径代价函数;行车路线优化;RBF神经网络;图论 中图分类号:TP391.4文献标志码:A文章编号:16734785(2011)050424-08 Radial basis function neural network modeling of the traffic path cost function CHEN Liang,HE Wei,HAN Liqun (College of Computer and Information Engineering,Beijing Commercial and Industrial University,Beijing 100048,China) Abstract:Vehicle route optimization is one of the hot topics in research on urban intelligent transportation systems (ITS),and it plays an important role in the optimization of the entire transportation system.This paper analyzed various factors that affect the travel time and established a path cost function model with an radial basis function neural network,based on the shortest paths algorithms in graph theory.By this function model,the time-oriented optimal path between any two given places on a traffic map can be calculated.The model was applied to actual traf- fic to validate the effectiveness,and its results are of practical value,showing the correctness and validity of the model. Keywords:intelligent transportation;path cost function;vehicle route optimization;radial basis function neural network;graph theory 在城市智能交通系统中,行车路线优化对整个 约束解决最短路径问题4 交通系统的优化起着重要作用,选取最优车辆行车 道路交通网络的实际情况非常复杂,每个路段 路线,可以加快车流速度,减少拥堵发生,还能减少 的行车时间除了与距离有关外,还与路宽、路况、气 因为堵车而造成的交通车辆刮蹭等事故的概率,因 候及行车时段等诸多因素相关,因此最短路径并不 此,该课题的研究具有重要的实用意义. 意味着最短行车时间,不能简单地用路径长度计算 行车路线优化属于路径优化问题.目前关于路径 路径的代价值51.鉴于此,本文从实际情况出发,综 优化的研究主要集中在如何找到最短路径,其中常见 合考虑了各种影响行车时间的主要因素,建立了较 的一类方法是采用图论中的D以sta算法,具体实现算 为实用的路段代价函数模型并进行了实验验证. 法有A--star、Bellman、Ford2 Moore、Foyd等2];另一类 常用方法是基于蚁群算法的解决方法,如2007年 1路径代价函数及其影响因素分析 Horoba等人提出的基于随机过程的改进蚁群算法最短 图论中每个弧段都可用其代价函数值表示,2 路径寻优3],2009年Punyaslok提出的多网络流最优化 个给定点之间的路径代价函数值则可用构成该路径 框架,2010年Zakzouk提出的基于蚁群算法利用模糊 的所有弧段的代价函数值之和表示.2个给定点间 收稿日期:20110422. 的最优路径即指所有可达路线中代价函数值最小的 通信作者:陈亮.E-mail:newboy_01@163.com 路径6

第5期 陈亮,等:RBF神经网络的行车路径代价函数建模 ·425· 实际应用中,弧段对应于两相邻路口之间的路 种影响因素的完全搭配可产生243个样本对,而每 段,路径对应于出发地到目的地之间的行车路线,代 个样本对中的教师信号必须来自与输入条件相符的 价函数值则对应于行车时间代价.实际道路中,很多 实际情况.为了减少工作量,采用正交实验设计法来 因素都会影响车辆通过路段的时间,表1列出了可 构造样本集,其优点是:正交表能在保证采集数据均 能影响车辆通过路段时间的主要因素[们 匀分布的前提下,大大减少训练网络所需的样本数 表1车辆通行时间的影响因素 本文将每个影响因素分成3个水平,如表2所示.表 Table 1 The influencing factors of vehicle travel time 2给出了水平因素表,1~是对道路通行时间不 影响因素 同的影响因素,再将每一个影响因素具有的3个水 时间段、天气情况(风、雨、雪、雾、沙尘)、季 平填入表中. 自然 节变化: 表2正交实验法水平因素表 Table 2 The level of factor orthogonal experiment table 车道数、车辆转向、自助红绿灯数量、路段长 系统 度、实时交通路况 因 素 水平 第2 名3 多 xs 管理 交通事故、交通管制、交通限行 水平1畅通1~20 ,≤500 直行 在诸影响因素中,可进一步筛选出相互独立的 水平2缓行31 500<,≤1000左转 主要因素.经过深人调研,本文确定了5个相互独立 水平3拥堵42 x4>1000 右转 的影响因素:实时交通路况、车道数(路宽)、道路长 采用的正交试验如表3所示.将5个不同因素 度、自助红绿灯数量以及车辆转向 的不同水平分别排列组合得到的18种实验组合情 2基于RBF网络的路段代价函数建模 况.虽然只给出了18种实验组合情况,但是用这个 表设计的训练集保证了实验数据的代表性, 在实际道路中,车辆通过路段的时间与其影响 表3正交实验设计表 因素之间存在着严重的非线性和不确定性,因此很 Table 3 Orthogonal experiment 难用解析式来表达.人工神经网络适于处理非线性 样本号 竹 节 ¥4 问题,利用神经网络建立路径代价函数模型,是一种 0 0 0 0 0 可行的途径⑧].适合拟合非线性关系的神经网络主 0 2 1 要有BP网络和RBF网络,经实验对比,采用效果较 0 2 2 好的RBF网络进行建模91」 4 1 0 0 1 1 2.1基于正交实验的训练集设计 5 1 1 2 2 6 2 0 0 RBF网络的输入是影响车辆通行时间的因素, 2 教师信号是车辆通过路段的实际时间.本文所确定 P 0 的影响因素包括:实时路况x1、车道数量2、行人自 9 0 2 1 助式红绿灯数量x3、路段长度x4、车辆在路口的转 10 2 1 向方式5 11 0 2 可以看出,上述影响因素既有语言变量,又有数 12 0 值变量.首先,对各影响因素进行数值化和离散化 13 0 1 2 0 其中:x1为语言变量,根据北京市交通管理局现有 14 1 0 1 标准划分,共分为3种路况:“畅通”、“缓行”、“拥 15 1 0 2 堵”,与3个语言值对应,x1取值分别为0、1、2;x2可 16 2 0 1 2 直接采用实际车道数,分为1~2条、3条、4条3种 公 2 1 0 2 0 情况,2取值分别对应为0、1、2;行人自助式红绿灯 e 2 0 1 数量x3,可直接采用实际数量,取值分别为0、1、2. 2.2基于RBF网络的路段代价函数建模 路段长度4可离散为3个区间,分别为小于500m、 由于采集到的输入输出数据取值范围差别很 500~1000m、大于1000m,对应的x4取值为0、1、 大,需进行归一化处理,将输入数据归一化到[-1, 2;x也是语言变量,可分为“直行”、“左转、“右转” 1]区间,教师信号的时间单位采用小时,归一化到 3种情况01,分别用0、1、2表示.按照上述规定,5 (0,1]区间四.数据归一化后的情况如表4所示
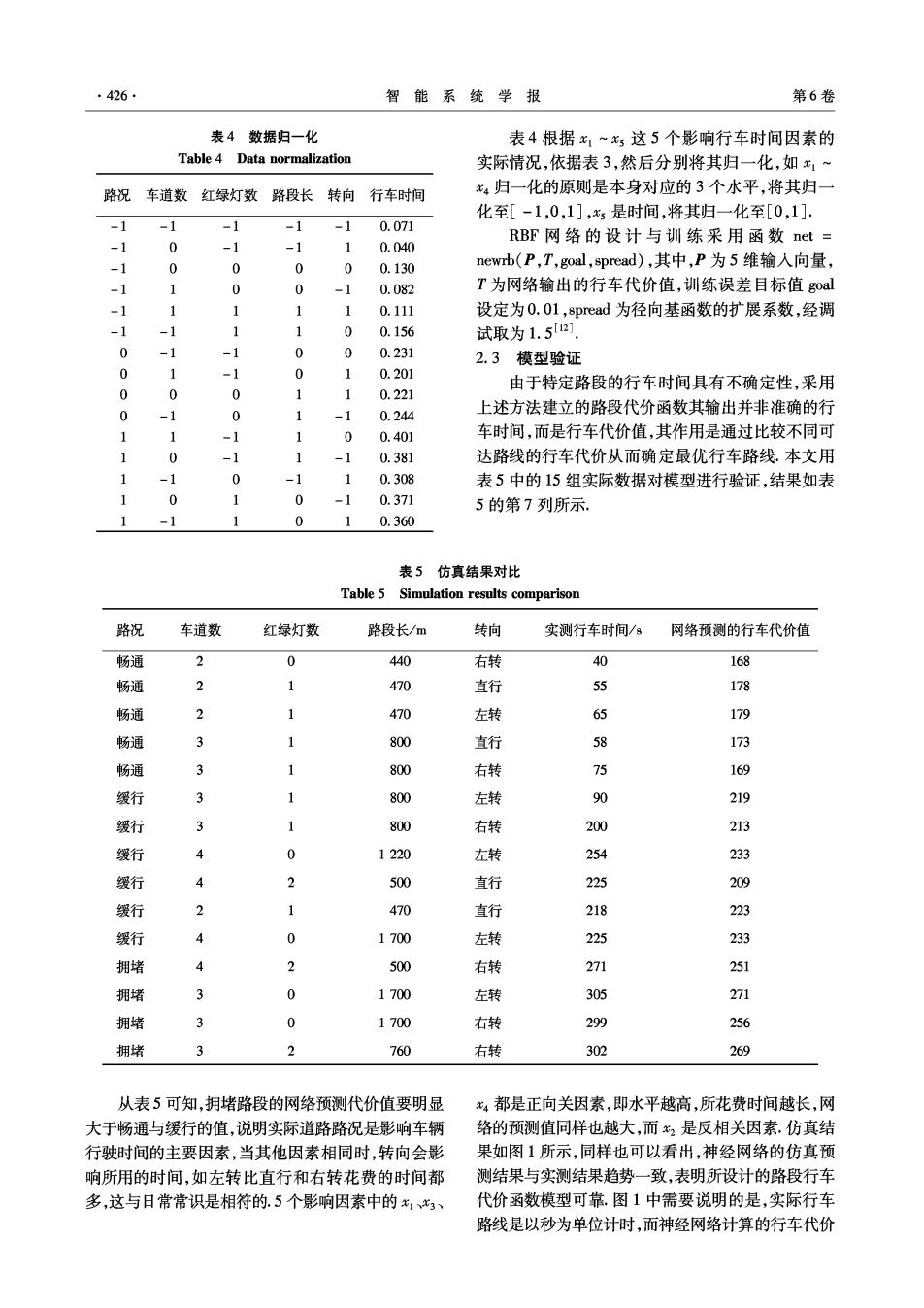
·426 智能系统学报 第6卷 表4数据归一化 表4根据x1~x这5个影响行车时间因素的 Table 4 Data normalization 实际情况,依据表3,然后分别将其归一化,如x1~ 路况车道数 红绿灯数路段长转向 行车时间 4归一化的原则是本身对应的3个水平,将其归一 化至[-1,0,1],是时间,将其归一化至[0,1]. -1 -1 -1 -1 -1 0.071 0 RBF网络的设计与训练采用函数net= -1 -1 -1 0.040 -1 0 0 0 0 0.130 newb(P,T,goal,spread),其中,P为5维输人向量, -1 0 0 -1 0.082 T为网络输出的行车代价值,训练误差目标值goal -1 1 1 0.111 设定为0.O1,spread为径向基函数的扩展系数,经调 -1 1 1 0 0.156 试取为1.52 0 -1 -1 0 0 0.231 2.3模型验证 0 1 -1 0 1 0.201 由于特定路段的行车时间具有不确定性,采用 0 1 0.221 0 -1 0 -1 0.244 上述方法建立的路段代价函数其输出并非准确的行 1 -1 0 0.401 车时间,而是行车代价值,其作用是通过比较不同可 -1 1 -1 0.381 达路线的行车代价从而确定最优行车路线.本文用 0 0.308 表5中的15组实际数据对模型进行验证,结果如表 1 0 0 0.371 5的第7列所示 0.360 表5仿真结果对比 Table 5 Simulation results comparison 路况 车道数 红绿灯数 路段长/m 转向 实测行车时间/8 网络预测的行车代价值 畅通 2 0 440 右转 168 畅通 2 1 470 直行 55 178 畅通 2 1 470 左转 65 179 畅通 3 800 直行 58 173 畅通 800 右转 75 169 缓行 3 800 左转 90 219 缓行 3 1 800 右转 200 213 缓行 4 0 1220 左转 254 233 缓行 2 500 直行 225 209 缓行 470 直行 218 223 缓行 0 1700 左转 225 233 拥堵 2 500 右转 271 251 拥堵 3 0 1700 左转 305 271 拥堵 0 1700 右转 299 256 拥堵 3 2 760 右转 302 269 从表5可知,拥堵路段的网络预测代价值要明显 x4都是正向关因素,即水平越高,所花费时间越长,网 大于畅通与缓行的值,说明实际道路路况是影响车辆 络的预测值同样也越大,而2是反相关因素.仿真结 行驶时间的主要因素,当其他因素相同时,转向会影 果如图1所示,同样也可以看出,神经网络的仿真预 响所用的时间,如左转比直行和右转花费的时间都 测结果与实测结果趋势一致,表明所设计的路段行车 多,这与日常常识是相符的.5个影响因素中的x1x3、 代价函数模型可靠.图1中需要说明的是,实际行车 路线是以秒为单位计时,而神经网络计算的行车代价
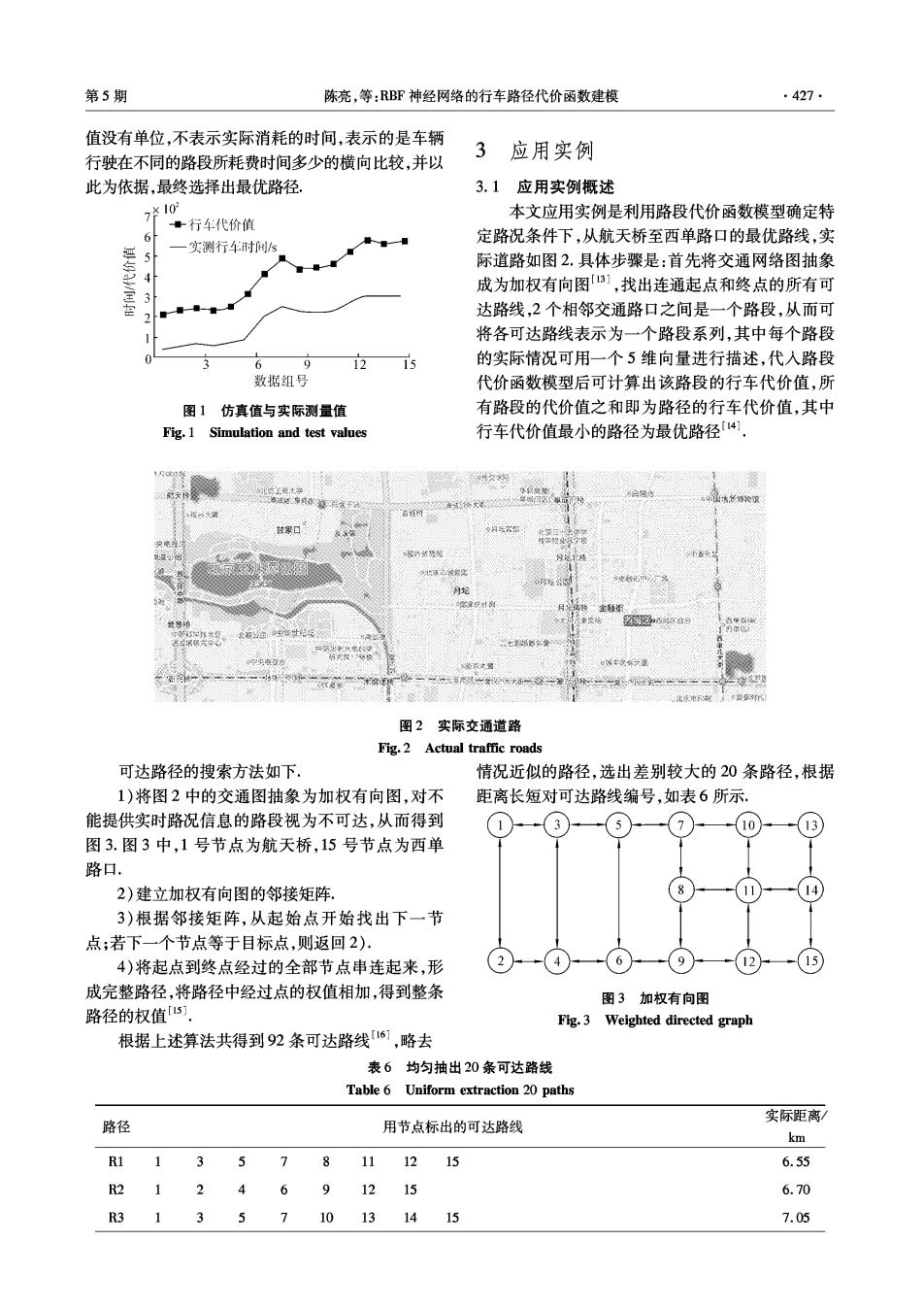
第5期 陈亮,等:RBF神经网络的行车路径代价函数建模 .427… 值没有单位,不表示实际消耗的时间,表示的是车辆 3应用实例 行驶在不同的路段所耗费时间多少的横向比较,并以 此为依据,最终选择出最优路径 3.1应用实例概述 7*10 本文应用实例是利用路段代价函数模型确定特 ·行车代价值 6 定路况条件下,从航天桥至西单路口的最优路线,实 -实测行车时问s 际道路如图2.具体步骤是:首先将交通网络图抽象 成为加权有向图3],找出连通起点和终点的所有可 3 达路线,2个相邻交通路口之间是一个路段,从而可 将各可达路线表示为一个路段系列,其中每个路段 6 9 12 的实际情况可用一个5维向量进行描述,代入路段 数据组号 代价函数模型后可计算出该路段的行车代价值,所 图1仿真值与实际测量值 有路段的代价值之和即为路径的行车代价值,其中 Fig.1 Simulation and test values 行车代价值最小的路径为最优路径4」 创 月坛 图2实际交通道路 Fig.2 Actual traffic roads 可达路径的搜索方法如下, 情况近似的路径,选出差别较大的20条路径,根据 1)将图2中的交通图抽象为加权有向图,对不 距离长短对可达路线编号,如表6所示. 能提供实时路况信息的路段视为不可达,从而得到 10 13 图3.图3中,1号节点为航天桥,15号节点为西单 路口. 2)建立加权有向图的邻接矩阵 14 3)根据邻接矩阵,从起始点开始找出下一节 点;若下一个节点等于目标点,则返回2). 4)将起点到终点经过的全部节点串连起来,形 2 6 9 12 15 成完整路径,将路径中经过点的权值相加,得到整条 图3加权有向图 路径的权值5] Fig.3 Weighted directed graph 根据上述算法共得到92条可达路线16,略去 表6均匀抽出20条可达路线 Table 6 Uniform extraction 20 paths 实际距离 路径 用节点标出的可达路线 km R1 13 5 7 1215 6.55 R2 1246 9 12 15 6.70 R3 135710 131415 7.05
·428. 智能系统学报 第6卷 续表6 实际距离/ 路径 用节点标出的可达路线 km R4 1 12 15 7.60 R5 6 9 11 14 15 8.05 6 1 6 9 14 15 8.20 R7 3 5 8 11 10 13 14 15 8.55 R8 1 2 3 1 8 11 12 夕 9.05 R9 1 8 9.15 R10 10 13 小 10.10 RI1 10 14 15 10.55 2 15 11.00 12 15 11.60 R14 10 13 14 11 12 15 11.95 1 1 10 13 14 15 12.45 R16 14 15 13.05 R17 4 6 5 8 9 2 11 10 6 14 15 13.50 R18 1 3 4 6 5 7 10 13 14 8 9 12 15 14.00 R19 3 4 6 > 9 2 11 10 13 14 14.40 R20 3 6 7 10 6 12 15 14.45 表6为所有可达路径中均匀抽取出的20条可 交通图,其中细线路段为畅通,粗线路段为缓行,粗 达路径,按实际距离从小到大排序,可知,最短可达 虚线路段为拥堵。 路线的距离为6.55km,最长可达路线的距离为 结合图4中实际的交通路况,并利用路段行车 14.45km. 代价函数模型计算表6中各可达路线的行车代价 3.2确定最优行车路线 值,将得到的行车代价值从小到大排序,结果如表7 图4给出了早上7:00时上述路段的实时路况 所示 西城区 序黑吸行 图4实时交通路况 Fig.4 Real time traffic