
第6卷第2期 智能系统学报 Vol.6 No.2 2011年4月 CAAI Transactions on Intelligent Systems Apr.2011 doi:10.3969/j.is3n.16734785.2011.02.007 一种带禁忌搜索的粒子并行 子群最小约简算法 马胜蓝,叶东毅 (福州大学数学与计算机科学学院,福建福州350108) 摘要:为了提高基于群体智能的粗糙集最小属性约简算法的求解质量和计算效率,提出一个结合长期记忆禁忌搜 索方法的粒子群并行子群优化算法.并行的各子群不仅具有禁忌约束,而且包含多样性和增强性策略.由于并行的 子群共同陷入局部最优的概率小于一个粒子群陷入局部最优的概率,该算法可提高获得全局最优的可能性,并诚少 受初始粒子群体的影响.多个UCI数据集的实验计算表明,提出的算法相对于其他的属性约简算法具有更高的概率 搜索到最小粗糙集约简.因此所提出的算法用于求解最小属性约简问题是可行和较为有效的, 关键词:属性约简;粗糙集;禁忌搜索:粒子群优化算法;并行子群 中图分类号:TP18文献标识码:A文章编号:16734785(2011)02-013209 A minimum reduction algorithm based on parallel particle sub-swarm optimization with tabu search capability MA Shenglan,YE Dongyi (College of Mathematics and Computer Science,Fuzhou University,Fuzhou 350108,China) Abstract:In order to improve the solution quality and computing efficiency of rough set minimum attribute reduction algorithms based on swarm intelligence,a parallel particle sub-swarm optimization algorithm with long-memory Tabu search capability was proposed.In addition to the taboo restriction,some diversification and intensification schemes were employed.Since parallel sub-swarms have a lower probability of simultaneously getting trapped in a local opti- mum than a single particle swarm,the proposed algorithm enhances the probability of finding a global optimum and decreases the influence of initial particles.Experimental results on a number of UCI datasets show that the proposed algorithm has a higher probability of finding a minimum attribute reduction in rough sets compared with some exist- ing swarm intelligence based attribute reduction algorithms.Therefore,the proposed algorithm is feasible and rela- tively effective for the minimum attribute reduction problem. Keywords:attribute reduction;rough set;tabu search;particle swarm optimization;parallel particle sub-swarm 作为特征选择的一个有效方法「12],粗糙集属Hdar等人提出将禁忌算法用于最小约简的搜 性约简及其算法近年来得到了广泛的研究34].其 索;而文献[8]和[9]则探讨了粒子群方法在求解 中,对于NP难的最小属性约简问题3)的研究也取 最小约简问题中的应用.相对启发式属性约简算法 得了新的进展,提出了若干基于进化计算或群体智 而言,这些最小约简算法提高了求得最小约简的可 能的最小约简算法.例如,Wroblewski和Bazan等利 能性,但是在求解质量和计算效率方面仍有待进一 用遗传算法寻找最小约简[S);R.Jensen等提出的基 步改进。 于蚁群算法的最小约简算法6;最近,Abdel-Rahman 针对上述情况,提出了一个带长期记忆的禁忌 搜索和并行子群粒子群优化方法相结合的最小属性 收稿日期:2010-0307. 约简算法.PS0算法简单、易于实现,通常比遗传算 基金项目:国家自然科学基金资助项目(60805042):福建省自然科学 基金资助项目(2010J01329). 法收敛速度快;另一方面,应用蚁群算法求解最小属 通信作者:叶东毅.E-mai:yiey@fzu.eu.cn. 性约简问题(如AntRSAR[6])需要采取和属性个数

第2期 马胜蓝,等:一种带禁忌搜索的粒子并行子群最小约简算法 ·133· 一致的种群规模,当规模较大时,计算复杂度明显 指包含属性个数最少的一个属性约简, 增加.而应用PS0算法则没有这方面的限制.本文 所有属性约简的交集为核,记为 中并行的各子群不仅具有禁忌约束,而且包含多样 Core(C)=n Red. 性和增强性策略,采用这2种策略主要是为了降低 1.2禁忌搜索 算法陷入局部极小的可能性.实验计算结果表明,与 禁忌搜索是一种启发式算法21,其基本过程如下, 基于粒子群优化的属性约简算法、基于禁忌搜索的 算法1基本的禁忌搜索算法 属性约简算法和基于蚁群优化的最小属性约简算法 1)选择问题的一个初始解x0,设置禁忌表 相比,本文算法取得了较好的改进效果, (T)为空并且设迭代次数k:=0; 1基本概念和记号 2)根据禁忌限制生成一个当前解k的邻居解 空间M(x); 为叙述方便起见,首先简单回顾粗糙集理论的 3)计算邻居解空间M(xx)的最优解xk+1并且 一些基本概念10口以及禁忌搜索和粒子群优化的 更新禁忌表TL; 基本思想 4)如果满足停止条件则停止该算法,否则转向2). 1.1粗糙集与属性约简 1.3标准粒子群优化算法PS0 四元组S=(U,A,Vf)是一个信息系统,其中U 最早由Kennedy等人[Ia]提出的PS0算法是一 为对象的非空有限集合,即论域;A为属性的非空有 种群体搜索算法,它根据对环境的适应度将群体中 限集合,信息系统中A常分为条件属性C和决策属 的个体移动到好的区域。每个个体看作是D维搜索 性D;V=U'a,Va是属性的值域:f为U×A→V是 空间中的一个没有体积的微粒(点),在搜索空间中 一个信息函数,它为每个对象的每个属性赋予一个 以一定的速度飞行,这个速度根据它本身的飞行经 信息值,即Ha∈A,x∈U,f(x,a)∈V.设PCA且 验和同伴的飞行经验来动态调整.第个微粒表示 P≠☑,定义由属性子集P导出的二元关系如下: 为X:=(x1,x2,…,xD),它经历过的最好位置(有 IND(P)=(x,y)I Ya E Pf(x,a)=f(y,a). 最好的适应值)记为P:=(P,P2,…,PD),也称为 若(x,y)∈ND(P),则称x和y是P不可区分的,即 P·在群体所有微粒经历过的最好位置的索引号 依据P中所含各属性无法区分x和y 用符号g表示,即P,也称为g·微粒i的速度用 设集合XCU,P是一个等价关系,称PX为集合 V:=(,2,…,vn)表示.对每一代,它的第d维 X的P下近似集;PX为集合X的P上近似集;集合 (1≤d≤D)根据如下方程进行变化: BNp(X)为X的P边界域 vid =w x vu +c x rand()*(Pi-%u)+ PX={x|x∈U,[x]pCX}, c2×Rand()*(Pgd-xa), PX={xlx∈U,[x]pnX≠0}, 动=xa+V BNp(X)=PXPX. 式中:w为惯性权重;c1和c2为加速常数;rand()和 设P和Q为论域上的等价关系,Q的P正域记 Rand()为2个在[0,1]范围里变化的随机值, 作POSp(Q): POS(Q)=PX, 2基于禁忌搜索和粒子并行子群的属 I POS(Q)I 性约简算法TSPPSOAR k=Yp(Q)=- 1U| 称知识Q是k度依赖于知识P的,记作P→Q. 禁忌搜索算法通过搜索当前解的邻居来获得 当k=1时,称Q完全依赖于P;当0<k<1时,称Q 解,其中禁忌表有助于避免搜索陷入局部最优,但是 粗糙依赖于P;当k=0时,称Q完全独立于P. 该方法的搜索能力并不强;而粒子群优化算法可以 属性约简是去除一些冗余的属性而不诚少原来 通过粒子群来搜索解,具有较强的搜索能力,但是容 集合的分类质量.一个约简可以定义如下: 易陷入局部最优.本文通过结合这2种算法的思想 Red =RCI YR(D)=Yc(C), 来提高搜索能力并避免陷入局部最优,由此提出了 HBCR,YB(D)≠Ac(D)i. 一个改进的算法,记为TSPPSOAR.该算法将原始 一个数据集可能有多个属性约简,最小约简是 粒子群分解成具有较少个体数目的并行子群来提高

·134 智能系统学报 第6卷 获得最优解的概率,同时利用了带有长期记忆的禁 位置不一致的位上随机取V位置为相同.更新后该粒 忌策略和2个优化方案来提高小群体数目的子群的 子仍然保持着自身到全局最优位置的搜索能力. 搜索能力. 2)如果V>x。,先将当前粒子位置更新为与全局 一般地,基本的禁忌搜索算法仅利用了短期记忆 所经历最优位置相同,再在更新前粒子的位置和全局 即禁忌表.为了取得更好的性能,需要长期记忆来保存 所经历最优位置相同的位上随机抽取置(Vx)位置为 搜索过程中获得的重要特征.因此,在本文算法的禁忌 不同,这样粒子在到达当前全局最优位置之前还可以 搜索过程中加入了长期记忆“属性的使用频率”,并通 继续保持朝其他方向飞行搜索的能力, 过如下的2个方案来自动调节解的状态, 3)如果改变位置后粒子的位置在T,表中出现, 多样性:通过属性的使用频率来调节解,使算法 则重新执行1)、2)来生成新的位置, 在解空间搜索到新的区域。 2.5粒子的位置质量衡量标准 增强性:提高一些有较好前景(有可能达到全 算法中使用适应值来衡量粒子的位置解的质量 局最优点)的解的优先权,以搜索该类较优解周围 优劣,适应度函数如下所示4: 可能存在的更优解。 Fitness =a x(D)+Bx CI-RI I CI (1) 2.1粒子的解表示 TSPPSOAR利用二进制串来表示一个解(粒子 式中:Yr(D)是属性R相对于决策属性D的依赖 的位置).如果对于一个解x中的某个属性x(i=1, 度;R|是被选择的子集的属性个数;a和B分别控 2,…,1C1,1C1为所有条件属性的个数)的值为1, 制着依赖度的值和子集的长度,其中a取0~1的 则x具有第i个属性;同样地,如果=0,则x不具 数,B=1-a.本文中设置a为0.9,B=0.1.设置较高 有第i个属性. 的值可以尽量保证最优解本身是一个约简,而不降 2.2禁忌表 低原集合分类质量.算法的目标是最大化适应值、 禁忌表T,的作用是用来避免陷入局部最优和 2.6并行子群 避免重复生成不合适的粒子的位置解.全部为1(所 根据概率论可以得出: 有属性都被考虑)和全部为0(所有属性都不考虑) 1)如果一个粒子群A得到最优解的概率为p, 的解将长期存放在T表中.T剩余中的位置 则A陷入局部最优解的概率则为(1-p), (|TL1-2)被用于保存最近粒子到达的位置,其中 2)将A分解成n个并行子群A:,则n个A:构成 |T|表示禁忌表的长度, 一个新的群体A';在求解同一个问题时,每个子群 禁忌表的更新策略为:如果禁忌表还未存满,则 A'得到最优解的概率为卫',总群体A'陷入局部最优 将新的粒子的位置解插人禁忌表中;否则将 解的概率为(1-p)”。 (1T,|-2)中最先插入的解替换为新的解, 3)如果p'不会远小于p,则粒子群A'陷入局部 2.3粒子速度的表示 最优的概率小于粒子群A进入局部最优的概率;因 采用文献[14]的方法,每个粒子的速度被表示 此具有并行子群的总群体A'获得最优解的概率可 为[1,'x]区间内的1个正数,表示每次粒子有多 以满足如下条件:1-(1-p')”>卫. 少个位要被改变为与全局所经历最优位置相对应的 群体个数为N的粒子群有2种分解策略:一种 位置一致.2个粒子之间的差跟2个粒子的不一致 是分解为子群个数为1,则每个子群内粒子个数为 的位的个数有关4 N/n1;另一种是选择分解的群体个数n2>n1,则每 需要注意的是,算法中必须限制粒子的速度而 个子群体内粒子个数N/n2<N/n1.2种策略分别通 避免飞过全局最优解而只能找到次优解.本文中设 过增大p'和n的值来提高获得最优解的概率,对于 置Vma=(1/3)*1C1,如果V<1,则V=1. 这2种策略章节3.2都做了实验比较, 2.4粒子位置更新策略 经过分解后的粒子群具有类似于如图1的拓扑 设更新后的速度为V,当前粒子位置和全局所 结构[5],子群内部独立地搜索解空间,而子群之间 经历的最优位置Pt之间的不一致的位个数为xg, 通过全网络连接,互相交流着该子群经历过的最好 则更新策略如下所示。 的位置的信息 1)如果V<=x。,则在当前粒子和全局所经历最优

第2期 马胜蓝,等:一种带禁忌搜索的粒子并行子群最小约简算法 ·135· 3)通过设置w:=0来删除属性0:,计算y值; 4)如果y增加或者y不变(但是由于属性个数 减少)则更新Pt; 子群n 5)更新全局最优解Pe 最后的方案是约简激励.在TSPPSOAR迭代搜 索的过程中,得到的约简都被保存在一个叫做Red- Set的集合中.利用核的概念,在RedSet中取nR个 群 最优约简的交集构造一个新的解x.如果x的属 性个数比粒子全局经历的最优位置Pe的属性个数 图1 TSPPSOAR拓扑结构 至少少2个,则x中根据启发性信息将一个0的 Fig.1 The topology of TSPPSOAR 位置改为1.该方案一直执行到Xu中的属性个数 2.7多样性增强性方案 比Pt的属性少一个。 TSPPSOAR算法将粒子群分解为并行的子群,但 过程3[xBu]=EliteReducts(RedSet,nR) 是由于每个子群的群体个数的下降,必然会导致每个 1)如果RedSet为空则过程结束,否则到2); 子群的搜索能力的下降.如2.6中所述,要想降低陷 2)设nr为RedSet中最优约简的属性个数,设 入局部最优的概率,必须让子群获得最优解的概率不 置xu为RedSet中ne个最优约简的交集; 会远小于原群体获得最优解的概率,所以在子群内部 3)如果x的属性个数小于(np-1),则执行 采用额外的方案来确保每个子群的搜索能力。 4),否则过程结束; 因此,TSPPSOAR应用3种方案[刃来提高搜索 4)如果P0Sm(D)等于原论域的正域个数,则 的多样性和增强性.为描述完整起见,以下介绍这3 过程结束; 个方案,第一个方案是在一定迭代时间内无法搜索 5)在x的所有0位置中选择一个,在置为1 出可以改进现有的最优解时所执行的多样性方案。 的情况下可以得到最大的r值的位置,将其置为1, TSPPSO0AR中定义了一个具有ICI维的向量v,其 转到3). 中向量中第i维代表群体中每个粒子经历过的位置 激励过程相当于在RedSet的交集“新核”基础 中选择属性i的次数.因此一个多样性的新解x“可 上,寻找比搜索到的全局最小约简p更优的解。 以通过,中每个属性的被选择的概率来获得.以下 2.8 TSPPS0AR算法 给出x的生成过程: 基于禁忌搜索和粒子并行子群的属性约简算法 过程1[x]=Diverse(v) TSPPSOAR,将原群体分解成n个并行的子群,每个子 1)随机生成数字r1,2,…,r1c∈(0,1), 群同时进行属性约简,以提高获得最优解的概率。 2)重复执行如下步骤从i=1,2,…,1C1. 在该算法中,惯性权重W随着迭代次数的增加 3)如果>/公利则设置=1,香则设置 而不断减小,公式如下 xm=0. W=W= _Ws-W血x iter., (2) 上述的多样性方案主要选择过去较少被选择到 iterma 的属性,将粒子导向一个新的解空间,从而加大了逃 式中:Wma和Wmin为初始设定的值,iter为当前迭代 离出局部最小点的可能性, 的次数.具体算法如下, 在获得x"后,如果全局经历的最优位置Pt在 算法2 TSPPSOAR 经过一段时间后仍然没有任何改进,则TSPPSOAR 1)初始化一群粒子,包括随机的位置和速度; 应用增强性方案来改进每个粒子经历过的最优位置 初始化禁忌表T,禁忌表中包含2个位置(0,…,0) P·在过程2.2中通过对P进行约简而不减少 和(1,…,1),设置v为空向量,RedSet为空集合, Ya(D),将原解从代数协调集调整为代数约简, 迭代次数iter为O,选择lns、impabak和lin,令Inms> 过程2 Shaking(Phet) Imp>Lha>1s.将粒子群分割成n个含有相同粒子 1)对每个粒子经历的最优位置P重复执行如 数的子群(child,child2.,…,child.),每个子群维护 下步骤; 着各自的禁忌表T、 2)将Pem中的为1的属性构造成一个新的集合 2)对于每个子群child:执行3)~8). W={01,02,…,01w1}; 3)利用式(1)求出每个粒子的适应值
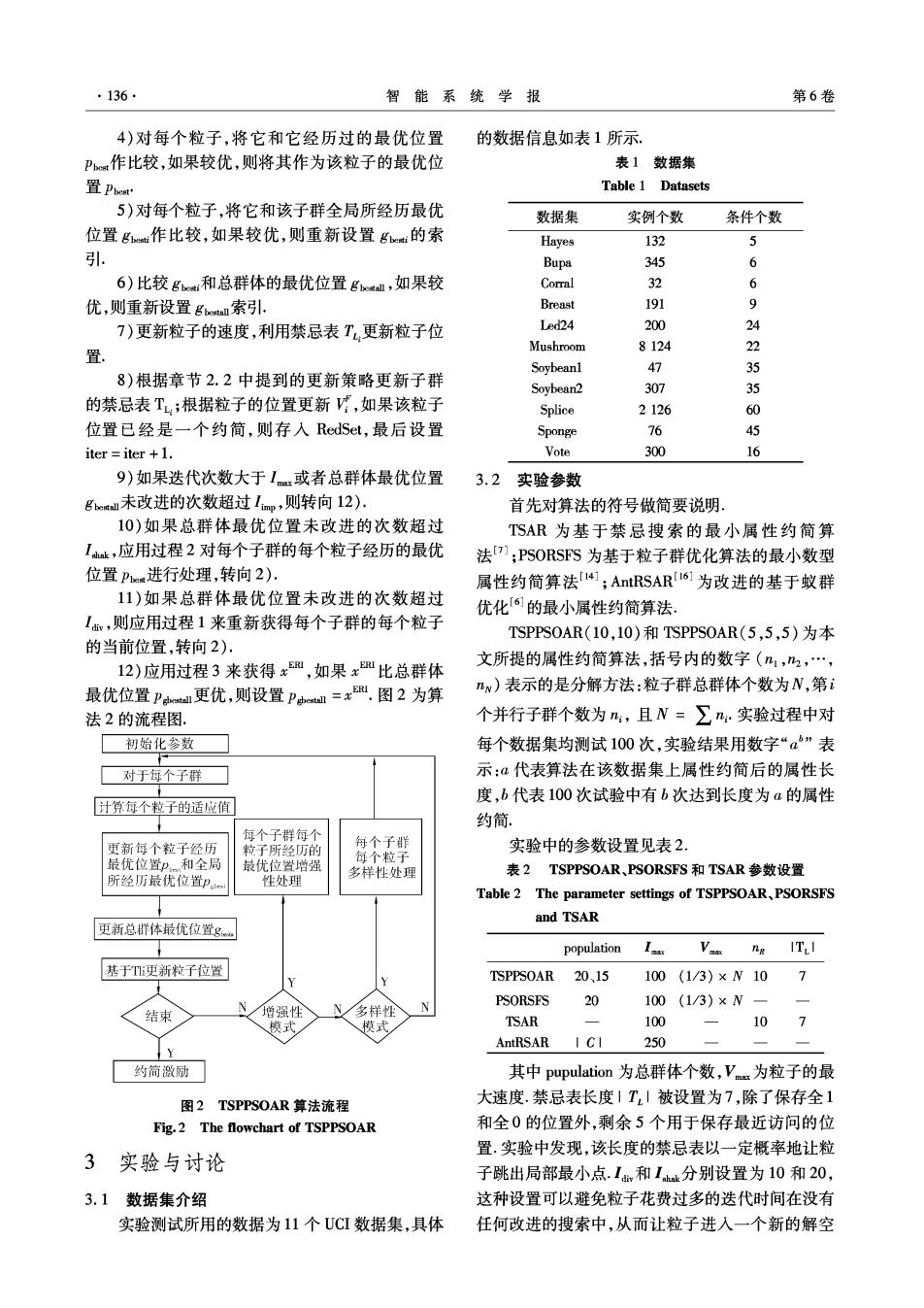
·136 智能系统学报 第6卷 4)对每个粒子,将它和它经历过的最优位置 的数据信息如表1所示. P作比较,如果较优,则将其作为该粒子的最优位 表1数据集 置Pbe Table 1 Datasets 5)对每个粒子,将它和该子群全局所经历最优 数据集 实例个数 条件个数 位置g作比较,如果较优,则重新设置ge的索 Hayes 132 5 引 Bupa 345 6 6)比较ge,和总群体的最优位置ge,如果较 Corral 32 6 优,则重新设置boeatall索引. Breast 191 9 7)更新粒子的速度,利用禁忌表T更新粒子位 Led24 200 24 置 Mushroom 8124 22 Soybeanl 47 35 8)根据章节2.2中提到的更新策略更新子群 Soybean2 307 35 的禁忌表T,;根据粒子的位置更新,如果该粒子 Splice 2126 60 位置已经是一个约简,则存人RedSet,最后设置 Sponge 76 45 iteriter +1. Vote 300 16 9)如果迭代次数大于I或者总群体最优位置 3.2实验参数 ge未改进的次数超过Ip,则转向12) 首先对算法的符号做简要说明. 10)如果总群体最优位置未改进的次数超过 TSAR为基于禁忌搜索的最小属性约简算 I业,应用过程2对每个子群的每个粒子经历的最优 法7];PSORSFS为基于粒子群优化算法的最小数型 位置Pe进行处理,转向2) 属性约简算法[4;AntRSAR6I为改进的基于蚁群 11)如果总群体最优位置未改进的次数超过 优化[6的最小属性约简算法。 I,则应用过程1来重新获得每个子群的每个粒子 TSPPS0AR(10,10)和TSPPS0AR(5,5,5)为本 的当前位置,转向2). 12)应用过程3来获得x,如果x比总群体 文所提的属性约简算法,括号内的数字(m1,2,…, 最优位置p更优,则设置pe=xu.图2为算 nw)表示的是分解方法:粒子群总群体个数为N,第i 法2的流程图. 个并行子群个数为n,且N=∑n,实验过程中对 初始化参数 每个数据集均测试100次,实验结果用数字“a”表 对于每个子群 示:代表算法在该数据集上属性约简后的属性长 度,b代表100次试验中有b次达到长度为a的属性 计算:每个粒子的适应值 约简. 每个子群每个 更新每个粒子经历 粒子所经历的 每个子群 实验中的参数设置见表2. 每个粒子 最优位置p和全局 最优位置增强 所经历最优位置pc 多样性处理 表2 TSPPSOAR、PSORSFS和TSAR参数设置 性处理 Table 2 The parameter settings of TSPPSOAR,PSORSFS and TSAR 更新总体最优位置g population V ng ITI 基于T更新粒子位性 TSPPS0AR20、15 100(1/3)×N10 7 t N PSORSFS 20 100(1/3)×N 结東 增强性 N 多样性 模式 模式 TSAR 100 10 1 AntRSAR 250 约简激励 其中pupulation为总群体个数,Vam为粒子的最 图2 TSPPSOAR算法流程 大速度.禁忌表长度1T|被设置为7,除了保存全1 Fig.2 The flowchart of TSPPSOAR 和全0的位置外,剩余5个用于保存最近访问的位 置.实验中发现,该长度的禁忌表以一定概率地让粒 3实验与讨论 子跳出局部最小点.I,和Ih.分别设置为10和20, 3.1数据集介绍 这种设置可以避免粒子花费过多的迭代时间在没有 实验测试所用的数据为11个UCI数据集,具体 任何改进的搜索中,从而让粒子进入一个新的解空