
随机现象的认知模型 ,两个随机事件(1)一一观测对象Ω 。先验概率一 所观测事件发生的概率 。对观测者而言,先验概率具有客观性,不受观测者的意志 而改变
两个随机事件 (1) ——观测对象 Ω ◦ 先验概率——所观测事件发生的概率 ◦ 对观测者而言,先验概率具有客观性,不受观测者的意志 而改变
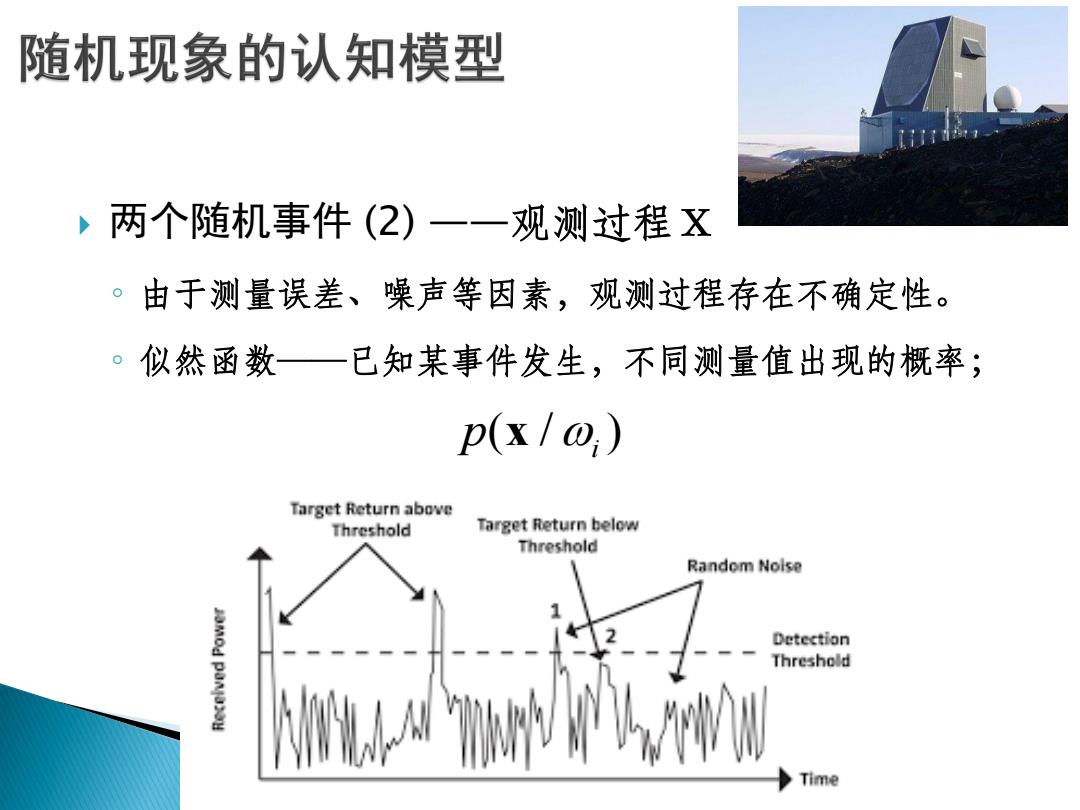
随机现象的认知模型 ,两个随机事件(2)一一观测过程X 。由于测量误差、噪声等因素,观测过程存在不确定性。 。似然函数一已知某事件发生,不同测量值出现的概率; p(x/@,) Target Return above Threshold Target Return below Threshold Random Noise JMOd panja3oy Detection Threshold Time
两个随机事件 (2) ——观测过程 X ◦ 由于测量误差、噪声等因素,观测过程存在不确定性。 ◦ 似然函数——已知某事件发生,不同测量值出现的概率; ( / )i p x

随机现象的认知模型 ,贝叶斯推断: P(x)=∑px/@,)P(@,) i 。后验概率(Posteriori Probability)一 一已知观测结果和似然 函数,推断观测对象出现的概率; P(@;/x) 。贝叶斯定理: P(o,IX)P(x)=P(K,0)=p(X/0)P(O,) →P(0,/x)= P(x,o,)_p(x/o,)P(o,) P(x) P(x)
贝叶斯推断: ◦ 后验概率(Posteriori Probability)——已知观测结果和似然 函数,推断观测对象出现的概率; ◦ 贝叶斯定理: ( / ) P i x ( / ) ( ) ( , ) ( / ) ( / ) ( ) ( / ( ) ( , ) ( ) ( ) ) i i i i i i i i P P p P P P P p P P P x x x x x x x x x 1 ( ) ( / ) ( ) n i i i P p P x x

贝叶斯推断 ,例:已知1000人中有1人得病,进行测试,如果有病,则该测试 结果为阳性的概率为0.99,无病,测试结果为阳性的概率为0.02, 某人测试结果为阳性,问其得病概率为多少? P(+/)=0.99,P(-/)=0.01, P(+/H)=0.02,P(-/H)=0.98, P()=0.001,P(H)=0.999 P(I,+) P(+/I)P(I) P(I/+)= P(+) P(+/)P()+P(+/H)P(H) 0.99×0.001 =0.0472 0.99×0.001+0.02×0.999
例:已知1000人中有1人得病,进行测试,如果有病,则该测试 结果为阳性的概率为0.99,无病,测试结果为阳性的概率为0.02, 某人测试结果为阳性,问其得病概率为多少? ( / ) 0.99, (- / ) 0.01, ( / ) 0.02, (- / ) 0.98, ( ) 0.001, ( ) 0.999 P I P I P H P H P I P H ( , ) ( / ) ( ) ( / ) ( ) ( / ) ( ) ( / ) ( ) 0.99 0.001 0.0472 0.99 0.001 0.02 0.999 P I P I P I P I P P I P I P H P H
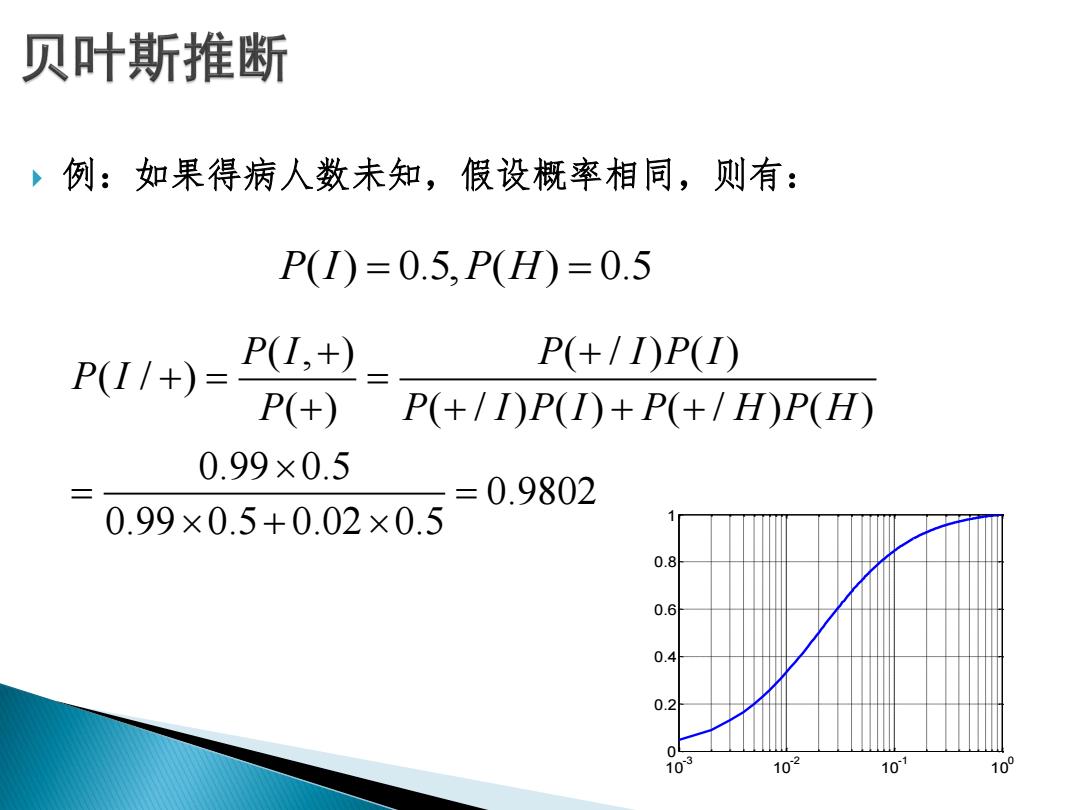
贝叶斯推断 例:如果得病人数未知,假设概率相同,则有: P()=0.5,P(H)=0.5 P(I,+) P+/DP( P(I/+)= P(+) P(+/I)P(I)+P(+/H)P(H) 0.99×0.5 =0.9802 0.99×0.5+0.02×0.5 0.8 0.6 0.4 0.2 04 103 102 107 10°
例:如果得病人数未知,假设概率相同,则有: P I P H ( ) 0.5, ( ) 0.5 ( , ) ( / ) ( ) ( / ) ( ) ( / ) ( ) ( / ) ( ) 0.99 0.5 0.9802 0.99 0.5 0.02 0.5 P I P I P I P I P P I P I P H P H 10-3 10-2 10-1 100 0 0.2 0.4 0.6 0.8 1