
1.3统计学习方法三要素 (3)绝对损失函数(absolute loss function) L(Y,f(X)=IY-f(X)川 (1.11) (4)对数损失函数(logarithmic loss function)或对数似然损失函数(Iog--likelihood loss function) L(Y,P(YX))=-log P(Y X) (1.12) 损失函数值越小,模型就越好。由于模型的输入、输出(X,Y)是随机变量,遵循 联合分布P(X,Y),所以损失函数的期望是 Rexp(f)=EplL(Y,f(X))] (w()P(.rd (1.13) 这是理论上模型f(X)关于联合分布P(X,Y)的平均意义下的损失,称为风险函 数(risk function)或期望损失(expected loss)。 学习的日标就是选择期望风险最小的模型。由于联合分布P(X,Y)是未知 的,Rxp()不能直接计算。实际上,如果知道联合分布P(X,Y),可以从联合分布 直接求出条件概率分布P(YX),也就不需要学习了。正因为不知道联合概率分布, 所以才需要进行学习。这样一来,一方面根据期望风险最小学习模型要用到联合分 布,另一方面联合分布又是未知的,所以监督学习就成为一个病态问题(l-formed problem)。 给定一个训练数据集 T={(c1,h),(2,2),·,(cN,yN)} 模型f(X)关于训练数据集的平均损失称为经验风险(empirical risk)或经验损 失(empirical loss),记作Remp: Rm=fe》 1 (1.14 期望风险Rxp()是模型关于联合分布的期望损失,经验风险Remp()是模型 关于训练样本集的平均损失。根据大数定律,当样本容量N趋于无穷时,经验风险 Remp(f)趋于期望风险Rexp()。所以一个很自然的想法是用经验风险估计期望风险。 但是,由于现实中训练样本数目有限,甚至很小,所以用经验风险估计期望风险常常 并不理想,要对经验风险进行一定的矫正。这就关系到监督学习的两个基本策略:经 验风险最小化和结构风险最小化

18 第1章统计学习及监督学习概论 2.经验风险最小化与结构风险最小化 在假设空间、损失函数以及训练数据集确定的情况下,经验风险函数式(1.14)就 可以确定。经验风险最小化(empirical risk minimization,ERM)的策略认为,经验 风险最小的模型是最优的模型。根据这一策略,按照经验风险最小化求最优模型就是 求解最优化问题: 聘∑,fe》 (1.15) 其中,下是假设空间。 当样本容量足够大时,经验风险最小化能保证有很好的学习效果,在现实中被厂 泛采用。比如,极大似然估计(maximum likelihood estimation)就是经验风险最小 化的一个例子。当模型是条件概率分布、损失函数是对数损失函数时,经验风险最小 化就等价于极大似然估计。 但是,当样本容量很小时,经验风险最小化学习的效果就未必很好,会产生“过拟 合”(over-fitting)现象 结构风险最小化(structural risk minimization,SRM)是为了防止过拟合而提出 来的策略。结构风险最小化等价于正则化(regularization)。结构风险在经验风险上加 上表示模型复杂度的正则化项(regularizer)或罚项(penalty term)。在假设空间、损 失函数以及训练数据集确定的情况下,结构风险的定义是: Rm=六∑6fe》+A0 (1.16) 其中J()为模型的复杂度,是定义在假设空间下上的泛函。模型∫越复杂,复杂度 J()就越大:反之,模型f越简单,复杂度J()就越小。也就是说,复杂度表示了对 复杂模型的惩罚。入≥0是系数,用以权衡经验风险和模型复杂度。结构风险小需要经 验风险与模型复杂度同时小。结构风险小的模型往往对训练数据以及未知的测试数据 都有较好的预测。 比如,贝叶斯估计中的最大后验概率估计(maximum posterior probability esti- mation,MAP)就是结构风险最小化的一个例子。当模型是条件概率分布、损失函数 是对数损失函数、模型复杂度由模型的先验概率表示时,结构风险最小化就等价于最 大后验概率估计 结构风险最小化的策略认为结构风险最小的模型是最优的模型。所以求最优模 型,就是求解最优化问题: CL(,f()》+λJ(f) (1.17)

1.4模型评估与模型选择 19 这样,监督学习问题就变成了经验风险或结构风险函数的最优化问题(1.15)和 (117)。这时经验或结构风险函数是最优化的目标函数。 1.3.3算法 算法是指学习模型的具体计算方法。统计学习基于训练数据集,根据学习策略, 从假设空间中选择最优模型,最后需要考虑用什么样的计算方法求解最优模型。 这时,统计学习问题归结为最优化问题,统计学习的算法成为求解最优化问题的 算法。如果最优化问题有显式的解析解,这个最优化问题就比较简单。但通常解析解 不存在,这就需要用数值计算的方法求解。如何保证找到全局最优解,并使求解的过 程非常高效,就成为一个重要问题。统计学习可以利用已有的最优化算法,有时也需 要开发独自的最优化算法。 统计学习方法之间的不同,主要来自其模型、策略、算法的不同。确定了模型、策 略、算法,统计学习的方法也就确定了。这就是将其称为统计学习方法三要素的原因。 以下介绍监督学习的几个重要概念。 1.4模型评估与模型选择 1.4.1训练误差与测试误差 统计学习的目的是使学到的模型不仅对已知数据而且对未知数据都能有很好的 预测能力。不同的学习方法会给出不同的模型。当损失函数给定时,基于损失函数的 模型的训练误差(training error)和模型的测试误差(test error)就自然成为学习方 法评估的标准。注意,统计学习方法具体采用的损失函数未必是评估时使用的损失函 数。当然,让两者一致是比较理想的。 假设学习到的模型是Y=X),训练误差是模型Y=(X)关于训练数据集的 平均损失: Ran=立e,fz》 (1.18) 其中N是训练样本容量。 测试误差是模型Y=(X)关于测试数据集的平均损失: (1.19) L= 其中N'是测试样本容量

20 第1章统计学习及监督学习概论 例如,当损失函数是0-1损失时,测试误差就变成了常见的测试数据集上的误差 率(error rate) N ∑≠红,》 eut= (1.20) 这里I是指示函数(indicator function),即y≠f(x)时为l,否则为0。 相应地,常见的测试数据集上的准确率(accuracy)为 >I(vi=f(z:)) (1.21)) 显然, Ttest +etest =1 训练误差的大小,对判断给定的问题是不是一个容易学习的问题是有意义的,但 本质上不重要。测试误差反映了学习方法对未知的测试数据集的预测能力,是学习中 的重要概念。显然,给定两种学习方法,测试误差小的方法具有更好的预测能力,是 更有效的方法。通常将学习方法对未知数据的预测能力称为泛化能力(generalization ability),这个问题将在1.6节继续论述。 1.4.2过拟合与模型选择 当假设空间含有不同复杂度(例如,不同的参数个数)的模型时,就要面临模型选 择(model selection)的问题。我们希望选择或学习一个合适的模型。如果在假设空间 中存在“真”模型,那么所选择的模型应该逼近真模型。具体地,所选择的模型要与真 模型的参数个数相同,所选择的模型的参数向量与真模型的参数向量相近。 如果一味追求提高对训练数据的预测能力,所选模型的复杂度则往往会比真模型 更高。这种现象称为过拟合(over-fitting)。过拟合是指学习时选择的模型所包含的参 数过多,以至出现这一模型对已知数据预测得很好,但对未知数据预测得很差的现象。 可以说模型选择旨在避免过拟合并提高模型的预测能力。 下面,以多项式函数拟合问题为例,说明过拟合与模型选择。这是一个回归问题。 例1.1假设给定一个训练数据集①: T={(x1,h),(x2,2),·,(xN,w)} 其中,x∈R是输入x的观测值,∈R是相应的输出y的观测值,i=1,2,·,N。 ①本例米自参考文献2②
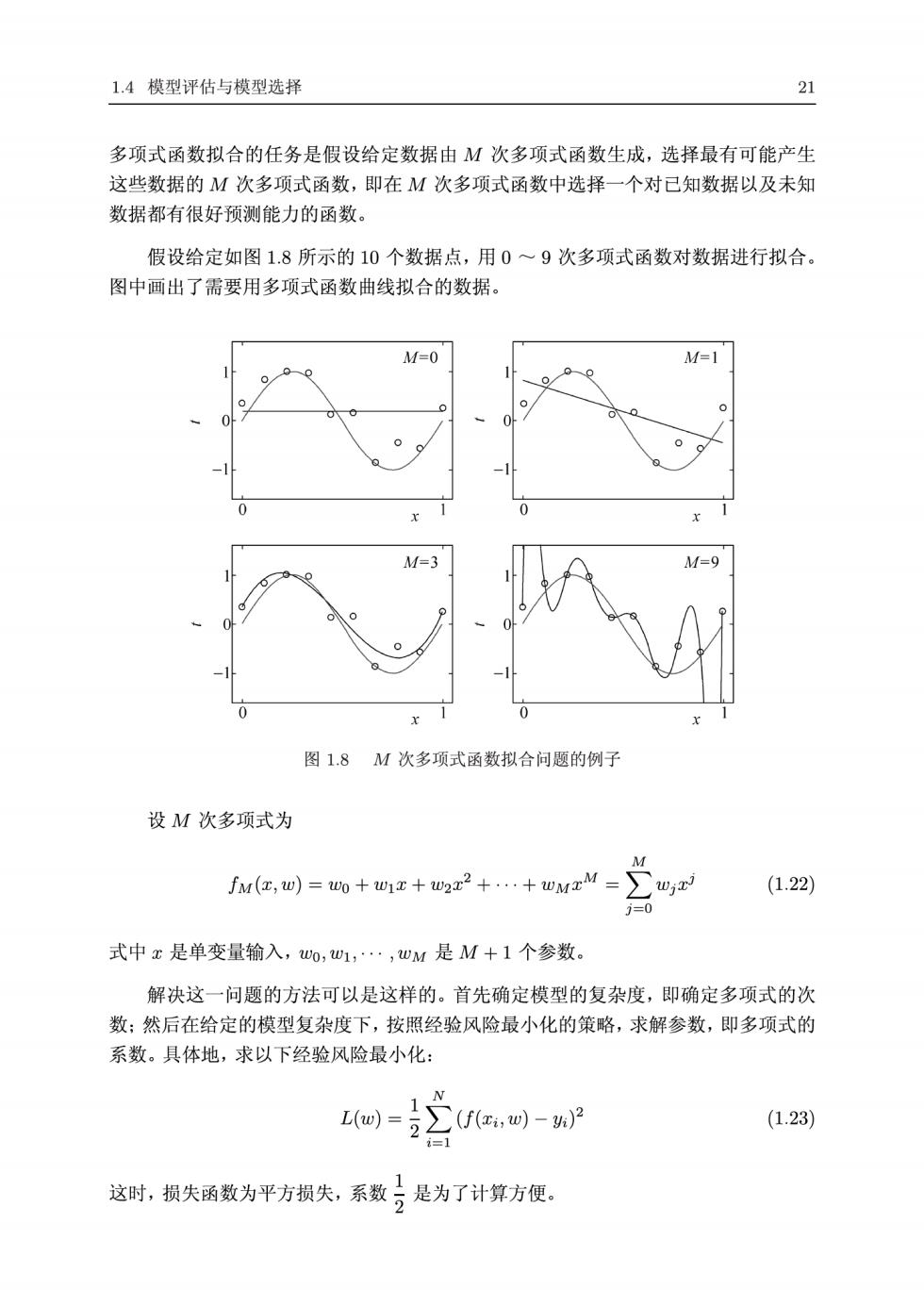
1.4模型评估与模型选择 21 多项式函数拟合的任务是假设给定数据由M次多项式函数生成,选择最有可能产生 这些数据的M次多项式函数,即在M次多项式函数中选择一个对已知数据以及未知 数据都有很好预测能力的函数。 假设给定如图1.8所示的10个数据点,用0~9次多项式函数对数据进行拟合。 图中画出了需要用多项式函数曲线拟合的数据。 M=0 M=1 V= 图1.8M次多项式函数拟合问题的例子 设M次多项式为 fM(红,四))=o+01x+u2z2++wMxM=∑ (1.22) 式中x是单变量输入,0,w1,·,wM是M+1个参数。 解决这一问题的方法可以是这样的。首先确定模型的复杂度,即确定多项式的次 数:然后在给定的模型复杂度下,按照经验风险最小化的策略,求解参数,即多项式的 系数。具体地,求以下经验风险最小化: )=2∑Ue,四)-2 (1.23) 1 这时,损失函数为平方损失,系数号是为了计算方便