
1.2统计学习的分类 输入变量X和输出变量Y有不同的类型,可以是连续的,也可以是离散的。人 们根据输入输出变量的不同类型,对预测任务给予不同的名称:输入变量与输出变量 均为连续变量的预测问题称为回归问题;输出变量为有限个离散变量的预测问题称为 分类问题:输入变量与输出变量均为变量序列的预测问题称为标注问题。 (2)联合概率分布 监督学习假设输入与输出的随机变量X和Y遵循联合概率分布P(X,Y). P(X,Y)表示分布函数,或分布密度函数。注意在学习过程中,假定这一联合概率分 布存在,但对学习系统来说,联合概率分布的具体定义是未知的。训练数据与测试数 据被看作是依联合概率分布P(X,Y)独立同分布产生的。统计学习假设数据存在一定 的统计规律,X和Y具有联合概率分布就是监督学习关于数据的基本假设。 (3)假设空间 监督学习的目的在于学习一个由输入到输出的映射,这一映射由模型来表示。换 句话说,学习的目的就在于找到最好的这样的模型。模型属于由输入空间到输出空间 的映射的集合,这个集合就是假设空间(hypothesis space)。假设空间的确定意味着 学习的范围的确定。 监督学习的模型可以是概率模型或非概率模型,由条件概率分布P(YX)或决策 函数(decision function)Y=f(X)表示,随具体学习方法而定。对具体的输入进行 相应的输出预测时,写作P(yx)或y=f(x)。 (4)问题的形式化 监督学习利用训练数据集学习一个模型,再用模型对测试样本集进行预测。由于 在这个过程中需要标注的训练数据集,而标注的训练数据集往往是人工给出的,所以 称为监督学习。监督学习分为学习和预测两个过程,由学习系统与预测系统完成,可 用图1.1来描述。 V)2)x) 学习系统 模型 P(vlx) v-f(x) 预测系统 图1.1监督学习 首先给定一个训练数据集 T={(c1,h),(a2,2),…,(xN,yN)}

第1章统计学习及监督学习概论 其中(1,),i=1,2,·,N,称为样本或样本点。1∈XCRn是输入的观测值,也 称为输入或实例,班∈y是输出的观测值,也称为输出 监督学习分为学习和预测两个过程,由学习系统与预测系统完成。在学习过程中, 学习系统利用给定的训练数据集,通过学习(或训练)得到一个模型,表示为条件概率 分布P(YX)或决策函数Y=f(X)。条件概率分布P(YX)或决策函数Y=(X) 描述输入与输出随机变量之间的映射关系。在预测过程中,预测系统对于给定的测试 样本集中的输入xN+1,由模型N+1=arg max P(c+1)或N+1=fN+1)给出 相应的输出N+1 在监督学习中,假设训练数据与测试数据是依联合概率分布P(X,Y)独立同分布 产生的。 学习系统(也就是学习算法)试图通过训练数据集中的样本(工,)带来的信息 学习模型。具体地说,对输入,一个具体的模型y=f(x)可以产生一个输出f(x), 而训练数据集中对应的输出是:。如果这个模型有很好的预测能力,训练样本输出 和模型输出f()之间的差就应该足够小。学习系统通过不断地尝试,选取最好的模 型,以便对训练数据集有足够好的预测,同时对未知的测试数据集的预测也有尽可能 好的推广。 2.无监督学习 无监督学习O(unsupervised learning)是指从无标注数据中学习预测模型的机器 学习问题。无标注数据是自然得到的数据,预测模型表示数据的类别、转换或概率。无 监督学习的本质是学习数据中的统计规律或潜在结构。 模型的输入与输出的所有可能取值的集合分别称为输入空间与输出空间。输入空 间与输出空间可以是有限元素集合,也可以是欧氏空间。每个输入是一个实例,由特 征向量表示。每一个输出是对输入的分析结果,由输入的类别、转换或概率表示。模 型可以实现对数据的聚类、降维或概率估计。 假设X是输入空间,2是隐式结构空间。要学习的模型可以表示为函数z=9(x), 条件概率分布P(x),或者条件概率分布P(xz)的形式,其中x∈X是输入,之∈2 是输出。包含所有可能的模型的集合称为假设空间。无监督学习旨在从假设空间中选 出在给定评价标准下的最优模型。 无监督学习通常使用大量的无标注数据学习或训练,每一个样本是一个实例。训 练数据表示为U={1,2,…,xN},其中x,i=1,2,…,N,是样本。 无监督学习可以用于对已有数据的分析,也可以用于对未来数据的预测。分 析时使用学习得到的模型,即函数z=(x),条件概率分布P(),或者条件概率 分布P()。预测时,和监督学习有类似的流程。由学习系统与预测系统完成,如 ①也译作非监督学习
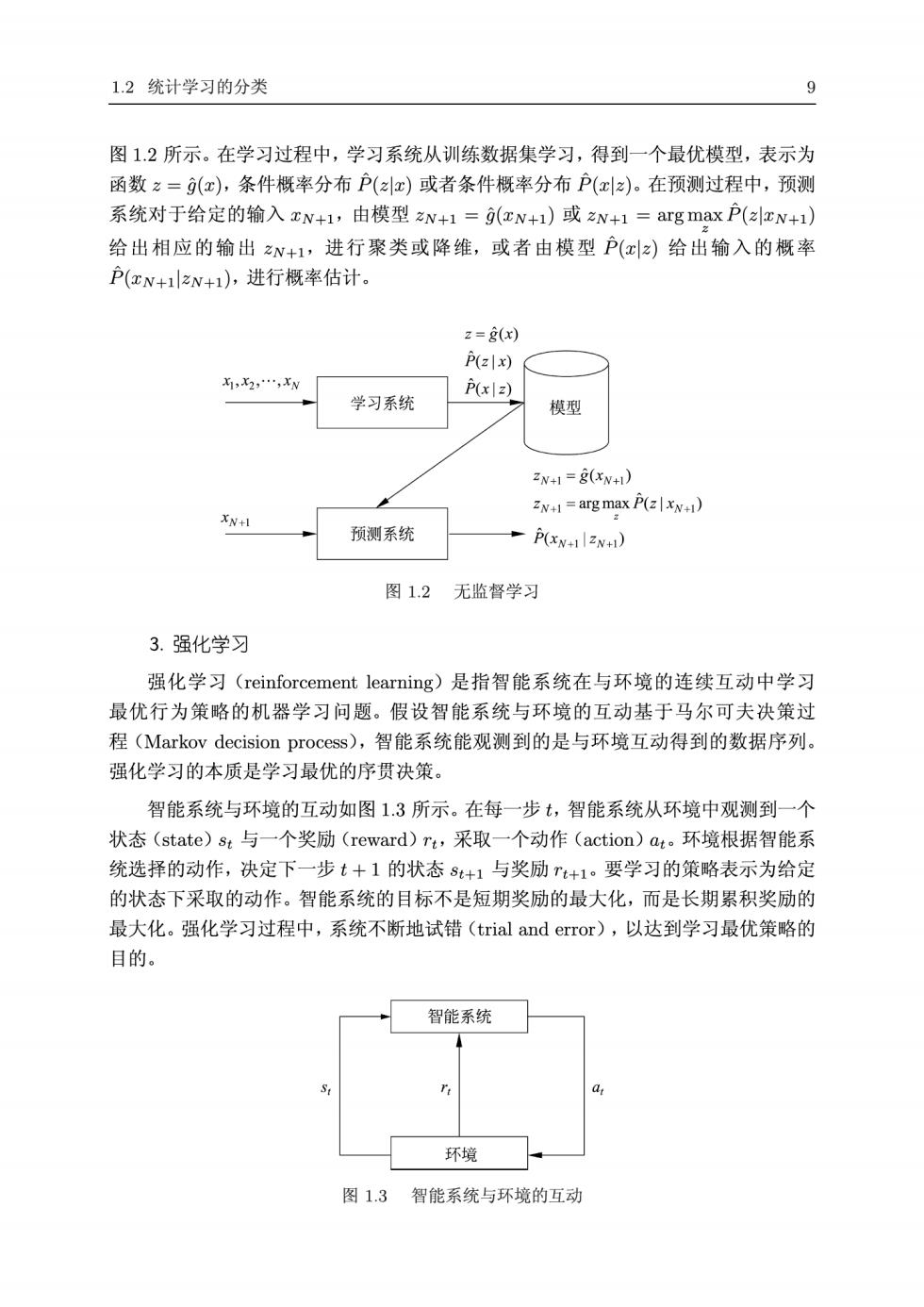
1.2统计学习的分类 图1.2所示。在学习过程中,学习系统从训练数据集学习,得到一个最优模型,表示为 函数z=(x,条件概率分布户()或者条件概率分布户(x)。在预测过程中,预测 系统对于给定的输入xN+1,由模型zN+1=rN+1)或zN+1=arg maxP(azN+1) 给出相应的输出N+1,进行聚类或降维,或者由模型P()给出输入的概率 P(xN+zN+1),进行概率估计。 2=(x) lx) P(xlz) 学习系统 模型 N1=(N) XN+1 2w1=arg max P(4) 预测系统 P() 图1.2无监督学习 3.强化学习 强化学习(reinforcement learning)是指智能系统在与环境的连续互动中学习 最优行为策略的机器学习问题。假设智能系统与环境的互动基于马尔可夫决策过 程(Markov decision process).,智能系统能观测到的是与环境互动得到的数据序列。 强化学习的本质是学习最优的序贯决策。 智能系统与环境的互动如图1.3所示。在每一步t,智能系统从环境中观测到一个 状态(state)st与一个奖励(reward)rt,采取一个动作(action)at。环境根据智能系 统选择的动作,决定下一步t+1的状态st+1与奖励+1。要学习的策略表示为给定 的状态下采取的动作。智能系统的目标不是短期奖励的最大化,而是长期累积奖励的 最大化。强化学习过程中,系统不断地试错(trial and error),以达到学习最优策略的 目的。 智能系统 环境 图1.3智能系统与环境的互动

10 第1章统计学习及监督学习概论 强化学习的马尔可夫决策过程是状态、奖励、动作序列上的随机过程,由五元组 (S,A,P,r,)组成。 。S是有限状态(state)的集合 ·A是有限动作(action)的集合 ·P是状态转移概率(transition probability)函数: P(s's,a)=P(st+1=s'st=s,at=a) ·r是奖励函数(reward function):r(s,a)=E(r+ist=s,at=a) ·y是衰减系数(discount factor):Y∈[0,1 马尔可夫决策过程具有马尔可夫性,下一个状态只依赖于前一个状态与动作,由 状态转移概率函数P(s|s,a)表示。下一个奖励依赖于前一个状态与动作,由奖励函 数r(8,a)表示。 策略π定义为给定状态下动作的函数a=f(s)或者条件概率分布P(as)。给定 一个策略π,智能系统与环境互动的行为就已确定(或者是确定性的或者是随机性 的)。 价值函数(value function)或状态价值函数(state value function)定义为策略T 从某一个状态s开始的长期累积奖励的数学期望: V(8)=Ex(rt+1+yrt+2+y2r+3+...st =8] (1.1) 动作价值函数(action value function)定义为策略的从某一个状态s和动作a 开始的长期累积奖励的数学期望: q(s,a)=Enrt+1+yTt+2+yrt+3+…lst=s,at=dl (1.2) 强化学习的目标就是在所有可能的策略中选出价值函数最大的策略π,而在实际 学习中往往从具体的策略出发,不断优化已有策略。这里Y表示未来的奖励会有衰减。 强化学习方法中有基于策略的(policy-based)、基于价值的(value--based),这两 者属于无模型的(model--free)方法,还有有模型的(model--based)方法。 有模型的方法试图直接学习马尔可夫决策过程的模型,包括转移概率函数 P(s|s,a)和奖励函数r(s,a)。这样可以通过模型对环境的反馈进行预测,求出价值函 数最大的策略π*。 无模型的、基于策略的方法不直接学习模型,而是试图求解最优策略π·,表示为 函数a=f(s)或者是条件概率分布P*(als),这样也能达到在环境中做出最优决策的

1.2统计学习的分类 11 目的。学习通常从一个具体策略开始,通过搜索更优的策略进行。 无模型的、基于价值的方法也不直接学习模型,而是试图求解最优价值函数,特 别是最优动作价值函数g(s,)。这样可以间接地学到最优策略,根据该策略在给定的 状态下做出相应的动作。学习通常从一个具体价值函数开始,通过搜索更优的价值函 数进行。 4.半监督学习与主动学习 半监督学习(semi-supervised learning)是指利用标注数据和未标注数据学习预 测模型的机器学习问题。通常有少量标注数据、大量未标注数据,因为标注数据的构 建往往需要人工,成本较高,未标注数据的收集不需太多成本。半监督学习旨在利用 未标注数据中的信息,辅助标注数据,进行监督学习,以较低的成本达到较好的学习 效果。 主动学习(active learning)是指机器不断主动给出实例让教师进行标注,然后利 用标注数据学习预测模型的机器学习问题。通常的监督学习使用给定的标注数据,往 往是随机得到的,可以看作是“被动学习”,主动学习的目标是找出对学习最有帮助的 实例让教师标注,以较小的标注代价,达到较好的学习效果。 半监督学习和主动学习更接近监督学习。 1.2.2按模型分类 统计学习或机器学习方法可以根据其模型的种类进行分类。 1.概率模型与非概率模型 统计学习的模型可以分为概率模型(probabilistic model)和非概率模型(non probabilistic model)或者确定性模型(deterministic model)。在监督学习中,概率模 型取条件概率分布形式P(y),非概率模型取函数形式y=∫(),其中x是输入,y 是输出。在无监督学习中,概率模型取条件概率分布形式P(2z)或P(x2),非概率模 型取函数形式之=9(x),其中x是输入,名是输出。在监督学习中,概率模型是生成模 型,非概率模型是判别模型。 本书介绍的决策树、朴素贝叶斯、隐马尔可夫模型、条件随机场、概率潜在语 义分析、潜在狄利克雷分配、高斯混合模型是概率模型。感知机、支持向量机、k近 邻、AdaBoost、k均值、潜在语义分析,以及神经网络是非概率模型。逻辑斯谛回归既 可看作是概率模型,又可看作是非概率模型。 条件概率分布P(x)和函数y=f(x)可以相互转化(条件概率分布P(zz)和 函数之=9(x)同样可以)。具体地,条件概率分布最大化后得到函数,函数归一化后 得到条件概率分布。所以,概率模型和非概率模型的区别不在于输入与输出之间的映