
·24. 第2章分析化学中的误差和统计学处理 的分析结果得出,然而实际只能采用这种“管窥蠡测”式的分析策略。需要考虑的问题是,如 何基于局部信息,对研究对象整体做出尽量可靠的结论。 解决上述问题的数理统计方法是抽样分布。 抽样分布也解决从整体到局部的问题。实际分析中,通常对某个量进行多次测量,获得多个 测量值,如,2,x:分析结果通常是这些测量值的综合,如平均值x,而不会直接使用单个 测量值。测量值x,2,.,x,可以视为某随机变量X的n个取值。随机变量X服从某种分布(如最 常见的正态分布),但是来自X的部分取值(测量值)的x并不服从同样的分布,尽管二者存在联系 那么,如何从X的分布获得x的分布就是抽样分布要解决的另一类问题。 在数理统计中,研究对象的所有可能取值构成了一个集合,称为总体(population),这些取 值称为个体((individual)。总体包含大量甚至无限的个体。通过简单抽样①,从总体抽取有限数 量的个体构成的集合称为样本(sample),其中个体数量称为样本容量。 欲根据样本推测总体,必须将分散在样本个体中的关于总体的信息以一定的方式进行综 合,这种综合方式就是构造样本统计量(statistic)。样本统计量有多种,如样本均值、样本方差 以及其他样本矩(k阶原点矩、k阶中心矩)等,适用于不同的数理统计问题。样本统计量完全 由样本信息确定,不能包含任何总体参数。 总体通过随机变量来表征,该随机变量的分布以及数字特征就是总体的分布及其数字特 征,常见的数字特征有总体均值、总体方差等。样本统计量也是随机变量,其概率分布称为抽 样分布(sampling distribution)。如果能够从总体的分布得出样本统计量的分布,那么这种情况 称为精确抽样分布。精确抽样分布大多从正态总体得到,这就是著名的统计三大分布一分 布、分布和F分布。精确抽样分布适用于样本容量较小的数理统计问题,因此成为少量实验 数据的重要处理工具。 尽管袖样分布的解决问题模式是由局部推析整体或者从整体得出后局哥部,但是不应该视为数 学中的归纳或者演绎。数学的结论基于自洽的体系和严密的推理,而数理统计的结论来自估计, 必然包含不确定性。 5.抽样分布之样本均值的分布 设总体X一N4σ,名,X,.,X是来自该总体的一个样本,以X表示样本均值,那么 一)如果定文随机变量0 U=X-严n 那么,U~N0,1). 实际上,无论总体(数字特征:均值4,方差。)服从何种分布,只要样本容量n足够大,样本 均值灭就近似服从正态分布N(4gm):样本容量越大,近似程度越好,这是中心极限定理(central limit theorem)。对于总体分布未知的抽样问题,中心极限定理提供了一种有效的解决方式。 ①简单抽样是指抽样随机(所有个体被抽中的概率相同)和抽样独立(抽样结果互不影响

2.3数理统计基础知识 ·25. 6.抽样分布之2分布 设总体X一(山σ),X,X,.,X是来自该总体的一个样本,那么以下形式的随机变量 服从自由度(degrees of freedom,df)为ff=n-l)的,2分布(Chi-squared distribution),记作? x( x2=n-1)s2 式中,2表示样本方差。 X分布的PDF为 1 2。≥0 pmn-r( 0 (x<0) 式中,厂表示伽玛函数(gamma function)°,可用Matlab库函数gamma进行计算。 X分布的CDF为 x f P(x:S)= 八22 (x≥0) 式中,Y表示不完全伽玛函数(incomplete gamma function)。X2分布的CDF是正则化不完全伽 玛函数(regularized incomplete gamma function),可以采用Matlab库函数gammainc进行计算 分布CDF的Matlab计算程序可以参考附录1程序1.3。 有些情况下,需要计算ICDF,即计算指定累积分布概率P(如95%、99%等)对应的随机变 量取值x,这可以通过CDF的反函数求出。以Matlab代码为例,计算方法如下 -2gammaincinv. 式中,gammaincinv为Matlab库函数,用于计算正则化不完全伽玛函数的反函数。 之分布ICDF的Matlab计算程序可以参考附录1程序1.4。 图2.4给出了自由度分别为1、5和20的三种,2分布的概率密度曲线以及相应的累积分布 曲线。从图中可以看出,X分布的概率密度曲线不对称:∫越大,曲线越趋于对称。当∫→∞ 时,x2f)→NG,2 ①r国)=Hewp-0灿 ②k,a)=广户exp-)u. 风平是给喜些作药数尽管名为夫计的是正则化不充全鱼清藏。并丰不充全细清所以取名

.26 第2章分析化学中的误差和统计学处理 f-l 20 -2 随机变敏 30 40 随机变量 a 图2.4自由度不同的三种X分布的概率密度曲线(a)以及相应紫积分布曲线) 7.抽样分布之1分布 设总体X~N4σ),X,X,Xn是来自该总体的一个样本,那么以下形式的随机变量T 服从df为fU=n-1)的t分布,记作T~f)。 T=x-“ 式中,x表示样本均值s表示样本标准偏差 t分布的PDF为 p(x;f)- 14x2) 或者p(xf)= 式中,B表示贝塔函数beta function)2,可用Matlab库函数beta进行计算。 t分布的CDF为 P(x;f)= 2'f+222 1f. 2+x2'2 (x<0) 式中,I表示正则化不完全贝塔函数(regularized incomplete beta function),可用Matlab库函数 betaine进行计算. t分布CDF的Matlab计算程序可以参考附录1程序1.5。 ①:分布由英国统计学家W.S.Gosset在19O8年创立,发表论文的署名是Student,待名1分布,也称Student分布, ②B,)=∫r1-y,后文中F分布的PDF也用到贝塔函数 回低)-》,其中cx=r-y山为不完全现塔函数6 nmpe fuction.后文中F分布的cDF 也用到正则化不完全贝塔函数。该Maab库函数尽管名为betainc,.实际计算的是正则化不完全贝塔函数,并非不完全贝塔函数 所以取名betareg似乎更恰当一些
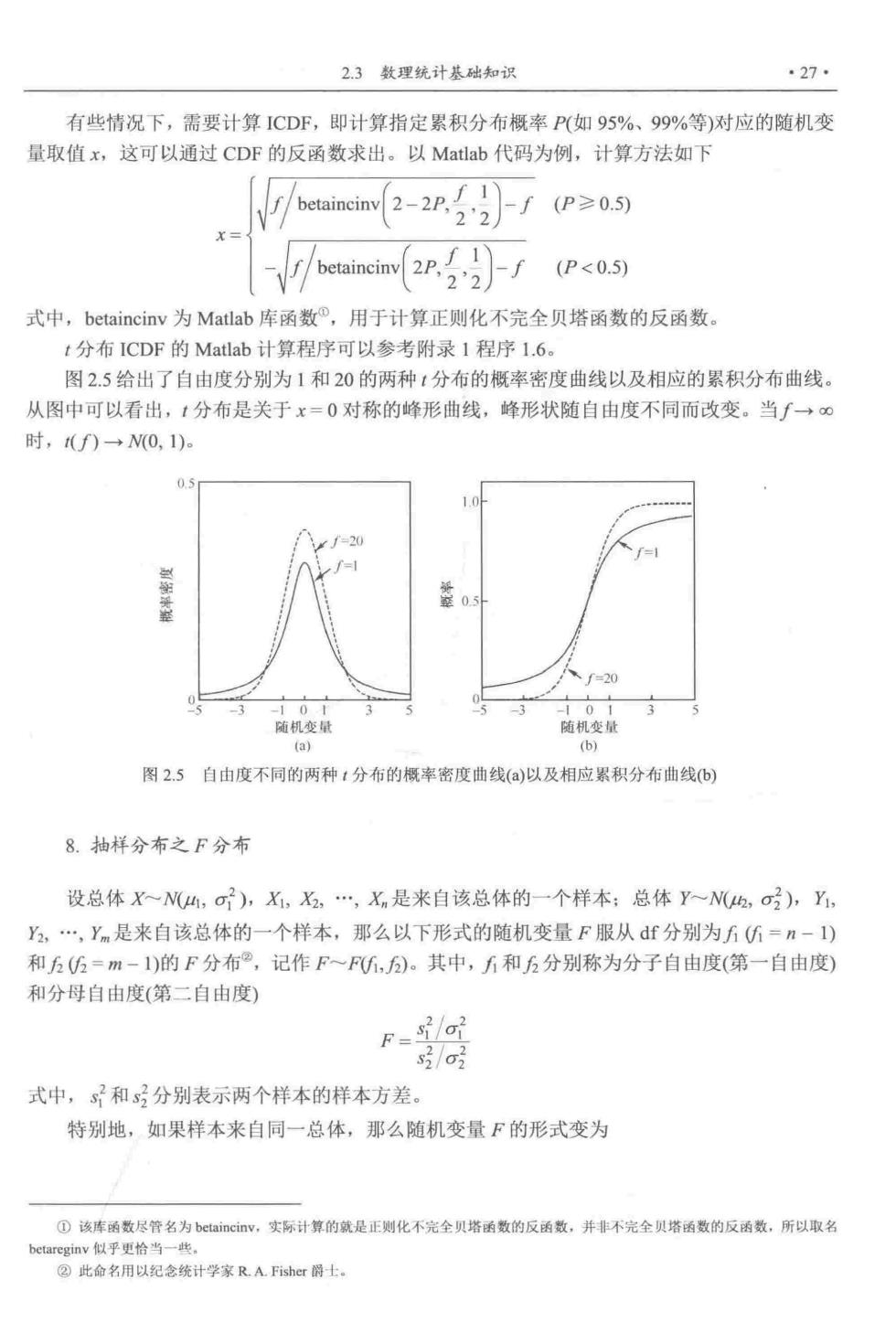
2.3数理统计基础知识 ·27 有些情况下,需要计算ICDF,即计算指定累积分布概率P(如95%、99%等)对应的随机变 量取值x,这可以通过CDF的反函数求出。以Matlab代码为例,计算方法如下 /(r.(03) 式中,betaincinv为Matlab库函数°,用于计算正则化不完全贝塔函数的反函数。 t分布ICDF的Matlab计算程序可以参考附录1程序1.6。 图2.5给出了自由度分别为1和20的两种1分布的概率密度曲线以及相应的累积分布曲线。 从图中可以看出,1分布是关于x=0对称的峰形曲线,峰形状随自由度不同而改变。当∫→© 时,f)→N0,1) 01 0 随机变量 变 图2.5自由度不同的两种1分布的橘率密度曲线()以及相应累积分布曲线b) 8.抽样分布之F分布 设总体XN山,2),X,X,Xn是来自该总体的一个样本:总体Y~Nh,o),Y, 2,.,ym是来自该总体的一个样本,那么以下形式的随机变量F服从f分别为6G=n-) 和五5=m-1)的F分布,记作F一F,分。其中,和五分别称为分子自由度(第一自由度) 和分母自由度(第二自由度) F= s/a 式中,和子分别表示两个样本的样本方差。 特别地,如果样本来自同一总体,那么随机变量F的形式变为 ①该库数尽管名为n,实标计算的是正测化不完全贝塔函数的反函数,并事不完全函数的反函数,所以取名 此名用以含计学家RA:士
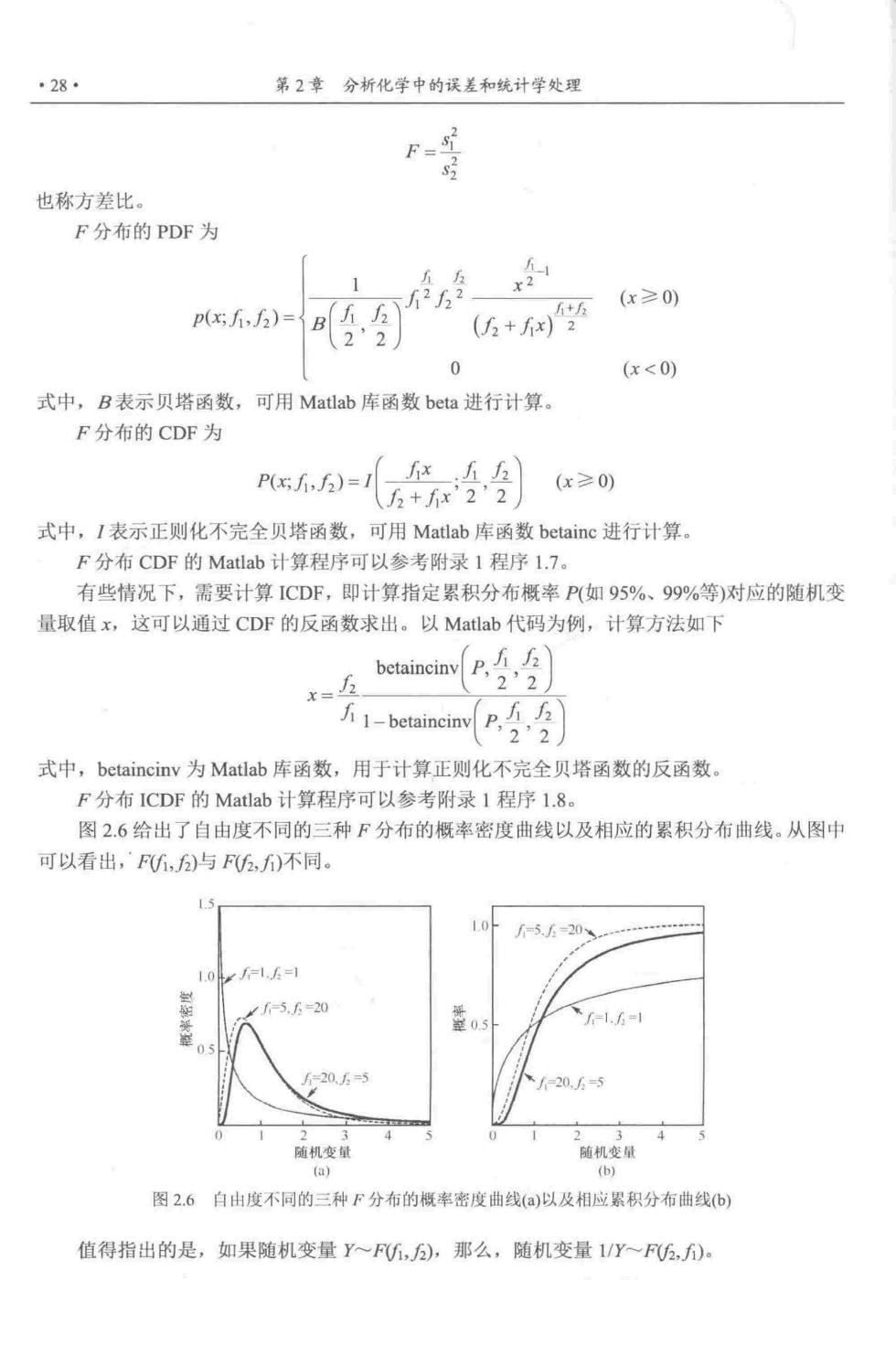
·28. 第2章分析化学中的误差和统计学处理 也称方差比。 F分布的PDF为 (x≥0) p(xh,f)= 2'2 (6+ 0 (x<0) 式中,B表示贝塔函数,可用Matlab库函数beta进行计算。 F分布的CDF为 P,月)=16+22 (x≥0) 式中,I表示正则化不完全贝塔函数,可用Matlab库函数betainc进行计算 F分布CDF的Matlab计算程序可以参考附录1程序L.7。 有些情况下,需要计算ICDF,即计算指定累积分布概率P(如95%、99%等)对应的随机变 量取值x,这可以通过CDF的反函数求出。以Matlab代码为例,计算方法如下 i1-betainciy,今,A 式中,betaincinv为Matlab库函数,用于计算正则化不完全贝塔函数的反函数。 F分布ICDF的Matlab计算程序可以参考附录1程序l.8。 图2.6给出了自由度不同的三种F分布的概率密度曲线以及相应的累积分布曲线。从图中 可以看出,'F,)与F5,)不同。 101,1 f=5.6=20 206= 4 随机变量 随机变量 图2.6白由度不同的三种F分布的概率密度曲线()以及相应累积分布曲线b) 值得指出的是,如果随机变量Y~F,),那么,随机变量1/Y~F5,)