
2.3数理统计基础知识 ·29. 2.3.3显著性检验 1.关于显著性检验 在误差分析中引入数理统计的主要目的是,判断误差是否源自随机因素。这一问题可以通 过显著性检验(test of statistical significance)来解决。显著性检验属于数理统计中的“假设检验”。 关于假设检验的简单介绍参见附录2。 如果误差在统计意义上不显著(statistically insignificant),说明该误差源自随机因素,那么 坦然接受这一现实。如果误差在统计意义上显著(statistically significant),说明该误差源自非随 机因素,即确定性因素,而确定性因素是人力可为的,那么,可以进一步探究测量系统是否存 在缺陷或者相关理论是否仍需完善 显著性检验基于一个常识:有些事件的发生属于“异常”,引人注意:另外一些事件的发 生属于“正常”,司空见惯。所谓“异常”或者“正常”,是指实际结果与我们的预想不同或 者相同。一个“异常”事件的发生有两种情形:一种是“异常”事件确实发生了,尽管经验表 明,这种可能性很小:而另一种情形更有可能,那就是预想并不正确。因此,通过对所发生 事件进行“异常”或者“正常”的归属,就可以判断预想是否合理。日常生活中,我们会对“异 常”和“正常”事件的范围做出大致划分,而划分的依据是经验:通常经验越丰富,结论越 靠 以上述事实作类比,显著性检验就比较容易理解了。事件在显著性检验中用一个随机变量 来表征,称为检验统计量(test statistic))。“异常”事件的发生相当于检验统计量的取值落入小 概率区间:“正常”事件的发生相当于检验统计量的取值落入大概率区间。“预想”相当于原 假设(null hypothesis),显著性检验的原假设是:事件的发生源自随机因素。无限丰富的经验相 当于检验统计量的分布。“异常”和“正常”事件发生范围的划分相当于基于检验统计量的分 布,确定小概率区间和大概率区间。 在显著性检验中,首先根据具体检验问题,选择合适的检验统计量,然后计算检验统计量 在该问题中的取值,进行判断:如果该取值落入了小概率事件发生范围,说明事件的发生很可 能并不源自随机因素,那么拒绝原假设,从而得出结论:“统计意义上显著”;如果该取值落 入了大概率事件发生范围,说明事件的发生很可能源自随机因素,那么接受原假设,从而得出 结论:“统计意义上不显著”。 上述“大概率”和“小概率”对应于显著性检验中的两个概念,分别是“置信度”(confidence) 和“显著性水平”(significant level,二者之和为1。显著性水平以a表示, 一般设定为5%或 者1%。 然而,小概率事件还是有可能发生的,尽管可能性很小,这种情况下,拒绝了实为正确的 次试验 者事先确定。原假设当 理由绝假设(相当于文中的“预想并不正确”)】 ②在假设检验中,小概率事件发生的范围称为拒绝域(心ject,)大概率事件发生的范围称为接受域(acceptance region)。 检验统计量的削取值如果落入拒绝域则拒绝原假设,如果落入接受域则接受原假设

30. 第2章分析化学中的误差和统计学处理 原假设,“统计意义上显著”这一结论就是错误的,犯这种错误的概率等于显著性水平α。另 外,大概率事件也可能不发生,尽管这个可能性也很小,这种情况下,接受了实为错误的原假 设,“统计意义上不显著”这一结论也是错误的,犯这种错误的概率以B表示,B一般无法得 到,因为通常缺少此信息:原假设为假时检验统计量的分布。 上述问题实际上是假设检验中的第一类错误一“弃真”错误(原假设为真却拒绝了原假 设)和第二类错误一“存伪”错误(原假设为假却接受了原假设)。不可能同时减小α和B,减 小犯一类错误的概率就会增大犯另一类错误的概率。在显著性检验中,需要控制犯第一类错误 的概率,a一毁取0.05或者0.01。有兴趣的读者可可以进一步阅读附录2。 综上所述,如果结论是“统计意义上显著”,那么该结论正确的概率等于1一,也可以说 该结论的可靠性为1一α,还可以说该结论错误的概率等于α。然而,如果结论是“统计意义上 不显著”,那么该结论正确的概率一般不可知。 显著性检验的要素是显著性水平、检验统计量以及原假设成立时检验统计量的分布。 2.显著性水平 显著性水平α设置得越大,“统计意义上显著”这一结论的可靠性越低,然而好处是,提 高了另一结论“统计意义上不显著”的可靠性(B变小)。显著性水平α设置得越小,“统计意 义上显著”这一结论的可靠性越高,然而坏处是,降低了另一结论“统计意义上不显著”的可 靠性(B变大) 下面的例子有助于更好地理解上述内容。 假设某地区成年男子的身高近似服从平均值为1.72m的正态分布。现在根据这个分布来 判断“某人是否明显是高个儿”。图2.7()中,:设置得过大(大片阴影),相应的临界值为 1.75m,这种情况下,身高略超过1.75m的人就会被认为“明显是高个儿”,该结论不甚可 靠:但是,身高低于1.75m的人“不能认为是明显高个儿”,这个结论就可靠多了。图2.7b) 中,α设置得过小(阴影勉强可见),相应的临界值为1.91m,这种情况下,身高超过1.91m的 人会被认为“明显是高个儿”,该结论相当可靠;但是,对于身高略低于1.91m的人,却“不 能认为是明显高个儿”,显然不太合常理。 身高 身高 图2.7以某地区成年男子的身高分布为例,图解显著性水平a过高()和过低(b)的情形 图中阴影部分的面积等于
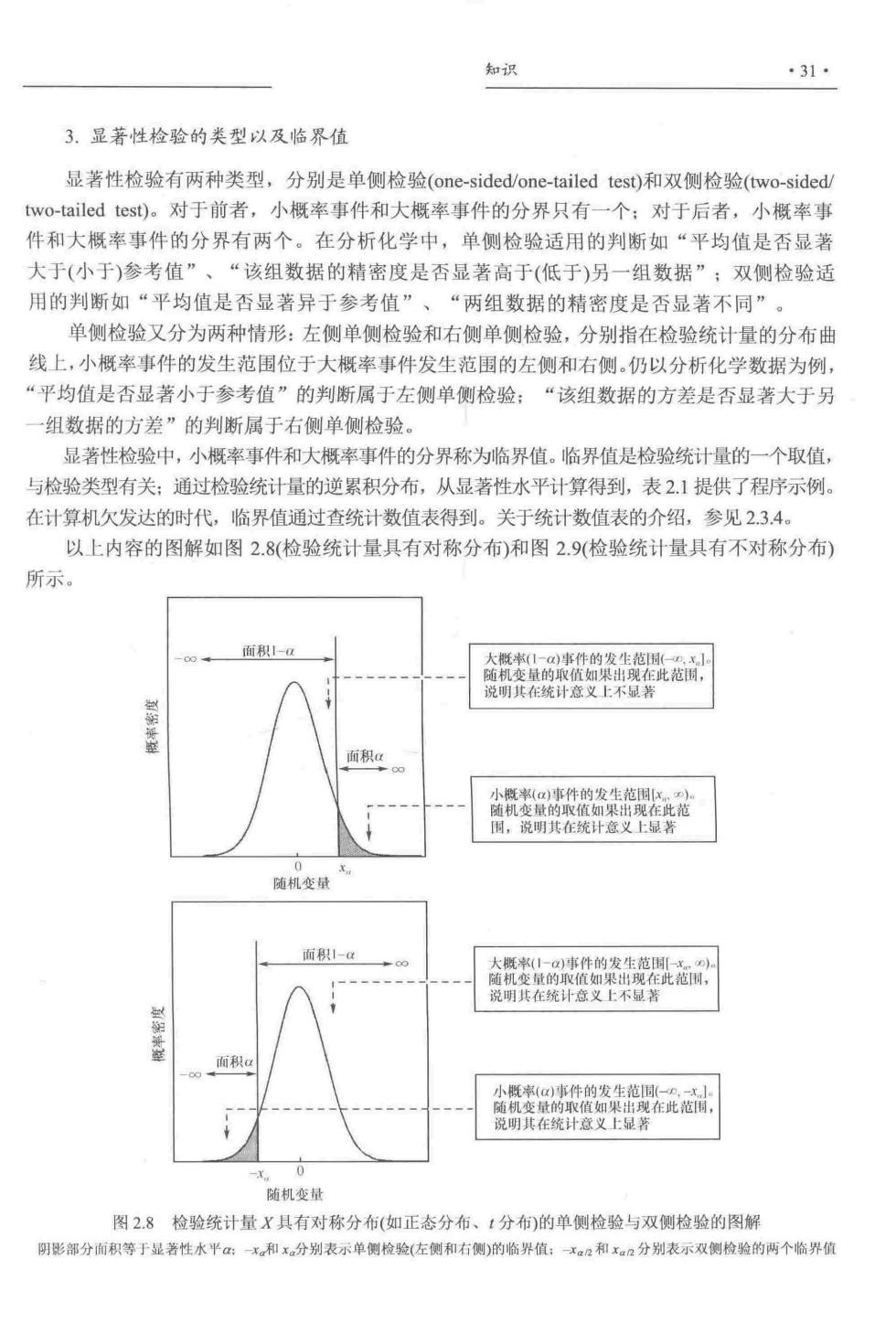
知识 ·31· 3.显著性检验的类型以及临界值 显著性检验有两种类型,分别是单侧检验(one-sided/one-tailed test)和双侧检验(two-sided/ two-tailed test)。对于前者,小概率事件和大概率事件的分界只有一个:对于后者,小概率事 件和大概率事件的分界有两个。在分析化学中,单侧检验适用的判新如“平均值是否显著 大于(小于)参考值”、“该组数据的精密度是否显著高于(低于)另一组数据”;双侧检验适 用的判断如“平均值是否显著异于参考值”、“两组数据的精密度是否显著不同”。 单侧检验又分为两种情形:左侧单侧检验和右侧单侧检验,分别指在检验统计量的分布曲 线上,小概率事件的发生范围位于大概率事件发生范围的左侧和右侧.仍以分析化学数据为例, “平均值是否显著小于参考值”的判断属于左侧单侧检验:“该组数据的方差是否显著大于另 ~组数据的方差”的判断属于右侧单侧检验。 显著性检验中,小概率事件和大概率事件的分界称为临界值。临界值是检验统十量的一个取值, 与检验类型有关:通过检验统计量的逆累积分布,从显著性水平计算得到,表2.1提供了程序示例 在计算机欠发达的时代,临界值通过查统计数值表得到。关于统计数值表的介绍,参见23.4。 以上内容的图解如图2.8(检验统计量具有对称分布)和图2.9(检验统计量具有不对称分布) 所示。 面积1 说明其在统计意义上不显著 面积 国,说明其 随机变量 纯义上不显若 面积 牛的发生礼 正在统义显 随机变量 图2.8检验统计量X具有对称分布(如正态分布、t分布)的单侧检验与双侧检验的图解 明影部分面积等于显著性水平:和x分别表示单侧检验(左侧和右侧)的临界值:X和。2分别表示双侧检验的两个临界

·32 第2章分析化学中的误差和统计学处理 L面积1- 说明其在统计意义上不显芳 小概(a事件的发生范( 随机变 图2.8(续) 面积1-a 说明其在统计意义上不显 面积 围,说明其在统计意义上显 随机变星 面积1-位 说明其在统意义上不显 说明其在统计意义上显 随机变量 图2.9检验统计量X具有不对称分布(如/分布、F分布们的单侧检验与双侧检验的图解 阴影部分面积等于显著性水平:和和x分别表示单侧检羚(左侧和右侧的临界值:和分别表示双侧检验的两个界值

2.3数理统计基础知识 ·33· 面积1一 明其在统计义上不显若 面积a。 概事件的发生 在此国,说明其在统计意义证 随机变量 图2.9(续) 表2.1列出了一些常见分布的临界值的符号表示,以及如何使用附录1中的Matlab程序 进行计算。子分布和F分布的临界值符号表示稍显复杂,第一个脚标在数值上等于1'-CDF, 只要清楚CDF的定义(2.3.2第二部分),再结合图2.8和图2.9,不难理解。 表2.1显著性检验中临界值的符号表示以及计算(显著性水平为 分布类型 检验类型 临界值的符号表示 临界值计算) 左侧单侧检验 cdfnorm(a0.1 MO,1)分布 右侧单侧检验 a cdfnorm(1-a.1) 双侧检验 -g/2,Mg/2 cdfnorm(a/2.0,1) cdinorm(I/2.0.1) 左侧单侧检验 icdfchi2(a.) 分布 右侧单侧检验 iedfchi2(1af) 双侧检验 icdfchi2(a/2. iedfchi2(/2. 左侧单侧检验 -ta:I iedft(a.f) 1分布 单侧检验右侧 icdn(a) 双侧检验 -lal2flar2/ a2a2n 左侧单侧检验 F。方 F分布 右侧单侧检验 Fa.h.Ia icdffI-af6) 双侧检验 月e2ih,2ih icdffla/2.6) icdff(1-a/2.f) )使用附录中的Maab程序。 F分布的临界值有一个重要性质:R。人5=1/R。65(注意分子自由度和分母自由度发生 了互换)。该性质可以用于从F分布数值表获取R。,(6(左侧单侧检验的临界值),因为表中的 临界值都是。5(佑侧单侧检验的临界值):欲得到。6,需从表中查到E。6,然后取 倒数