
2.3数理统计基础知识 ·19· 思维活动的系统化。数理统计方法的学习难点不在于其中的数学知识,而是观点和思想。读者 如果觉得本节涉及的数理统计概念或者原理过于抽象,可以试着沿用先贤们的归纳法,结合具 体事件来理解。 数理统计应用中的计算不是重点,更不应该是障碍,所以本节涉及了一些Maab应用,目 的是借助计算机快速完成数值运算。本节包含了一些必要公式,一方面是出于数理统计知识完 整性的考虑,另一方面也是为了方便Matlab编程(相关程序附于书后供参考): 2.3.1在误差分析中应用数理统计方法的必要性 分析化学中,数据处理不仅是数值计算,还应该分析随机因素和确定性因素对结果的影响, 做出合理的判断以及更高级别的解释,尽量发掘测量数据中的显性和隐性信息。为了实现这些 目的,需要采用数理统计方法对结果进行误差分析。 误差分析的必要性容易理解,但是为什么要采用数理统计方法呢?根本原因(尽管看起来 不那么直接)在于人类认识世界和改造世界的能力:强大却有限。人们在自然科学研究中,显 然应该将有限的力量放在能够充分发挥其作用的地方,而数理统计方法可以帮助确定这种着力 之处 如果导致误差的原因是确定性的,如测量仪器精度不够,实验方案不完善,这时人们就有 了可以着力之处,如改进仪器、完善方案,甚至暂缓研究,都是可选项。 如果导致误差的原因是非确定性的、随机的,那么这种情况下人们可“做”的事就比较简 单一接受。不确定性是自然界的特征之一,人类无法预知也不可控制(在人类施力范围之外), 因此没有必要过多关注。 要言之,在科学研究中,对于确定性因素,我们很感兴趣:对于随机因素,我们坦然接 受。那么如何区分确定性因素和非确定性因素?答案是通过数理统计方法。 研究随机因素的基础知识是随机变量和统计规律性,下面具体介绍。 2.3.2随机变量及其分布 由于不确定性,随机误差对单次测量结果的影响无法预知,当然也就无从研究。然而在相 同条件下进行多次测量,这些测量结果可以显示出随机误差的统计规律性。之所以强调相同条 件下的测量,目的是固定可能存在的系统误差,以消除其对随机误差分布的影响。 上述随机误差以及随机误差的统计规律性是数理统计中两个基本概念的具体化。这两个概 念是随机变量和随机变量的分布(distribution)。随机变量可以视为取值随机,而在确定范围内 ①范例:瑞利助爵Lord Raylig发现,从化学反应制备出的每升质量为1205g,而从空气中分离出的每升质量为1252g(除 去 又编某分折化学 分析误差减小的原因。如果确是由 是冷静地通过数理统计方法 也料庆祝。然面,如果误差的小极有可能是随机因素造成的,郑么没必要这些事了,因为机 误差减小只是巧合。值得指出的是,后一种情况也不是令人温丧的。新方案在准确度上没有显示出优越性,但同时也说明准确度没 有降低一这他是数理统计的一种结论。如果新方案具备其他优点,如测量时间短、成本低等,那么新方案值得肯定一现在可以 庆祝了
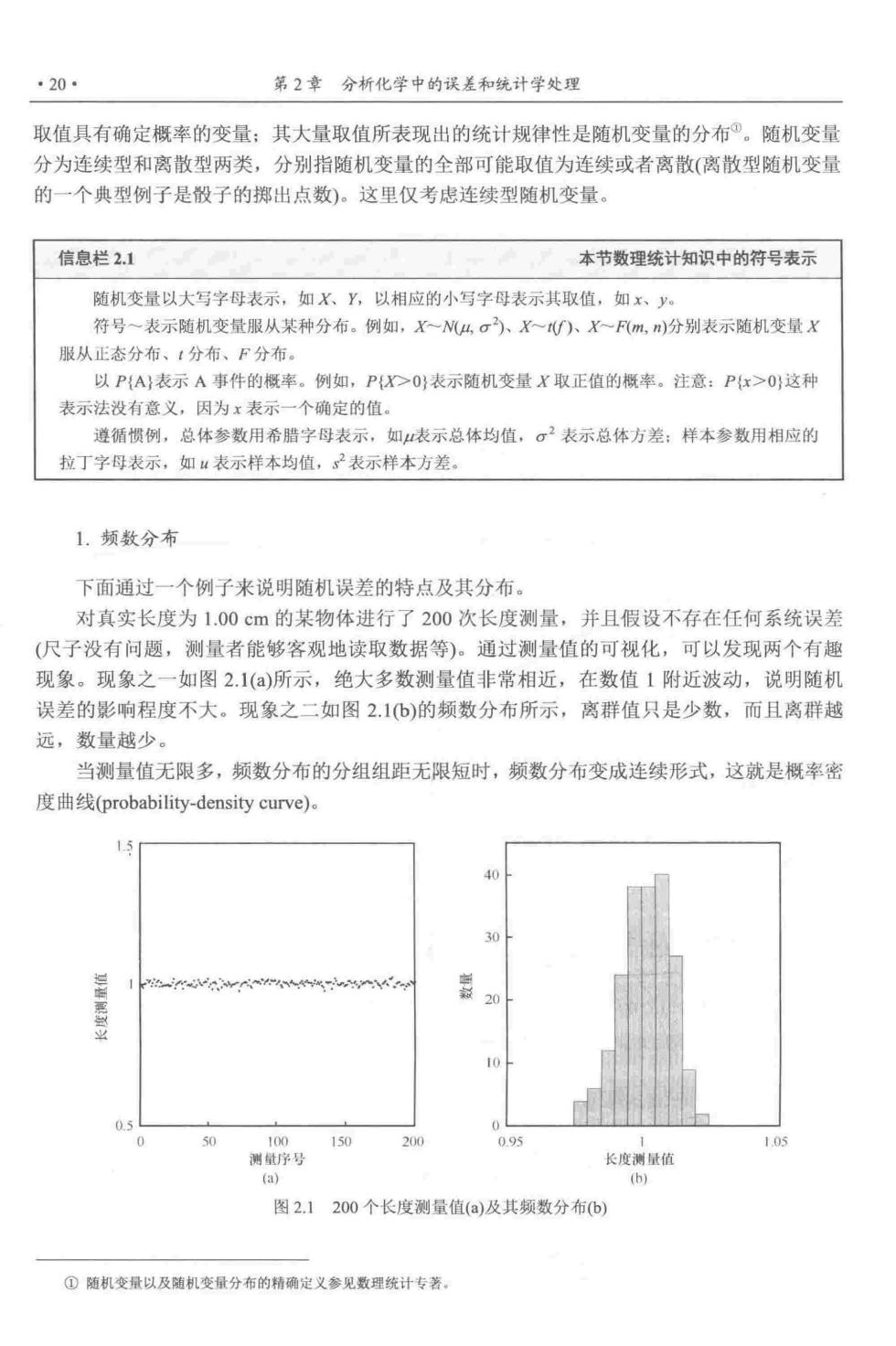
·20- 第2章分析化学中的误差和统计学处理 取值具有确定概率的变量:其大量取值所表现出的统计规律性是随机变量的分布。随机变量 分为连续型和离散型两类,分别指随机变量的全部可能取值为连续或者离散(离散型随机变量 的一个典型例子是骰子的掷出点数)。这里仅考虑连续型随机变量。 信息栏2.1 本节数理统计知识中的符号表示 随机变量以大写字母表示,如X、Y,以相应的小写字母表示其取值,如x、y。 符号一表示随机变量服从某种分布。例如,XMσ)、X)X一F风m,)分别表示随机变量X 服从正态分布、‘分布、F分布。 以P{A}表示A事件的概率。例如,PX>O}表示随机变量X取正值的概率。注意:P红>0;这种 表示法没有意义,因为x表示一个确定的值。 遵循惯例,总体参数用希腊字母表示,如表示总体均值,σ2表示总体方差;样本参数用相应的 拉丁字母表示,如“表示样本均值,2表示样本方差。 1.频数分布 下面通过一个例子来说明随机误差的特点及其分布。 对真实长度为1.00cm的某物体进行了200次长度测量,并且假设不存在任何系统误差 (尺子没有问题,测量者能够客观地读取数据等)。通过测量值的可视化,可以发现两个有趣 现象。现象之一如图2.1()所示,绝大多数测量值非常相近,在数值1附近波动,说明随机 误差的影响程度不大。现象之二如图2.1b)的频数分布所示,离群值只是少数,而且离群越 远,数量越少。 当测量值无限多,颜数分布的分组组距无限短时,频数分布变成连续形式,这就是概率密 度曲线(probability-density curve). -wrw%w 50 150 200 095 长酒 图2.1200个长度测量值(a)及其频数分布b) ①随机变量以及随机变量分布的精确定义参见数理统计专著
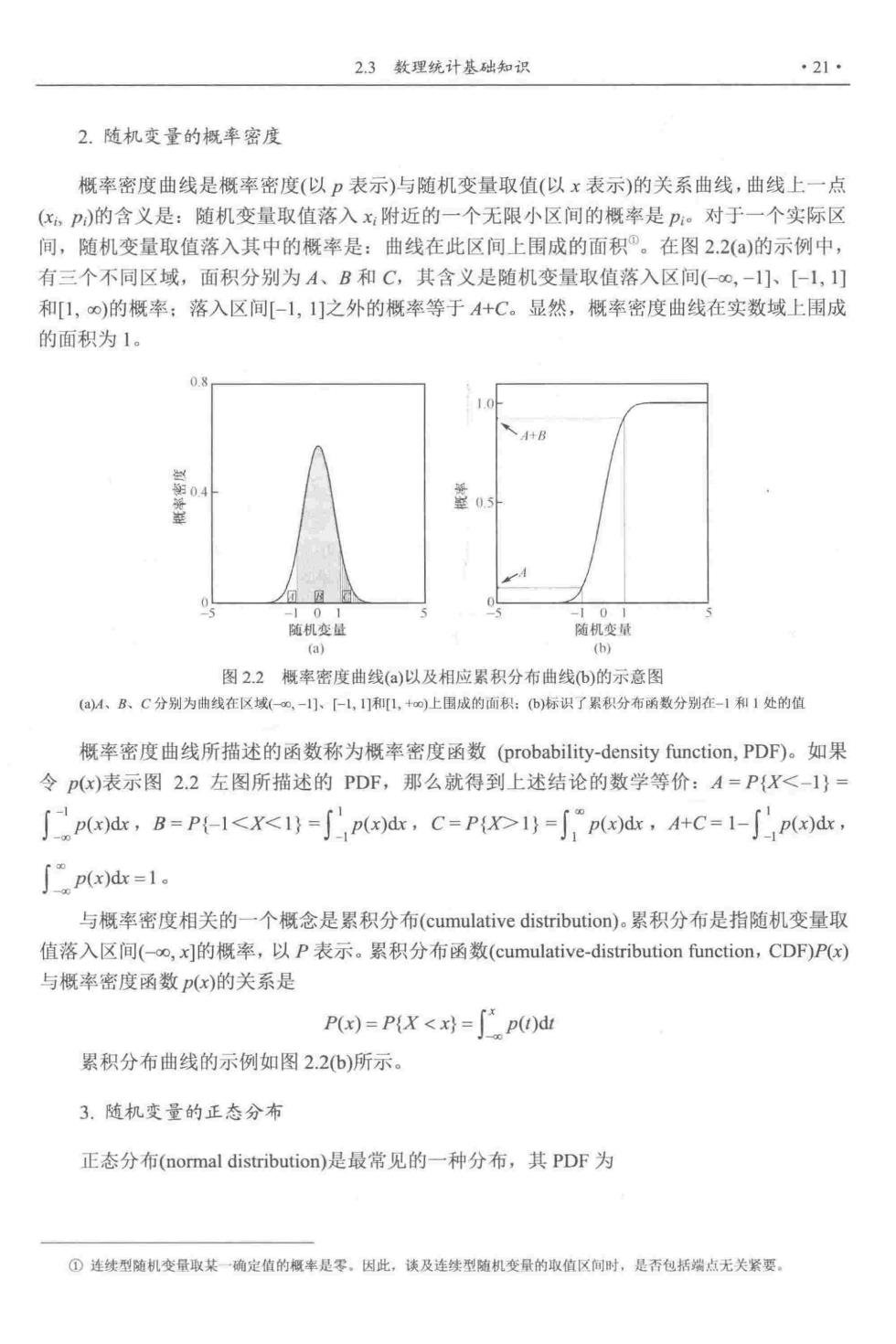
23数理统计基础知识 ·21· 2.随机变量的概率密度 概率密度曲线是概率密度(以p表示)与随机变量取值(以x表示)的关系曲线,曲线上一点 (x,P)的含义是:随机变量取值落入x附近的一个无限小区间的概率是P。对于一个实际区 间,随机变量取值落入其中的概率是:曲线在此区间上围成的面积°。在图2.2()的示例中, 有三个不同区域,面积分别为A、B和C,其含义是随机变量取值落入区间(-0,-1]、[-1,1] 和[1,∞)的概率;落入区间[-1,1]之外的概率等于4+C。显然,概率密度曲线在实数域上围成 的面积为1。 、B 随机变量 随机变量 (a) h 图22概案密度曲线(a)以及相应累积分布曲线)的示意图 (4、B、C分别为曲线在区域(一,-小、【L,和1,+)上国成的面积:b)标识了累积分布函数分别在-和1处的位 概率密度曲线所描述的函数称为概率密度函数(probability-density function,PDF)。如果 令p()表示图2.2左图所描述的PDF,那么就得到上述结论的数学等价:A=PX<-1} Jp(edc,B=P-1<X<1y=∫Pxt,C=P1y=∫pdr,A+C=1-∫pd, px=1。 与概率密度相关的一个概念是累积分布(cumulative distribution).累积分布是指随机变量取 值落入区间(-oo,xj的概率,以P表示。累积分布函数(cumulative-distribution function,CDF)P(x) 与概率密度函数px)的关系是 Px)=PX<x对=p)d 累积分布曲线的示例如图2.2(b)所示。 3.随机变量的正态分布 正态分布(normal distribution)是最常见的一种分布,其PDF为 ①连续型随机变量取某一确定值的概丰是零。因此,谈及连线型随机变量的取值区间时,是香包括端点无关紧要

·22 第2章分析化学中的误差和统计学处理 1 (x-}2 p=2c22 (2.10 式中,μ和σ分别表示随机变量X的数学期望(总体平均值)和方差,是正态分布的两个参数。 正态分布以N(4σ)表示。 正态分布的CDF为 (2.2) 气2 式中,erft表示互补误差函数(complementary error function)P,可用Matlab库函数erfc进行计算 正态分布CDF的Matlab计算程序可以参考附录1程序l.1。 有些情况下,需要计算逆累积分布(inverse cumulative distribution function,ICDF),即计算 指定累积分布概率P(如95%、99%等)对应的随机变量取值x,计算方法如下 x=a-g√2 erfcinv(2P) 式中,erfcinv表示互补误差函数的反函数,可用Matlab库函数erfcinv进行计算。 正态分布ICDF的Matlab计算程序可以参考附录1程序1.2。 图23给出了N(0,0.25)和N0,1)两个正态分布的概率密度曲线以及相应的累积分布曲 线。从图中可以看出,正态分布是关于x=4对称的峰形曲线:峰位置由μ控制,峰宽由σ控 制,σ≈0.5Wa6(Wa6表示0.6倍峰高处的峰宽): 0= y0c-02 0 0= 0.a-02 39 图2.3参数不同的两个正态分布的概率密度曲线()以及相应累积分布曲线(b) N0,1)称为标准正态分布。通过一些简单数学变换,标准正态分布可以与任意参数的正态 分布相互转换,这一性质使得相关计算更加便捷,下面是具体说明。 以p)和px)分别表示NO,1)和N4o的PDF,那么存在以下关系 =二,p)=op) 通过以上简单变换,从标准正态分布的概率密度可以方便地获得任意参数正态分布的概率 erfe(x)="exp(-ydr

2.3数理统计基础知识 ·23 密度。例如,Matlab函数randn生成服从NO,1)分布的随机数,通过命令g*randn+u即可得 到服从N(4σ)分布的随机数。再如,从N(0,1)概率密度曲线的坐标(4,),可以便捷地得到 N(4σ概率密度曲线的坐标,为(σ*u+丛,这样,基于已知的标准正态分布曲线,以相 当简单的运算就能够绘制任意参数正态分布曲线,而不必通过(2)式重新计算坐标。 以P(u和P(x)分别表示NO,I)和N(4d)的CDF,那么存在以下关系 u=x-4,P(u)=P(x) 在计算工具欠发达的年代,使用(2.2)式计算N(4σ)的累积分布概率是一件很困难的事。为 了解决这一难题,人们制作了NO,1)的累积分布概率数值表,即不同u值与其对应的P()。通 过这种数值表和上述简单变换,无需计算工具即可得到任意参数正态分布(4,的累积分布 概率。关于标准正态分布统计数值表,参见2.3.4。 下面是两个关于正态分布的实例 例2.4 正态分布:低难度 机变量X~一N(20.2),求X的取值落入「16.221的概率 解通过累积分布概率求得X落入[16,22]的概 P=P(16<X<22)=CDF-2-CDF-16 使用附录1程序1.1,输入如下语句即可得到结果0.9190。 cdfnorm(22.20,sqrt(2))-cdfnorm(16,20,sqrt(2)) 例2.5 正态分布;中等难度 分析仪器在没有样品时的连续输出称为基线。某仪器开机预热一段时间后基线平稳,设基线数据服 从正态分布N(0,0.01),计算基线数据中出现大于0.3的值的概率。 解根据题意,所求概率的计算式如下 P=PX>0.3}=1-CDFk-03 使用附录1程序1.1,输入如下语句即可得到结果0.0013。 1-cdfnorm(0.3.0.0.1) 本例说明,纯噪声中出现明显偏大的数值的可能性很小(概率仅为0.13%)。如果仪器输出了较大的数 值,那么可能是发生了小概率事件,然而更有可能是出现了非随机信感一分析信号。这是确定分析仪器 检测限的统计学基础,详细讨论参见24.1 正态分布极为常见,尤其当观测数据很多时,表现出的规律性与正态分布相当吻合。但是, 在数据量较小的场合,实际情况与正态分布有一定偏离。因此,有必要研究少量数据的分布, 这是抽样分布要解决的问题。 4.抽样分布 在很多分析实例中,一个司空见惯然而逻辑上不甚严密的做法是,将样品的分析结果推厂 到整体。例如,通过测定化学耗氧量来了解某湖泊的污染情况:取一些水样进行分析,最后的 结论却是“该湖泊的污染情况如何.”。尽管很多结论(至少在逻辑上)应该从全部研究对象