第十一章压杆稳定问题 引言 M=一Fw EIw”=M=-Fw w=0k2= F El w2+k2w=0 通解w=A sinkx+B coskx 边界条件i.x=0,w=0 B=0 w=A sinkx ⊙嘉道人善
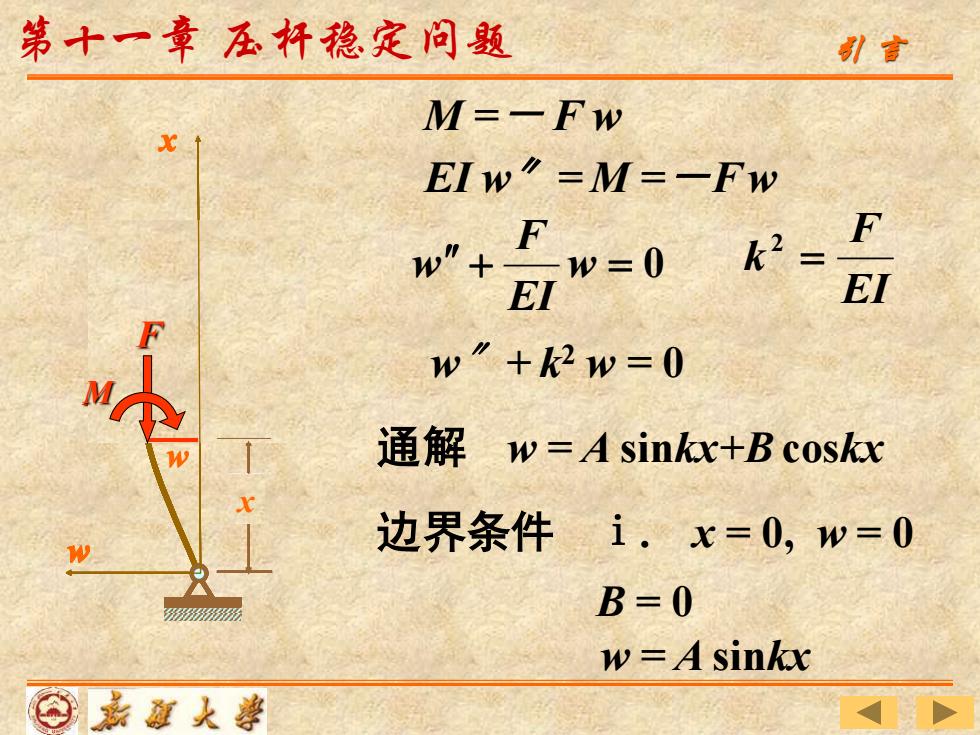
w x w F M x F w F M x w F M w = A sinkx B = 0 边界条件 ⅰ. x = 0, w = 0 通解 w = A sinkx+B coskx w 〞+ k2 w = 0 EI F k = 2 M =- F w EI w〞= M =-F w + w = 0 EI F w 第十一章 压杆稳定问题 引 言
第十一章在杆稳定问题 引言 w=A sinkx 边界条件ii.x=l,w=0 A sinkl=0A≠0 sinkl =0 kl=nπ n=1,2,. n2π2EI 形 取n=1r- 欧拉公式 ⊙嘉道大事
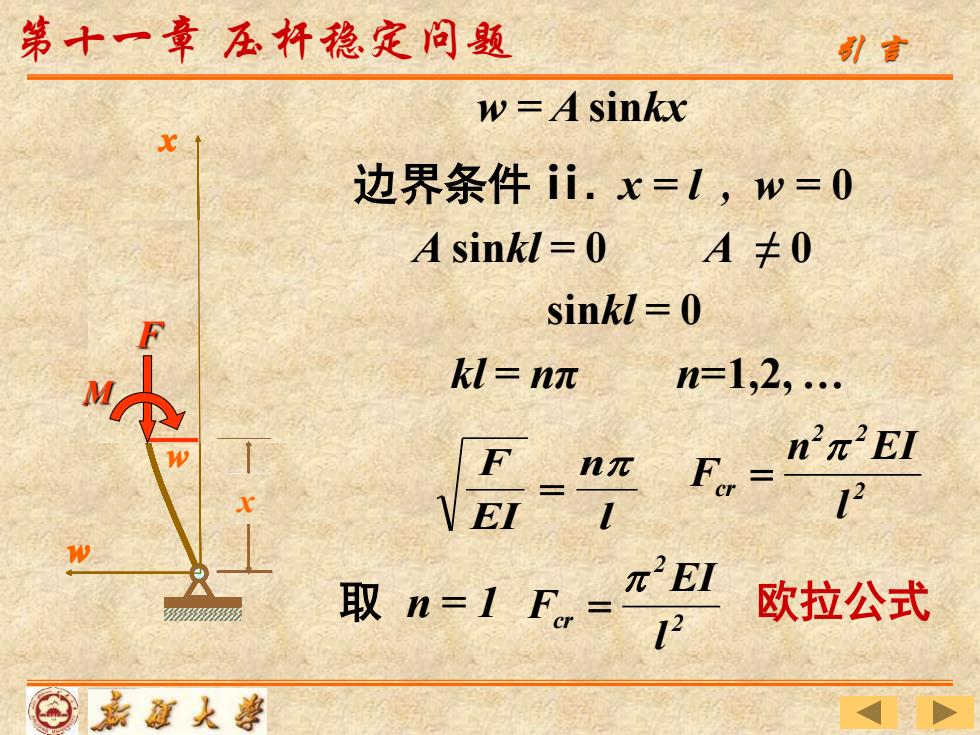
w x w F M x F w F M x w F M 欧拉公式 2 2 2 cr l n EI F = l n EI F = 边界条件 ⅱ. x = l , w = 0 A sinkl = 0 A ≠ 0 sinkl = 0 kl = nπ n=1,2, . w = A sinkx 引 言 取 n = 1 2 2 cr l EI F = 第十一章 压杆稳定问题

第十一章压杆稳定问题 引言 两个结果 临界力公式 π2EI 12 弯曲曲线公式 w=Asinkx w=4s 半波正弦曲线 ⊙嘉道人導
两个结果 临界力公式 2 2 l EI Fcr = 弯曲曲线公式 w = Asinkxx l w A = sin 半波正弦曲线 第十一章 压杆稳定问题 引 言

第十一章压杆稳定问题 雨感腺食式脚仪丞并的修界戒局 §11-3 两端非铰支细长压杆的临界载荷 方法1:同欧拉公式, 微分方程+边界条件 方法2:相当长度法 在压杆中找出长度相当于两端铰支 的一段(即两端曲率为零或弯矩为零), 该段失稳曲线为半波正弦曲线,该段临 界力即压杆的临界力。 ⊙嘉人尊
方法1: 同欧拉公式, 微分方程 + 边界条件 方法2: 相当长度法 在压杆中找出长度相当于两端铰支 的一段(即两端曲率为零或弯矩为零), 该段失稳曲线为半波正弦曲线,该段临 界力即压杆的临界力。 §11-3 两端非铰支细长压杆的临界载荷 第十一章 压杆稳定问题 两端非铰支细长压杆的临界载荷
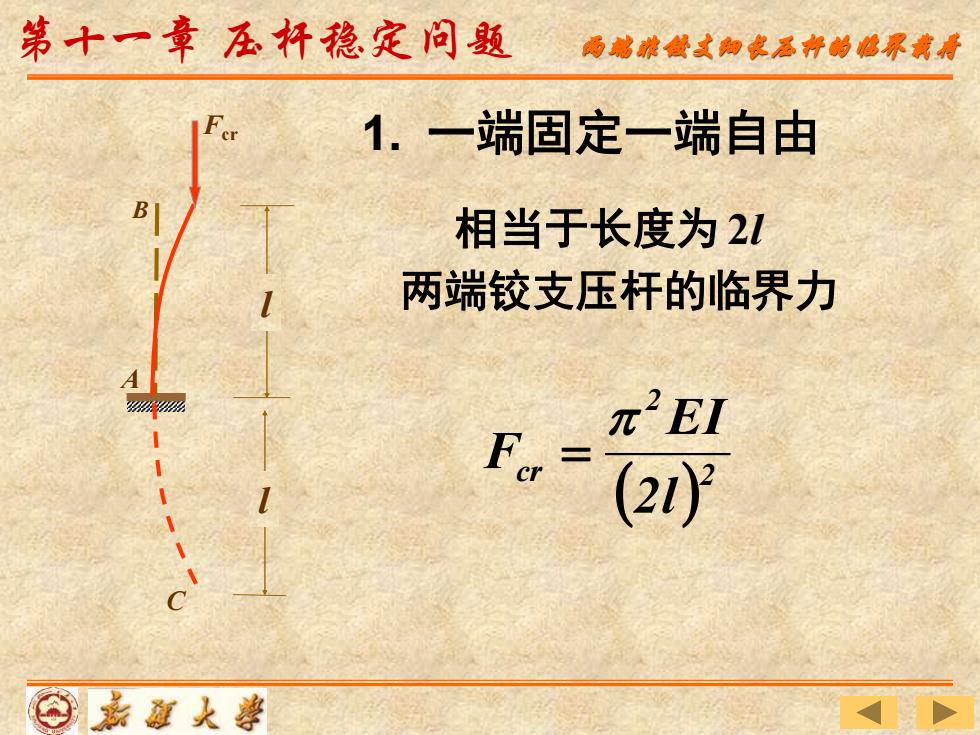
第十一章在杆稳定问题 雨感琥藏式脚总层特的感尿戒青 1.一端固定一端自由 相当于长度为2L 两端铰支压杆的临界力 π2EI -70 (2}
l A B 1. 一端固定一端自由 ( ) 2 2 cr 2l EI F = Fcr l C 相当于长度为 2l 两端铰支压杆的临界力 第十一章 压杆稳定问题 两端非铰支细长压杆的临界载荷