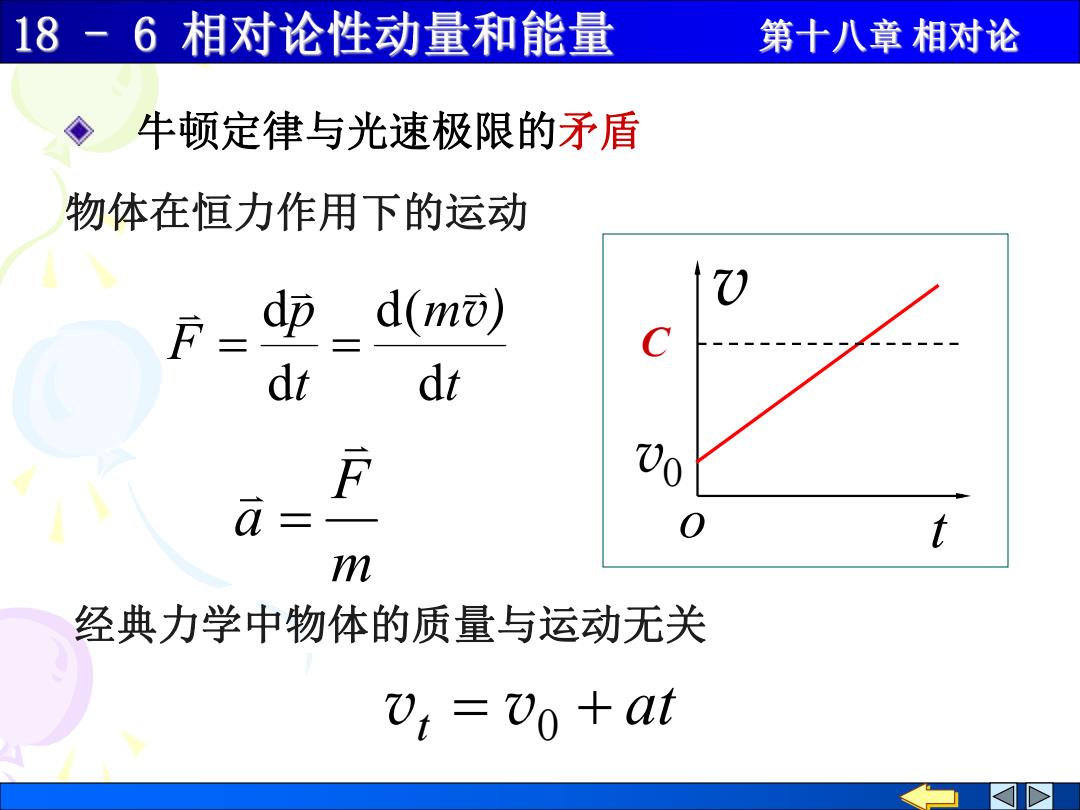
18-6相对论性动量和能量 第十八章相对论 牛顿定律与光速极限的矛盾 物体在恒力作用下的运动 d啦 d(mò) dt dr F 00 a t m 经典力学中物体的质量与运动无关 V:=70 +at
牛顿定律与光速极限的矛盾 t m t p F d d( d d v) m F a t v C 0 v o 物体在恒力作用下的运动 at vt v0 经典力学中物体的质量与运动无关
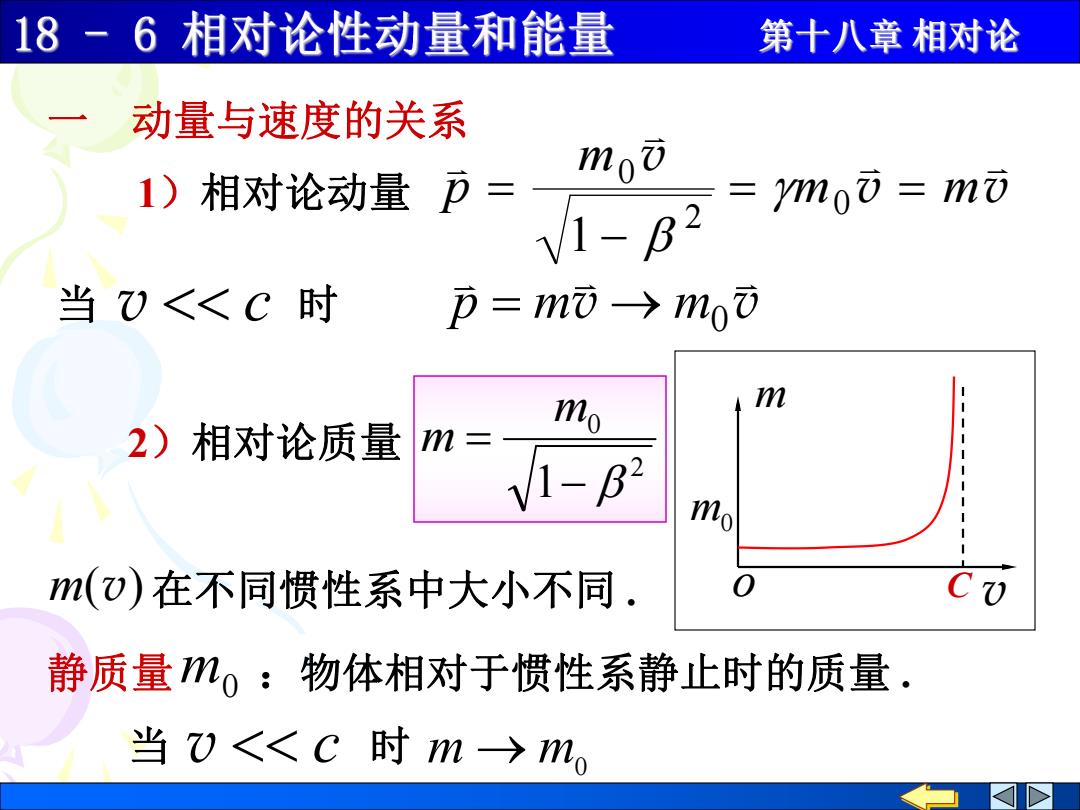
18 -6相对论性动量和能量 第十八章相对论 动量与速度的关系 mo 1)相对论动量p= V1-B2 =0i=m元 当)<<C时 p=mō→mo m 1 2)相对论质量 mo m= V1-B2 1 mo m(o)在不同惯性系中大小不同. 静质量mo:物体相对于惯性系静止时的质量. 当)<<C时m→mo
1)相对论动量 v v v m m m p 0 2 0 1 当 v c 时 v v m m0 p 一 动量与速度的关系 2)相对论质量 2 0 1 m m 静质量m0 :物体相对于惯性系静止时的质量 . m(v) 在不同惯性系中大小不同 . 当 v c 时 m m0 v m C m0 o

18-6相对论性动量和能量 第十八章相对论 狭义相对论力学的基本方程 òdx mo dō dm V1-B21 =m dt dr dt ò 当 )<<C时 m→1mo =m dr 当)>c时,dm/dt急剧增加,而a>0 所以光速C为物体的极限速度, 相对论动量守恒定律 当 ∑F=0时,∑p,=∑ mi0⑦i 不变. i 1-B2
二 狭义相对论力学的基本方程 ) 1 ( d d d d 2 0 v m t t p F 相对论动量守恒定律 t m t m d d d d v v 当 时, 急剧增加 , 而 , 所以光速 C 为物体的极限速度. v c dm dt a 0 i i i i i i i m F p 2 0 1 0 v 当 时, 不变 . t c m m F m d d 0 v v 当 时

18-6相对论性动量和能量 第十八章相对论 三 质量与能量的关系 动能定理△Ek-∫F.dr-mv2- 2 设 Eko=0F=Fi 0=0 dx dudg mv 利用 d(pw)=pdo+wdp和p= V1-B2 得 Ek= m v -do m,)1 积分后,得=十mc1-2-mc
三 质量与能量的关系 动能定理 2 0 2 k 2 1 2 1 E F dr mv mv x x p x p t p E F x k 0 0 0 d d d d d v 设 0 0 Ek 0 F Fi v0 2 0 2 0 2 0 k 1 1 m c m c m E 2 2 2 2 v c v c v 积分后,得 2 0 1 v m 利用 d( pv) pdv vdp 和 p v 2 v v v v 0 2 2 0 2 0 k d 1 1 c m m E 得

18-6相对论性动量和能量 第十八章相对论 =ym0 E=2+m,c2V1-2/c2-m,c2 相对论动能 Bx=me2-mc2=mc?( 当 0<<c时,Ek→。m1 相对论质能关系 E mc2 moc2+Ek 质能关系预言:物质的质量就是能量的一种储藏. 爱因斯坦认为(1905) 懒惰性>惯性(inertia) 物体的懒惰性就 活泼性→1 能量(energy 是物体活泼性的度量
1) 1 1 ( 2 2 0 2 0 2 k 相对论动能 E mc m c m c 2 k 0 2 1 当 v c 时, E m v m m 0 2 0 2 0 2 k E m m c 1 m c 2 2 v v c k 2 0 2 相对论质能关系 E mc m c E 爱因斯坦认为(1905) 懒惰性 惯性 ( inertia ) 活泼性 能量 ( energy ) 物体的懒惰性就 是物体活泼性的度量 . 质能关系预言:物质的质量就是能量的一种储藏