19-3康普顿效应 第十九章量子物理 1920年,美国物理学家康普顿在观察X射线被物质 散射时,发现散射线中含有波长发生变化了的成分 实验装置 ◆Replay
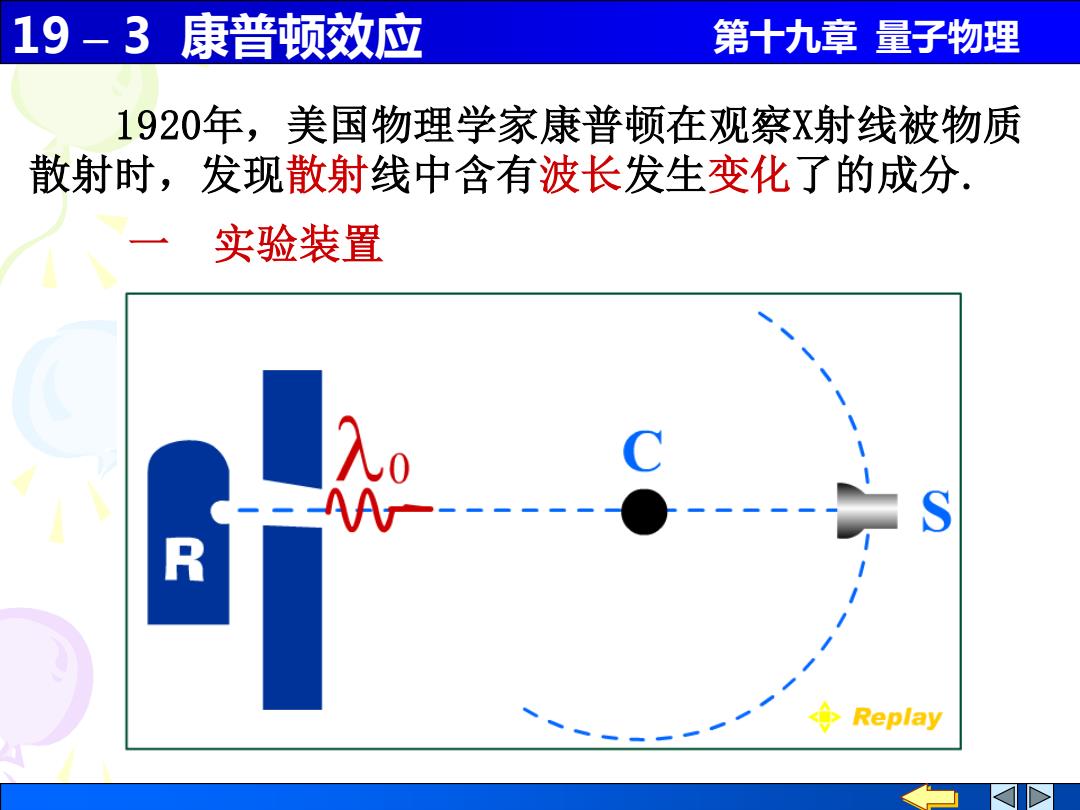
19 – 3 康普顿效应 第十九章 量子物理 1920年,美国物理学家康普顿在观察X射线被物质 散射时,发现散射线中含有波长发生变化了的成分. 一 实验装置
19-3 康普顿效应 第十九章量子物理 实验结果 【(相对强度) 0=0° 在散射X射线中除有 与入射波长相同的射线外, 还有波长比入射波长更长 0=45° 的射线. 三 经典理论的困难 0=90° 经典电磁理论预言, 散射辐射具有和入射辐射 0=135° 一样的频率.经典理论无 法解释波长变化. ,几(波长)
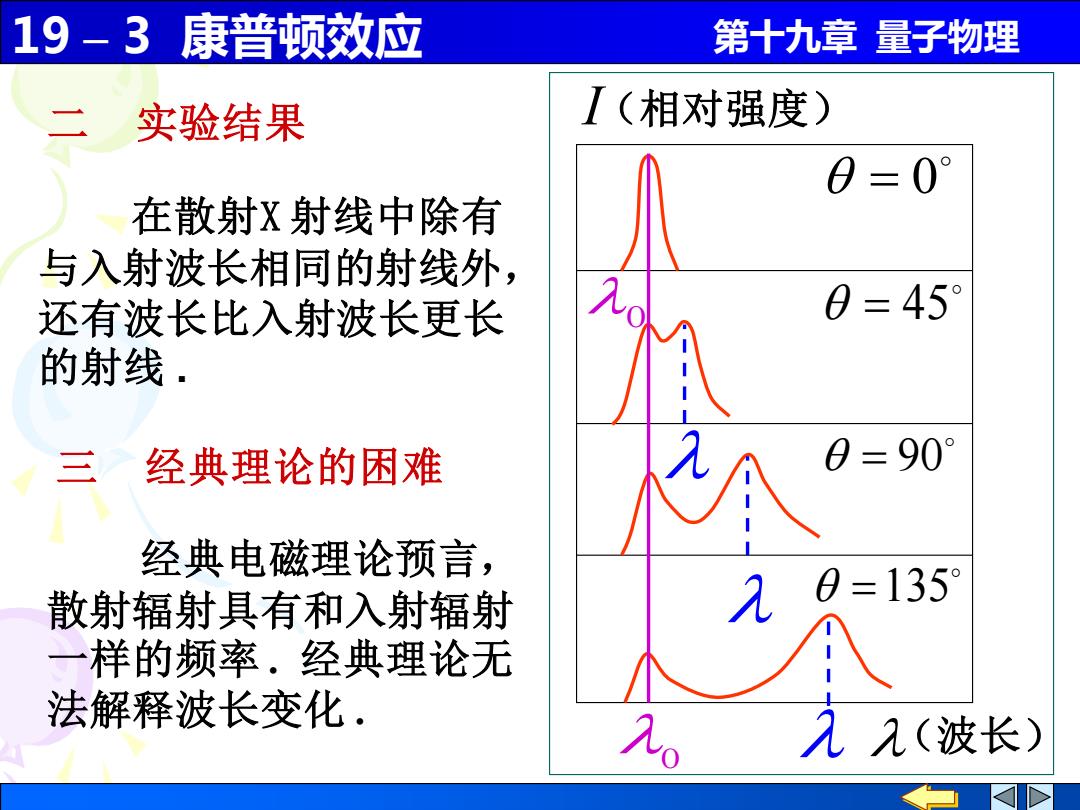
19 – 3 康普顿效应 第十九章 量子物理 经典电磁理论预言, 散射辐射具有和入射辐射 一样的频率 . 经典理论无 法解释波长变化 . 二 实验结果 = 0 = 45 = 90 =135 (相对强度) (波长) I 0 0 在散射X 射线中除有 与入射波长相同的射线外, 还有波长比入射波长更长 的射线 . 三 经典理论的困难

19-3康普顿效应 第十九章量子物理 四 量子解释 (1)物理模型 1 光子V 光子Vo M0电子 0=0 电子 ◆入射光子(X射线或Y射线)能量大· E=hv 范围为:104~105eV ◆固体表面电子束缚较弱,可视为近自由电子 ◆ 电子热运动能量<<hv,可近似为静止电子 ◆电子反冲速度很大,需用相对论力学来处理
19 – 3 康普顿效应 第十九章 量子物理 0 0 0 v = x y 光子 电子 电子反冲速度很大,需用相对论力学来处理. (1)物理模型 入射光子( X 射线或 射线)能量大 . 固体表面电子束缚较弱,可视为近自由电子. 四 量子解释 x y 电子 光子 电子热运动能量 h ,可近似为静止电子. 10 ~10 eV 4 5 E = h 范围为:

19-3康普顿效应 第十九章量子物理 (2)理论分析 hv 能量守恒 hvo +moc2 hv+mc2 hvo 动量守恒 hv es e+m⑦ mv ,h22 h"v c? 2 c cos 0 mcl-g)=md'-2M0-ws0+2<5-9 02
19 – 3 康普顿效应 第十九章 量子物理 2 cos 2 0 2 2 2 2 2 2 0 2 2 2 c h c h c h m v = + − (2)理论分析 x y 0 0 e c h e c h v m e 0 e 2 2 hv0 + m0 c = h + mc 能量守恒 v e m c h e c h = + 0 0 动量守恒 (1 ) 2 (1 cos ) 2 ( ) 0 2 0 0 2 4 2 2 0 2 2 4 − = m c − h − + m c h − c m c v

19-3康普顿效应 第十九章量子物理 m'c'(1-03)=m5c4-2ho1-cos0)+2m,ch,-y) m=m,(1-x21c2)12 c-C=h1-os0)=元-,=AM Vo m C >康普顿公式 A2=h(1-cos例=2hsn2 mc mc 2 康普顿波长2c= h=2.43×101m=2.43×103nm mc
19 – 3 康普顿效应 第十九章 量子物理 康普顿波长 2.43 10 m 2.43 10 nm 12 3 0 C − − = = = m c h (1 cos ) 0 0 − = − m c c c h (1 ) 2 (1 cos ) 2 ( ) 0 2 0 0 2 4 2 2 0 2 2 4 − = m c − h − + m c h − c m c v 2 2 1/ 2 0 (1 / ) − m = m − v c 2 sin 2 (1 cos ) 2 0 0 m c h m c h 康普顿公式 = − = = −0 =