
连续系统的嫩小值原理 极小值原理的表达 总结上述讨论,可将庞特里雅金极小值原理写为如下形式: 定理(极小值原理): 系统的状态方程为 X=fX,U,t)X()∈R” 初始条件为 X(to)=Xo 控制向量U)∈Rm,并受下面的约束 U∈2 终端约束 GX(),t=0 1口·1,之1三,至分只C 三章极小拉原速及其应用 最优控制理论与系统 November 9,2016 16/67
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 连续系统的极小值原理 极小值原理的表达 总结上述讨论,可将庞特里雅金极小值原理写为如下形式: 定理(极小值原理): 系统的状态方程为 X˙ = f(X, U, t) X(t) ∈ R n 初始条件为 X(t0) = X0 控制向量 U(t) ∈ Rm,并受下面的约束 U ∈ Ω 终端约束 G[X(tf), tf ] = 0 第三章 极小值原理及其应用 最优控制理论与系统 November 9, 2016 16 / 67

连续系统的费小值原理 极小值原理的表达 性能指标函数为 J=x幼,胡+'rxU,d 要求选择最优控制,使J取极小值。J取极小值的必要条件是X()、 )、入和t:满足下面的一组方程 1正则方程 i=- ∂H Ox (协态方程) (3-16) x= OH a入 (状态方程) (3-17) 2边界条件 X(to)=Xo G[X(),=0 (3-18) 3横截条件 00 aGt λ(t闭= 0Xt)∂Xt扮口·a、· (3-19) 第三章极小位原理及其应用 最优控制理论与系统 November 9,2016 17167
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 连续系统的极小值原理 极小值原理的表达 性能指标函数为 J = ϕ[X(tf), tf ] + ∫ tf t0 F(X, U, t) dt 要求选择最优控制 U∗,使 J 取极小值。J 取极小值的必要条件是 X(t)、 U(t)、λ 和 tf 满足下面的一组方程 1 正则方程 λ˙ = − ∂H ∂X (协态方程) (3-16) X˙ = ∂H ∂λ (状态方程) (3-17) 2 边界条件 X(t0) = X0 G[X(tf), tf ] = 0 (3-18) 3 横截条件 λ(tf) = ∂ϕ ∂X(tf) + ∂GT ∂X(tf) ν (3-19) 第三章 极小值原理及其应用 最优控制理论与系统 November 9, 2016 17 / 67
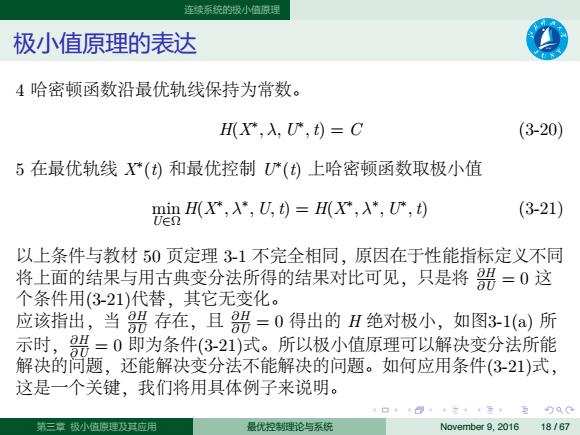
连续系统的嫩小值原理 极小值原理的表达 4哈密顿函数沿最优轨线保持为常数。 HX*,入,*,t)=C (3-20) 5在最优轨线X()和最优控制*()上哈密顿函数取极小值 X,X,U)=瓜X,",心, (3-21) 以上条件与教材50页定理3-1不完全相同,原因在于性能指标定义不同 将上面的结果与用古典变分法所得的结果对比可见,只是将號=0这 个条件用(3-21)代替,其它无变化。 应该指出,当號存在,且器=0得出的H绝对极小,如图3-1(a)所 示时,盟=0即为条件(3-21)式。所以极小值原理可以解决变分法所能 解决的问题,还能解决变分法不能解决的问题。如何应用条件(3-21)式, 这是一个关键,我们将用具体例子来说明。 三章极小拉原速及其应用 最优控制理论与系统 November 9,2016 18/67
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 连续系统的极小值原理 极小值原理的表达 4 哈密顿函数沿最优轨线保持为常数。 H(X ∗ , λ, U ∗ , t) = C (3-20) 5 在最优轨线 X∗ (t) 和最优控制 U∗ (t) 上哈密顿函数取极小值 min U∈Ω H(X ∗ , λ∗ , U, t) = H(X ∗ , λ∗ , U ∗ , t) (3-21) 以上条件与教材 50 页定理 3-1 不完全相同,原因在于性能指标定义不同 将上面的结果与用古典变分法所得的结果对比可见,只是将 ∂H ∂U = 0 这 个条件用(3-21)代替,其它无变化。 应该指出,当 ∂H ∂U 存在,且 ∂H ∂U = 0 得出的 H 绝对极小,如图3-1(a) 所 示时,∂H ∂U = 0 即为条件(3-21)式。所以极小值原理可以解决变分法所能 解决的问题,还能解决变分法不能解决的问题。如何应用条件(3-21)式, 这是一个关键,我们将用具体例子来说明。 第三章 极小值原理及其应用 最优控制理论与系统 November 9, 2016 18 / 67
是短时间控葫问题 最短时间控制问题 节省时间意味着提高生产率或先发制人取得军事行动的胜利。所以人们 很早就开始了对最短时间控制的研究,这方面的研究结果很多,这里先 就简单的重积分系统的最短时间控制展开讨论。 在前面的绪论中列举了火车快速行驶问题。设火车质量m=1,把运动 方程写成状态方程形式,令=x,2=x可化为下面的最短时间控制 问题。 口4得,二4三至)Q0 第三章极小值原理及其应用 最优控制理论与系统 November 9,2016 19/67
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 最短时间控制问题 最短时间控制问题 节省时间意味着提高生产率或先发制人取得军事行动的胜利。所以人们 很早就开始了对最短时间控制的研究,这方面的研究结果很多,这里先 就简单的重积分系统的最短时间控制展开讨论。 在前面的绪论中列举了火车快速行驶问题。设火车质量 m = 1,把运动 方程写成状态方程形式,令 x1 = x,x2 = x˙ 可化为下面的最短时间控制 问题。 第三章 极小值原理及其应用 最优控制理论与系统 November 9, 2016 19 / 67

最短时闻控制问题 重积分系统的最短时间控制 例3-1 状态方程 =2 i =u (3-22) 初始条件为 (t0)=20 2(to)=20 (3-23) 终端条件为 m(=0 2()=0 (3-24) 控制约束为 lu(t训≤1o≤t≤t (3-25) 求出使性能指标 J- dt=t-o (3-26) 三章极小拉原及其应用 最优控制理论与系统 November9.,201620/67
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 最短时间控制问题 重积分系统的最短时间控制 例 3 - 1 状态方程 x˙1 = x2 x˙2 = u (3-22) 初始条件为 x1(t0) = x10 x2(t0) = x20 (3-23) 终端条件为 x1(tf) = 0 x2(tf) = 0 (3-24) 控制约束为 |u(t)| ≤ 1 t0 ≤ t ≤ tf (3-25) 求出使性能指标 J = ∫ tf t0 dt = tf − t0 (3-26) 第三章 极小值原理及其应用 最优控制理论与系统 November 9, 2016 20 / 67