
第四节线性方程组的解的结构 2.教学基本要求: 通过本章教学使学生能较好地掌捉N维向量,V维向量空间,向量间的线性关系(线性 组合、线性相关,线性无关),向量组的秩,向量组的极大无关组,线性方程组解的结构等基础 知识。 1、了解N维向量与N维向量空间的概念,掌握N维向量的线性运算。 2、了解向量组的线性相关性与线性无关性,会判断一个向量组是否线性相关。 3、掌握用初等变换的方法求向量组的极大无关组及向量组的秩。 4、了解线性方程组的一般形式与矩阵形式,知道线性方程组有解的判定定理,掌握用初等 变换的方法求方程组通解的方法。 3.教学重点难点: 向量组的线性相关性与线性无关性,用初等变换的方法求向量组的极大无关组、向量组的 秩及解线性方程组。 4.教学建议:应重点掌握:(1)向量组的线性相关性与线性无关性:(2)向量组的极大无关组 第四章:矩阵的特征值与特征向量 1.基本内容: 第一节方阵的特征值与特征向量 第二节向量的内积与向量组的正交规范化 第三节矩阵对角化 2.教学基本要求: 通过本章教学使学生了解和掌握矩阵的特征值与特征向量,相似矩阵,实对称矩阵的特征 值与特征向量,正交向量组,正交矩阵等知识。 1、理解矩阵的特征值与特征向量的概念,掌握求特征值与特征向量的方法,了解特征值与 特征向量的性质。 2、理解相似矩阵的概念,了解相似矩阵的性质,知道一个矩阵与对角矩阵相似的条件。 3、了解正交向量组的概念,理解正交矩阵的概念,知道正交矩阵的性质。 4、掌握实对称矩阵化为对角矩阵的方法。 3.教学重点难点: 矩阵的特征值与特征向量的概念,求特征值与特征向量的方法,施密特正交化方法,方阵 对角化的条件与方法。 4.教学建议:矩阵的特征值与特征向量的概念比较难以掌握,尽量通过几何方法给出解释。 第五章:二次型 22
第四节 线性方程组的解的结构 2. 教学基本要求: 通过本章教学使学生能较好地掌握 N 维向量,N 维向量空间,向量间的线性关系(线性 组合、线性相关,线性无关),向量组的秩,向量组的极大无关组,线性方程组解的结构等基础 知识。 1、了解 N 维向量与 N 维向量空间的概念,掌握 N 维向量的线性运算。 2、了解向量组的线性相关性与线性无关性,会判断一个向量组是否线性相关。 3、掌握用初等变换的方法求向量组的极大无关组及向量组的秩。 4、了解线性方程组的一般形式与矩阵形式,知道线性方程组有解的判定定理,掌握用初等 变换的方法求方程组通解的方法。 3. 教学重点难点: 向量组的线性相关性与线性无关性,用初等变换的方法求向量组的极大无关组、向量组的 秩及解线性方程组。 4. 教学建议:应重点掌握:(1)向量组的线性相关性与线性无关性;(2)向量组的极大无关组。 第四章:矩阵的特征值与特征向量 1. 基本内容: 第一节 方阵的特征值与特征向量 第二节 向量的内积与向量组的正交规范化 第三节 矩阵对角化 2. 教学基本要求: 通过本章教学使学生了解和掌握矩阵的特征值与特征向量,相似矩阵,实对称矩阵的特征 值与特征向量,正交向量组,正交矩阵等知识。 1、理解矩阵的特征值与特征向量的概念,掌握求特征值与特征向量的方法,了解特征值与 特征向量的性质。 2、理解相似矩阵的概念,了解相似矩阵的性质,知道一个矩阵与对角矩阵相似的条件。 3、了解正交向量组的概念,理解正交矩阵的概念,知道正交矩阵的性质。 4、掌握实对称矩阵化为对角矩阵的方法。 3. 教学重点难点: 矩阵的特征值与特征向量的概念,求特征值与特征向量的方法,施密特正交化方法,方阵 对角化的条件与方法。 4. 教学建议:矩阵的特征值与特征向量的概念比较难以掌握,尽量通过几何方法给出解释。 第五章:二次型 22
1.基本内容: 第一节二次型的概念 第二节二次型标准化 2.教学基本要求: 1、理解二次型的概念,二次型对应矩阵,正负惯性指数 2、理解正定二次型的概念及判断。 3、掌握二次型化标准型的方法。 3.教学重点难点: 正定二次型的概念及判断, 二次型化标准型的方法 4.教学建议:正定二次型的概念难以理解,因此建议尽量结合应用意义去解释该概念 四、教学环节与学时分配 其 序号 教学内容 总学时 讲课习题课其他 备注 1 第一章行列式 7 第二章矩阵 10 8 2 第三章向量的线性相关性 与线性方程组的解的结构 10 8 第四章矩阵的特征值与特 4 征向 6 第五章二次型 6 4 五、教学中应注意的问题:线性代数比较抽象,要注意结合几何意义。 六、实验实践内容:无。 七、考核方式:见《线性代数》课程考试大纲。 八、教材及主要参考书: 1、选用教材: 《线性代数》同济大学应用数学系主编,高等教育出版社,2007年 《线性代数》谭琼华主编,复旦大学出版社,2010年 2、主要参考书: 《高等代数》,北京大学数学系主编,高等教有出版社,1988。 《线性代数学习辅导与习题解答》,吴赣吕主编,中国人民大学出版社,2010 《线性代数及应用》,谢国瑞主编,高等教育出版社,1999. (Linear Algebra And Its Application),David C.Lay.1995 九、教改说明及其他:强烈要求增加教学课时,否则无法完成教学任务 23
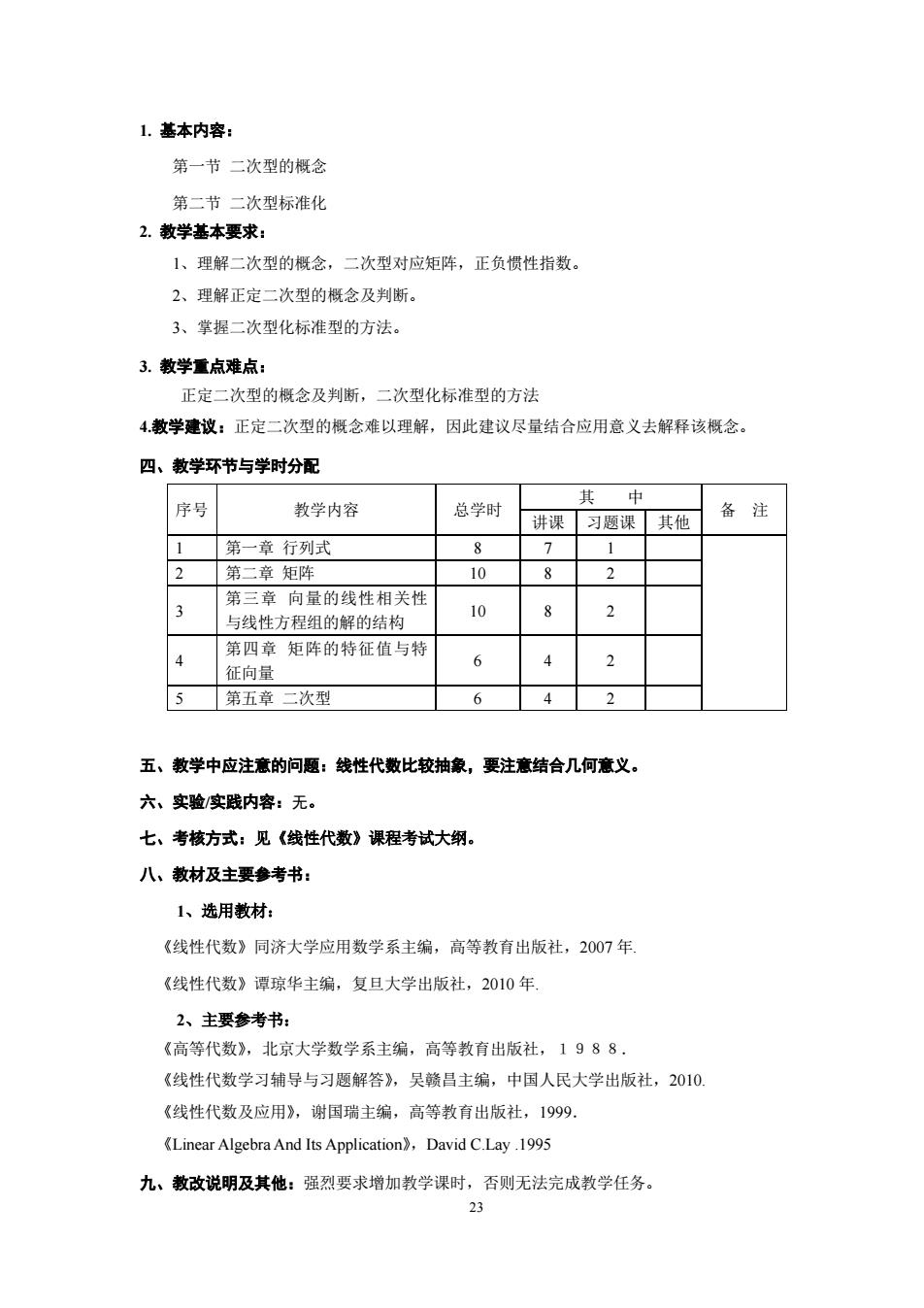
1. 基本内容: 第一节 二次型的概念 第二节 二次型标准化 2. 教学基本要求: 1、理解二次型的概念,二次型对应矩阵,正负惯性指数。 2、理解正定二次型的概念及判断。 3、掌握二次型化标准型的方法。 3. 教学重点难点: 正定二次型的概念及判断,二次型化标准型的方法 4.教学建议:正定二次型的概念难以理解,因此建议尽量结合应用意义去解释该概念。 四、教学环节与学时分配 序号 教学内容 总学时 其 中 备 注 讲课 习题课 其他 1 第一章 行列式 8 7 1 2 第二章 矩阵 10 8 2 3 第三章 向量的线性相关性 与线性方程组的解的结构 10 8 2 4 第四章 矩阵的特征值与特 征向量 6 4 2 5 第五章 二次型 6 4 2 五、教学中应注意的问题:线性代数比较抽象,要注意结合几何意义。 六、实验/实践内容:无。 七、考核方式:见《线性代数》课程考试大纲。 八、教材及主要参考书: 1、选用教材: 《线性代数》同济大学应用数学系主编,高等教育出版社,2007 年. 《线性代数》谭琼华主编,复旦大学出版社,2010 年. 2、主要参考书: 《高等代数》,北京大学数学系主编,高等教育出版社,1988. 《线性代数学习辅导与习题解答》,吴赣昌主编,中国人民大学出版社,2010. 《线性代数及应用》,谢国瑞主编,高等教育出版社,1999. 《Linear Algebra And Its Application》,David C.Lay .1995 九、教改说明及其他:强烈要求增加教学课时,否则无法完成教学任务。 23

执笔人:郑立景系室审核人:王恒太 24
执笔人:郑立景 系室审核人:王恒太 24

《线性代数》课程考试大纲 课程编号:130704016 总学时数:40学时学分:2.5学分 一、考试对象 修完本课程所规定的各专业学生。 二、考试目的 本课程考试目的是考核学生对线性代数的基本概念、基本理论的理解程度:考核学生掌握 线性代数中处理离散量的基本方法及其熟练程度:考核学生综合运用所学知识分析问题和解决 问题的能力。 三、考试要求 本课程是一门抽象程度很高的基础理论学科,要求学生认识和理解相关基本理论,掌握行 列式、矩阵两个数学工具,并能应用这两个工具(尤其是矩阵)解决向量空间、线性方程组的 相关问题。 四、考试内容与要求 第一章行列式15-20分值 1、考试内容:①行列式的概念:②行列式的性质:③行列式按行(列)展开定理:④克 莱姆法则。 2、考试要求: ①识记行列式的概念、余子式代数余子式的概念,会计算排列的逆序数: ②掌握行列式的性质,并会利用行列式的性质计算行列式: ③掌握行列式按行(列)展开定理,并会利用展开定理计算行列式: ④会用克莱姆法则求解线性方程组。 第二章矩阵 25-30分值 1、考试内容:①矩阵的概念:②矩阵的线性运算,矩阵的乘法,方阵的幂,方阵乘积的行 列式,矩阵的转置,分块矩阵及其运算:③伴随矩阵,逆矩阵的概念和性质:矩阵可逆的充要 条件:④矩阵的秩,矩阵的初等变换的概念,矩阵的等价,初等矩阵的概念:⑤齐次线性方程 组有非零解的充分必要条件,非齐次线性方程组有解的充分必要条件。 2、考试要求: ①理解矩阵的概念,识记单位矩阵、数量矩阵、对角矩阵、三角矩阵、对称矩阵的定义和 25
《线性代数》课程考试大纲 课程编号:130704016 总学时数:40 学时 学分:2.5 学分 一、考试对象 修完本课程所规定的各专业学生。 二、考试目的 本课程考试目的是考核学生对线性代数的基本概念、基本理论的理解程度;考核学生掌握 线性代数中处理离散量的基本方法及其熟练程度;考核学生综合运用所学知识分析问题和解决 问题的能力。 三、考试要求 本课程是一门抽象程度很高的基础理论学科,要求学生认识和理解相关基本理论,掌握行 列式、矩阵两个数学工具,并能应用这两个工具(尤其是矩阵)解决向量空间、线性方程组的 相关问题。 四、考试内容与要求 第一章 行列式 15-20 分值 1、考试内容: ①行列式的概念;②行列式的性质;③ 行列式按行(列)展开定理;④克 莱姆法则。 2、考试要求: ①识记行列式的概念、余子式代数余子式的概念,会计算排列的逆序数; ②掌握行列式的性质,并会利用行列式的性质计算行列式; ③掌握行列式按行(列)展开定理,并会利用展开定理计算行列式; ④会用克莱姆法则求解线性方程组。 第二章 矩阵 25-30 分值 1、考试内容:①矩阵的概念;②矩阵的线性运算,矩阵的乘法,方阵的幂,方阵乘积的行 列式,矩阵的转置,分块矩阵及其运算;③伴随矩阵,逆矩阵的概念和性质;矩阵可逆的充要 条件;④矩阵的秩,矩阵的初等变换的概念,矩阵的等价,初等矩阵的概念;⑤齐次线性方程 组有非零解的充分必要条件,非齐次线性方程组有解的充分必要条件。 2、考试要求: ①理解矩阵的概念,识记单位矩阵、数量矩阵、对角矩阵、三角矩阵、对称矩阵的定义和 25

性质: ②掌握矩阵的线性运算、乘法、转置以及它们的运算规律,理解方阵的幂与方阵乘积行列 式的性质,理解分块矩阵的概念及其运算: ③理解逆矩阵的概念,掌握逆矩阵的性质以及矩阵可逆的充要条件:理解件随矩阵的概念 会用伴随矩阵求逆矩阵: ④理解矩阵秩的概念,掌握矩阵秩的性质: ⑤理解矩阵的初等变换的概念,了解初等矩阵的性质和矩阵等价的概念 ⑥了解非零矩阵的行阶梯形与行最简形的概念: ⑦掌握用初等行变换法求矩阵的秩和逆矩阵的方法: ⑧理解齐次线性方程组有非零解的充分必要条件,理解非齐次线性方程组有解的充分必要 条件: ⑨掌握用初等行变换法求解线性方程组的方法。 第三章向量组的线性相关性与线性方程组的解的结构 25-30分值 1、考试内容:①向量的概念,向量的线性组合与线性表示,向量组的线性相关与线性无 关,等价向量组:②向量组的最大线性无关组,向量组的秩,向量组的秩与矩阵秩的关系:③ 向量空间的概念及相关概念:④线性方程组解的性质和解的结构,齐次线性方程组的基础解系 和通解,非齐次线性方程组的通解。 2、考试要求: ①理解n维向量、向量的线性组合与线性表示的概念: ②理解向量组线性相关、线性无关的概念,掌握向量组线性相关、线性无关的有关性质及 判别法: ③理解向量组的最大线性无关组和向量组的秩的概念,会求向量组的最大线性无关组及秩, 理解向量组等价的概念,理解矩阵的秩与其行(列)向量组的秩之间的关系: ④了解向量空间、向量空间的基与维数的概念 ⑤理解齐次线性方程组的基础解系、通解的概念,掌握齐次线性方程组的基础解系和通解 的求法:理解非齐次线性方程组解的结构及通解的概念。 第四章矩阵的特征值与特征向量 15-20分值 1、考试内容:①矩阵的特征值和特征向量的概念、性质:②向量的内积,正交矩阵及其 性质,规范正交基,线性无关向量组的正交规范化方法:③相似变换、相似矩阵的概念及性质: 矩阵可相似对角化的充分必要条件及矩阵对角化方法:④实对称矩阵的特征值、特征向量及其 相似对角矩阵。 26
性质; ②掌握矩阵的线性运算、乘法、转置以及它们的运算规律,理解方阵的幂与方阵乘积行列 式的性质,理解分块矩阵的概念及其运算; ③理解逆矩阵的概念,掌握逆矩阵的性质以及矩阵可逆的充要条件;理解伴随矩阵的概念, 会用伴随矩阵求逆矩阵; ④理解矩阵秩的概念,掌握矩阵秩的性质; ⑤理解矩阵的初等变换的概念,了解初等矩阵的性质和矩阵等价的概念; ⑥了解非零矩阵的行阶梯形与行最简形的概念; ⑦掌握用初等行变换法求矩阵的秩和逆矩阵的方法; ⑧理解齐次线性方程组有非零解的充分必要条件,理解非齐次线性方程组有解的充分必要 条件; ⑨掌握用初等行变换法求解线性方程组的方法。 第三章 向量组的线性相关性与线性方程组的解的结构 25-30 分值 1、考试内容:①向量的概念,向量的线性组合与线性表示,向量组的线性相关与线性无 关,等价向量组;②向量组的最大线性无关组,向量组的秩,向量组的秩与矩阵秩的关系;③ 向量空间的概念及相关概念;④线性方程组解的性质和解的结构,齐次线性方程组的基础解系 和通解,非齐次线性方程组的通解。 2、考试要求: ①理解n 维向量、向量的线性组合与线性表示的概念; ②理解向量组线性相关、线性无关的概念,掌握向量组线性相关、线性无关的有关性质及 判别法; ③理解向量组的最大线性无关组和向量组的秩的概念,会求向量组的最大线性无关组及秩, 理解向量组等价的概念,理解矩阵的秩与其行(列)向量组的秩之间的关系; ④了解向量空间、向量空间的基与维数的概念. ⑤理解齐次线性方程组的基础解系、通解的概念,掌握齐次线性方程组的基础解系和通解 的求法;理解非齐次线性方程组解的结构及通解的概念。 第四章 矩阵的特征值与特征向量 15-20 分值 1、考试内容:①矩阵的特征值和特征向量的概念、性质;②向量的内积,正交矩阵及其 性质,规范正交基,线性无关向量组的正交规范化方法;③相似变换、相似矩阵的概念及性质; 矩阵可相似对角化的充分必要条件及矩阵对角化方法;④实对称矩阵的特征值、特征向量及其 相似对角矩阵。 26