
Lyman 氢原子光谱由五组线系组成,即紫外☒ ,=1) 的莱曼(Lyman)系,可见区的巴尔麦 (Balmer)系,红外区的帕邢(Paschen系、布 莱克特(Brackett)系和芬得Pfund)系.任何 一条谱线的波数(wave number)都满足简单 的经验关系式: 巴尔麦经验公式立=R 1 Brackett 式中v为波数的符号,它定义为波长的倒数,单位常用cm;R为里德 伯常量,实验确定为1.09677×107m;n2大于n1,二者都是不大的正 整数.各线系n的允许值见下表: 例如:对于Balmer线系的处理 The allowed values for n in above equation v=3.289×1015 Name n n2 Lyman series 23.4. n=3 红 (Ha) Balmer series 3.45. n=4 青 Paschen series 45,6 (HB) Brackett series 5,6,7 n=5 蓝紫 (H) Pfund series 6.7,8. n=6 紫 (H) 上页 下页 节首 节尾
21 氢原子光谱由五组线系组成, 即紫外区 的 莱 曼 ( Lyman) 系 , 可 见 区 的 巴 尔 麦 (Balmer)系, 红外区的帕邢(Paschen)系、布 莱克特(Brackett)系和芬得(Pfund)系. 任何 一条谱线的波数(wave number)都满足简单 的经验关系式: = = − 2 2 2 1 ~ 1 1 1 n n RH 巴尔麦经验公式 式中v为波数的符号, 它定义为波长的倒数, 单位常用cm-1 ; RH为里德 伯常量, 实验确定为1.096 77×107 m-1 ; n2大于n1 , 二者都是不大的正 整数.各线系 n 的允许值见下表: The allowed values for n in above equation Name n1 n2 Lyman series Balmer series Paschen series Brackett series Pfund series 1 2 3 4 5 2,3,4,. 3,4,5,. 4,5,6,. 5,6,7,. 6,7,8,. 例如:对于Balmer线系的处理 1 2 2 15 )s 1 2 1 3.289 10 ( − = − n v n = 3 红 (Hα) n = 4 青 (Hβ ) n = 5 蓝紫 ( Hγ ) n = 6 紫 (Hδ )
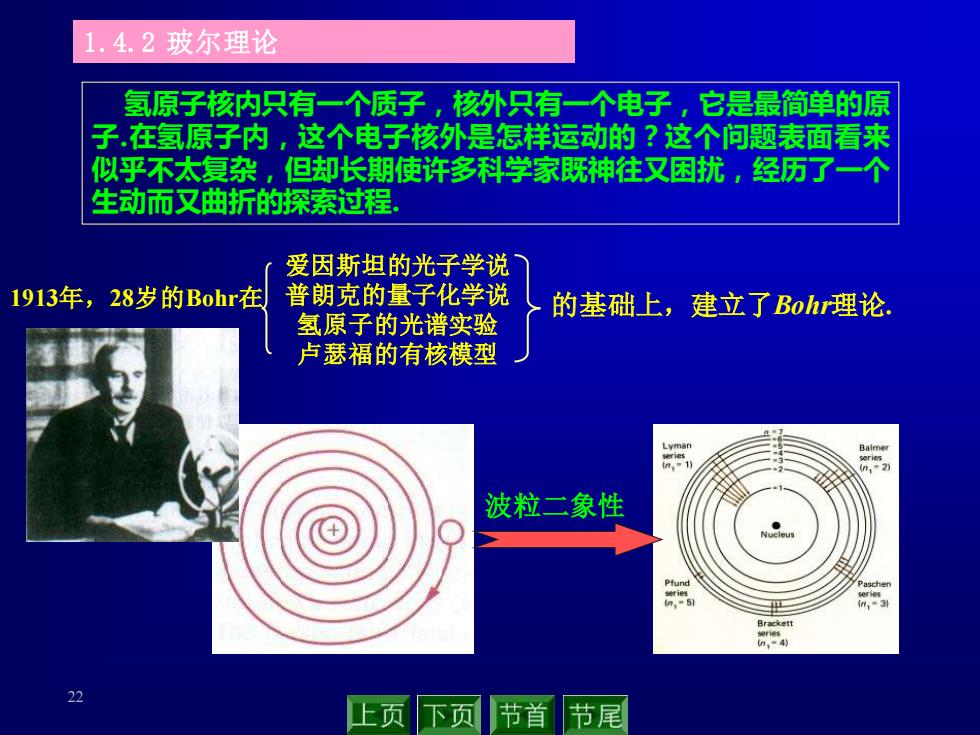
4.2玻尔理论 氢原子核内只有一个质子,核外只有一个电子,它是最简单的原 子,在氢原子内,这个电子核外是怎样运动的?这个问题表面看来 似乎不太复杂,但却长期使许多科学家既神往又困扰,经历了一个 生动而又曲折的探索过程 爱因斯坦的光子学说 1913年,28岁的Bohr在 普朗克的量子化学说 的基础上,建立了Bohr理论: 氢原子的光谱实验 卢瑟福的有核棋型 波粒二象性 Br 22 上页 下页 节首 节尾
22 氢原子核内只有一个质子,核外只有一个电子,它是最简单的原 子.在氢原子内,这个电子核外是怎样运动的?这个问题表面看来 似乎不太复杂,但却长期使许多科学家既神往又困扰,经历了一个 生动而又曲折的探索过程. 爱因斯坦的光子学说 普朗克的量子化学说 氢原子的光谱实验 卢瑟福的有核模型 1913年,28岁的Bohr在 的基础上,建立了Bohr理论. 波粒二象性 1.4.2 玻尔理论

Bohr理论的主要内容 年轻的丹麦物理学家玻尔(Bohr N,1885-1962)于1913年提出的 氢原子结构的量子力学模型是基于下述3条假定: ★关于固定轨道的概念.玻尔模型认为,电子只能在若干圆形的固定 轨道上绕核运动.因此,玻尔的氢原子模型可以形象地称为行星模 型。固定轨道是指符合一定条件的轨道,这个条件是,电子的轨道 角动量L只能等于h/(2)的整数倍: h mvr= 2π 式中m和v分别代表电子的质量和速度,r为轨道半径,h为普朗 克常量,n叫做量子数(quantum number),取1,2,3,.等正整数.轨道 角动量的量子化意味着轨道半径受量子化条件的制约,图中示出的 这些固定轨道,从距核最近的一条轨道算起,n值分别等于 1,2,3,4,5,6,7.根据假定条件算得n=1时允许轨道的半径为53pm, 2这就是著名的玻尔半径 页下页节首节尾
23 Bohr 理论的主要内容 年轻的丹麦物理学家玻尔(Bohr N,1885-1962)于1913年提出的 氢原子结构的量子力学模型是基于下述3条假定: ★ 关于固定轨道的概念. 玻尔模型认为, 电子只能在若干圆形的固定 轨道上绕核运动.因此,玻尔的氢原子模型可以形象地称为行星模 型。 固定轨道是指符合一定条件的轨道, 这个条件是, 电子的轨道 角动量L只能等于h/(2)的整数倍: 2 h L = mvr = n 式中 m 和 v 分别代表电子的质量和速度, r 为轨道半径, h 为普朗 克常量, n 叫做量子数(quantum number), 取1,2,3,.等正整数. 轨道 角动量的量子化意味着轨道半径受量子化条件的制约, 图中示出的 这些固定轨道, 从距核最近的一条轨道算起, n值分别等于 1,2,3,4,5,6,7. 根据假定条件算得 n = 1 时允许轨道的半径为 53 pm, 这就是著名的玻尔半径

★关于轨道能量量子化的概念.电子轨道角动量的量子化也意味着 能量量子化.即原子只能处于上述条件所限定的几个能态,不可 能存在其他能态 定态(stationary state): 所有这些允许能态之统称.核外电子只能在有确定半径和能量的 定态轨道上运动,且不辐射能量 基态(groundstate): n值为1的定态.通常电子保持在能量最低的这一基态.基态是 能量最低即最稳定的状态 激发态(excitedstates): 指除基态以外的其余定态.各激发态的能量随值增大而增 高.电子只有从外部吸收足够能量时才能到达激发态 24 上页 页 节首 节尾
24 ★关于轨道能量量子化的概念. 电子轨道角动量的量子化也意味着 能量量子化. 即原子只能处于上述条件所限定的几个能态, 不可 能存在其他能态. 指除基态以外的其余定态. 各激发态的能量随 n 值增大而增 高. 电子只有从外部吸收足够能量时才能到达激发态. 定态(stationary state): 所有这些允许能态之统称.核外电子只能在有确定半径和能量的 定态轨道上运动,且不辐射能量. 基态(ground state): n 值为 1 的定态.通常电子保持在能量最低的这一基态. 基态是 能量最低即最稳定的状态. 激发态(excited states):

★关于能量的吸收和发射, 玻尔模型认为,只有当电子从较高能态(E)向较低能态(E) 跃迁时,原子才能以光子的形式放出能量(即,定态轨道上运动 的电子不放出能量),光子能量的大小决定于跃迁所涉及的两条 轨道间的能量差。根据普朗克关系式,该能量差与跃迁过程产生 的光子的频率互成正比: △E=E2-E,= 如果电子由能量为的轨道跃至能量为E,的轨道,显然应从外 部吸收同样的能量。 -E=0.0 ev,n= hv=E2-E E=-0.544eV,n=5 -0.850eV,n=4 v=E- E=-1.510cV.n=3 E=-3.399eV.n▣2 h E:轨道的能量 y:光的频率 h:Planck常数 E=-13.595eV.n=1 6.626x10-34J.S 上页 节首 节尾
25 ★ 玻尔模型认为, 只有当电子从较高能态(E2 )向较低能态(E1 ) 跃迁时, 原子才能以光子的形式放出能量(即, 定态轨道上运动 的电子不放出能量), 光子能量的大小决定于跃迁所涉及的两条 轨道间的能量差. 根据普朗克关系式, 该能量差与跃迁过程产生 的光子的频率互成正比: 关于能量的吸收和发射. ΔE = E2 - E1 = 如果电子由能量为hEν 1的轨道跃至能量为E2的轨道, 显然应从外 部吸收同样的能量. h E E h E E 2 1 2 1 − = = − E: 轨道的能量 ν:光的频率 h: Planck常数 6.626x10-34J.S