
布铲产销平衡条作下,可知24一习 (2) 如果立4≠立6,就称此运输 m MinZ=∑∑cX, 问题为非平衡运输问题,包含 产大于销和销大于产两种情况, X,=a=12,m j 这我们将在第三节介绍。 (3) 下面我们只考虑产销平衡s.t 2x,=6,U=12m) 问题,产销平衡运输问题的一 般模型为: X≥0(i=1,2,m,j=1,2,,n) 其中约束条件右端常数a:和b满足(2),在运输问题(3) 中,目标函数要求运输总费用最小;前个约束条件的意义 是:由某一产地运往各个销地的物资数量之和等于该产地的 产量;中间个约束条件的意义是:由各产地运往某一销地 的物资数量之和等于该销地的销量;后mn个约束条件是变量 的非负条件 12
12 如果 ,就称此运输 问题为非平衡运输问题,包含 产大于销和销大于产两种情况, 这我们将在第三节介绍。 下面我们只考虑产销平衡 问题,产销平衡运输问题的一 般模型为: 0 ( 1,2, , ; 1,2, , ) ( 1,2, , ) ( 1,2, , ) . Min 1 1 1 1 X i m j n X b j n X a i m st Z c X ij m i ij j n j ij i m i n j ij ij 在产销平衡条件下,可知 n j j m i ai b 1 1 (2) n j j m i ai b 1 1 其中约束条件右端常数ai 和bj满足(2),在运输问题(3) 中,目标函数要求运输总费用最小;前m个约束条件的意义 是:由某一产地运往各个销地的物资数量之和等于该产地的 产量;中间n个约束条件的意义是:由各产地运往某一销地 的物资数量之和等于该销地的销量;后mn个约束条件是变量 的非负条件. (3)
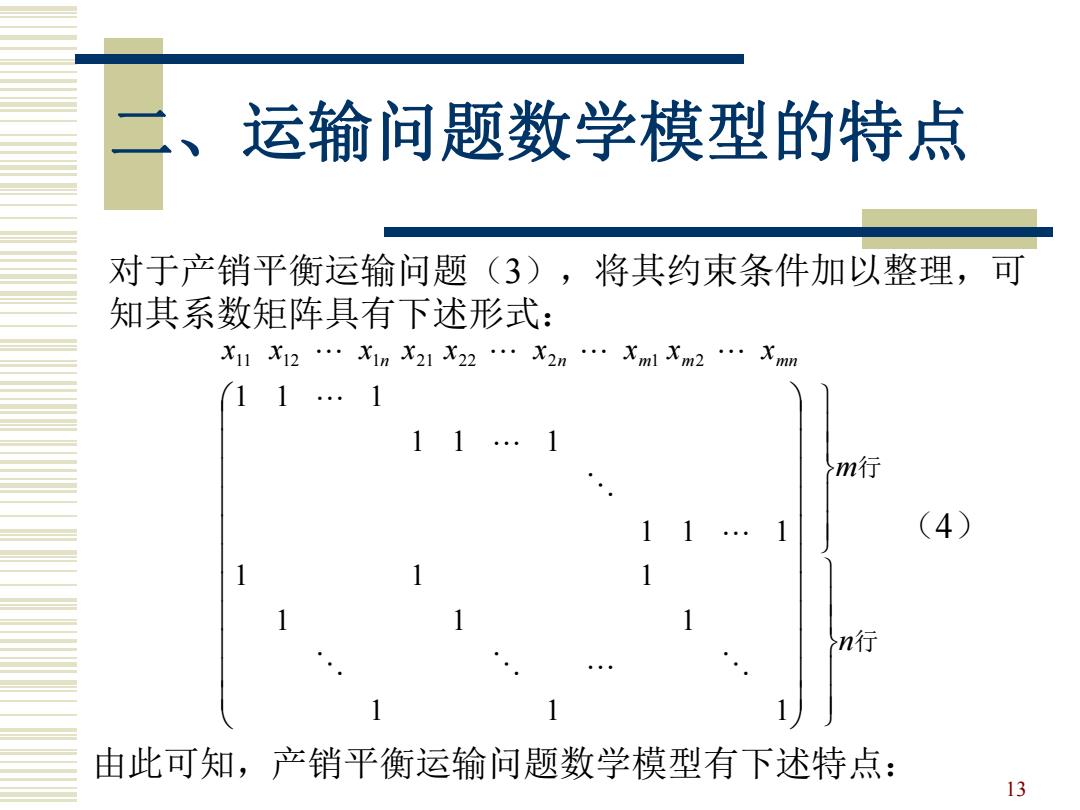
运输问题数学模型的特点 对于产销平衡运输问题(3),将其约束条件加以整理,可 知其系数矩阵具有下述形式: X11X12·X1nX21X22·X2nXm1Xm2·Xmm 11.1 11 m行 (4) n行 由此可知,产销平衡运输问题数学模型有下述特点: 13
13 二、运输问题数学模型的特点 对于产销平衡运输问题(3),将其约束条件加以整理,可 知其系数矩阵具有下述形式: 行 行 n m x x x x x x x x x n n m m mn 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 11 12 1 21 22 2 1 2 (4) 由此可知,产销平衡运输问题数学模型有下述特点:
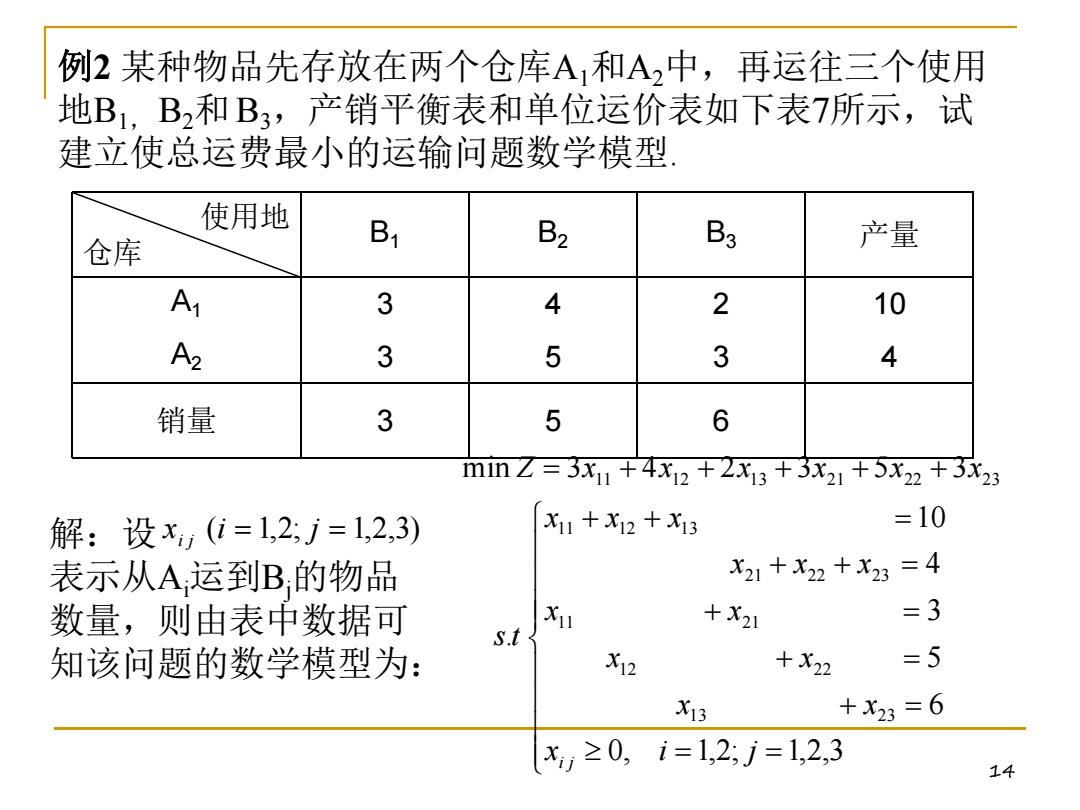
例2某种物品先存放在两个仓库A,和A中,再运往三个使用 地B1,B,和B,产销平衡表和单位运价表如下表7所示,试 建立使总运费最小的运输问题数学模型 使用地 仓库 B1 B2 B3 产量 A 3 4 2 10 A2 3 5 3 4 销量 3 5 6 mmZ=3x1+4x12+2x13+3x21+5x22+3x29 解:设x(i=1,2,j=1,2,3) x11+X12+x13 =10 表示从A运到B的物品 X21+X22+x23=4 数量,则由表中数据可 Xu +X21 =3 知该问题的数学模型为: X12 +X22 =5 X13 +X23=6 xy≥0,i=1,2j=1,2,3 14
14 例2 某种物品先存放在两个仓库A1和A2中,再运往三个使用 地B1, B2和B3,产销平衡表和单位运价表如下表7所示,试 建立使总运费最小的运输问题数学模型. 使用地 仓库 B1 B2 B3 产量 A1 3 4 2 10 A2 3 5 3 4 销量 3 5 6 解:设 表示从Ai运到Bj的物品 数量,则由表中数据可 知该问题的数学模型为: x (i 1,2; j 1,2,3) i j 0, 1,2; 1,2,3 6 5 3 4 10 . min 3 4 2 3 5 3 13 23 12 22 11 21 21 22 23 11 12 13 11 12 13 21 22 23 x i j x x x x x x x x x x x x st Z x x x x x x i j
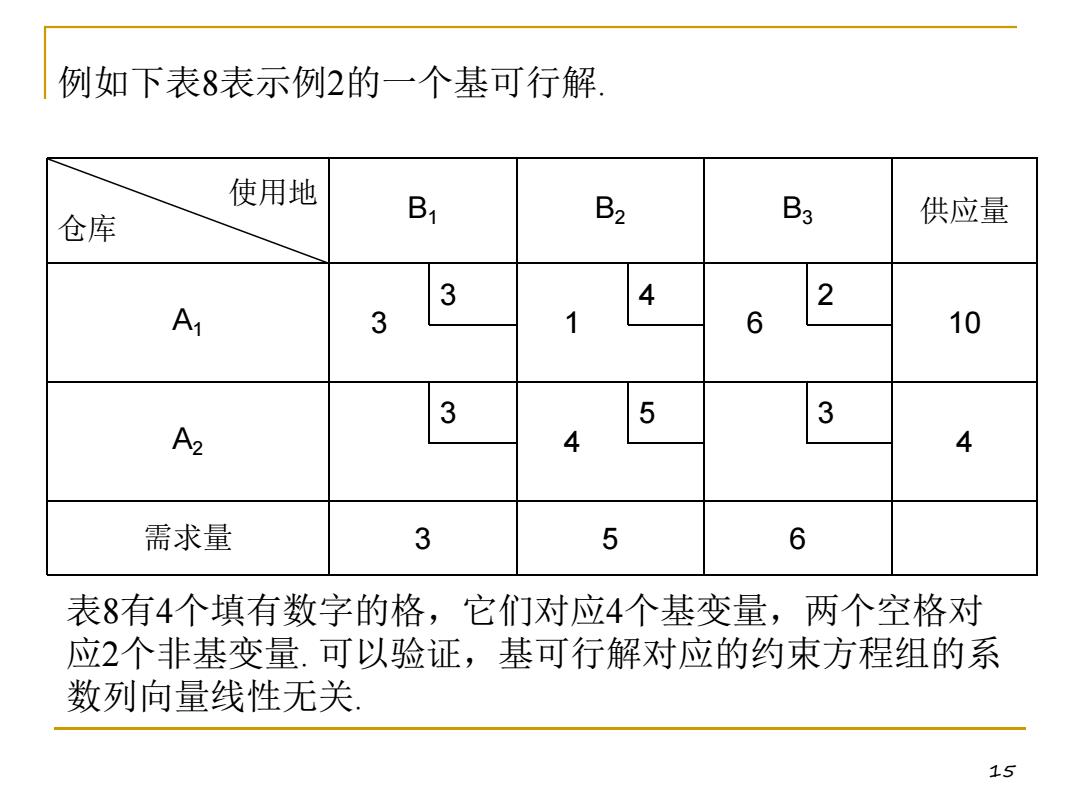
例如下表8表示例2的一个基可行解 使用地 仓库 B1 B2 B3 供应量 3 2 A 3 1 6 10 3 5 3 A2 4 4 需求量 3 5 6 表8有4个填有数字的格,它们对应4个基变量,两个空格对 应2个非基变量.可以验证,基可行解对应的约束方程组的系 数列向量线性无关」 15
15 例如下表8表示例2的一个基可行解. 使用地 仓库 B1 B2 B3 供应量 A1 3 3 1 4 6 2 10 A2 3 4 5 3 4 需求量 3 5 6 表8有4个填有数字的格,它们对应4个基变量,两个空格对 应2个非基变量. 可以验证,基可行解对应的约束方程组的系 数列向量线性无关

第二节表上作业法 它的步骤可归纳为: (I)找出初始基可行解,即在m行n列产销平衡表上 给出m+n-1个数字格 (2)求各非基变量的检验数,即在表上计算空格的 检验数,并判别是否达到最优解,如果是最优 解,停止;否则转下一步 (3)确定换入变量和换出变量,找出新的基可行解, 在表上进行调整 (4)重复(2)(3),直至得到最优解 16
16 第二节 表上作业法 它的步骤可归纳为: (⑴)找出初始基可行解,即在m行n列产销平衡表上 给出m+n-1个数字格. (2) 求各非基变量的检验数,即在表上计算空格的 检验数,并判别是否达到最优解,如果是最优 解,停止;否则转下一步. (3) 确定换入变量和换出变量,找出新的基可行解, 在表上进行调整. (4) 重复(2)(3),直至得到最优解