
第六章运输问题 ◆第一节运输问题的数学模型 ◆第二节表上作业法 ◆第三节产销不平衡的运输问题 ◆第四节运输问题应用举例 2
2 第六章 运输问题 ◆第一节 运输问题的数学模型 ◆第二节 表上作业法 ◆第三节 产销不平衡的运输问题 ◆第四节 运输问题应用举例

◆ 在经济建设中,经常遇到大宗物资的调运问题, 如煤、钢材、粮食等.如果在我们考虑范围之内 有若干个生产基地和若干消费地点,根据已有的 交通网络,如何制定调运方案,使总的运费达到 最小,这就是运输问题, ·运输问题是特殊的线性规划问题,故可以用单纯 形法来求解,又因为它具有特殊性,因而它还具 有比单纯形法更为简便的解法,这就是我们专门 研究运输问题的目的。 第一节运输问题的数学模型 本节我们先引入运输问题的数学模型,然后讨论运输问题 数学模型的特点
3 n 在经济建设中,经常遇到大宗物资的调运问题, 如煤、钢材、粮食等. 如果在我们考虑范围之内 有若干个生产基地和若干消费地点,根据已有的 交通网络,如何制定调运方案,使总的运费达到 最小,这就是运输问题. n 运输问题是特殊的线性规划问题,故可以用单纯 形法来求解,又因为它具有特殊性,因而它还具 有比单纯形法更为简便的解法,这就是我们专门 研究运输问题的目的. 第一节 运输问题的数学模型 本节我们先引入运输问题的数学模型,然后讨论运输问题 数学模型的特点

运输问题的数学模型 例1假设有三家工厂,都将产品运往三个不同的商 店(如图),每家工厂每周的生产能力和每个商店每 周的需求量如表1和表2所示 表1 工 商店1 工 1 3 供应量(吨/周) 50 70 20 商店2 表2 商店 1 2 3 需求量(吨/周) 商店3 50 60 30 4
4 例1 假设有三家工厂,都将产品运往三个不同的商 店(如图),每家工厂每周的生产能力和每个商店每 周的需求量如表1和表2所示. 工厂1 工厂3 工厂2 商店1 商店3 商店2 表1 表2 工厂 1 2 3 供应量(吨/周) 50 70 20 商店 1 2 3 需求量(吨/周) 50 60 30 一 、 运输问题的数学模型
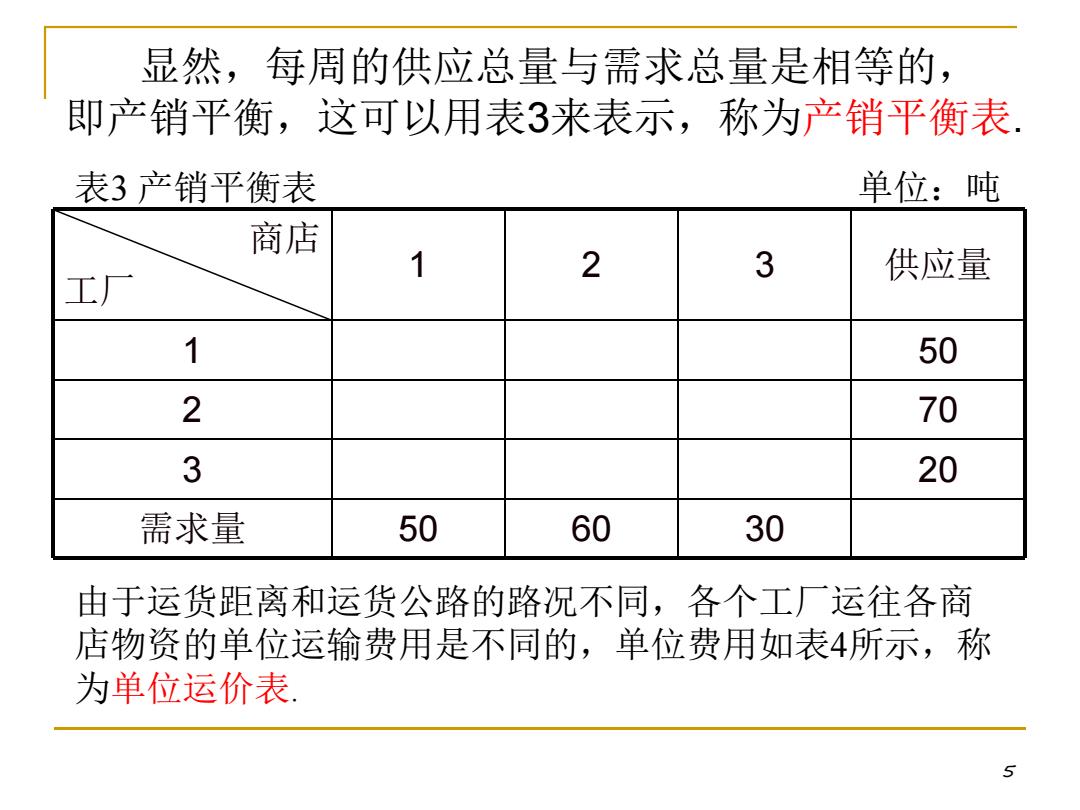
显然,每周的供应总量与需求总量是相等的, 即产销平衡,这可以用表3来表示,称为产销平衡表, 表3产销平衡表 单位:吨 商店 1 2 3 供应量 工厂 1 50 2 70 3 20 需求量 50 60 30 由于运货距离和运货公路的路况不同,各个工厂运往各商 店物资的单位运输费用是不同的,单位费用如表4所示,称 为单位运价表 5
5 显然,每周的供应总量与需求总量是相等的, 即产销平衡,这可以用表3来表示,称为产销平衡表. 由于运货距离和运货公路的路况不同,各个工厂运往各商 店物资的单位运输费用是不同的,单位费用如表4所示,称 为单位运价表. 表3 产销平衡表 单位:吨 商店 工厂 1 2 3 供应量 1 50 2 70 3 20 需求量 50 60 30
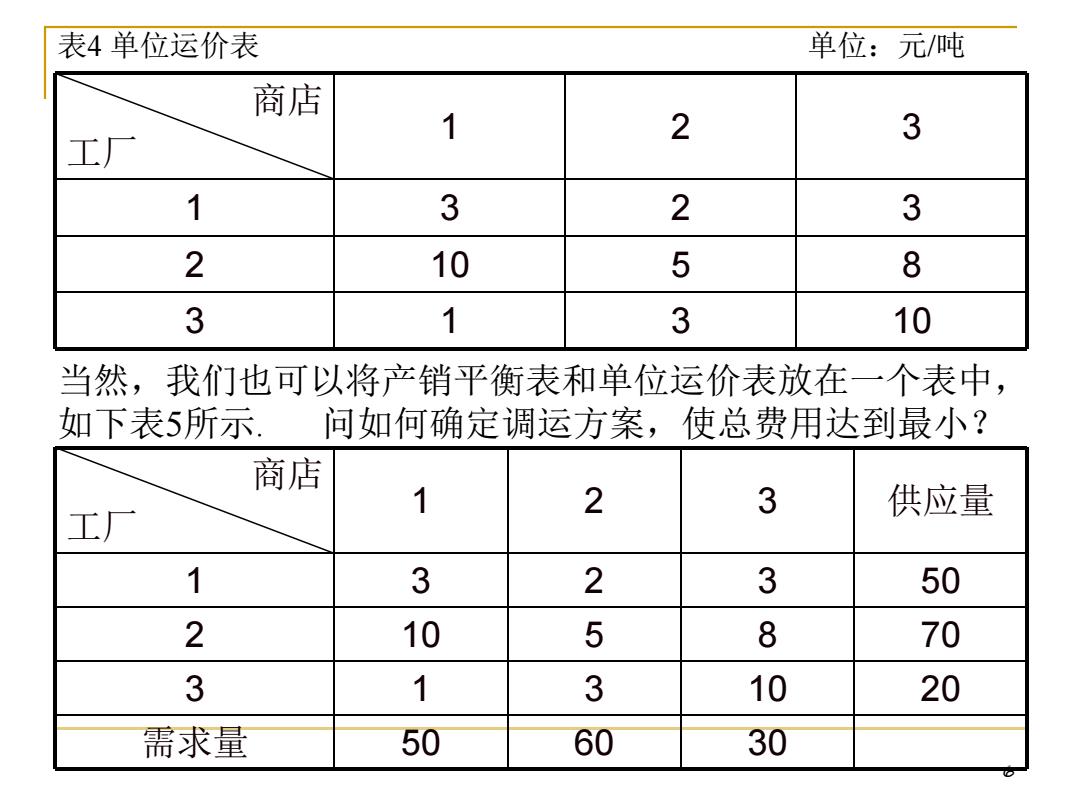
表4单位运价表 单位:元/吨 商店 2 3 工厂 1 3 2 3 2 10 5 8 3 1 3 10 当然,我们也可以将产销平衡表和单位运价表放在一个表中, 如下表5所示 问如何确定调运方案,使总费用达到最小? 商店 1 2 3 工厂 供应量 1 3 2 3 50 2 10 5 8 70 3 1 3 10 20 需求量 50 60 30
6 商店 工厂 1 2 3 供应量 1 3 2 3 50 2 10 5 8 70 3 1 3 10 20 需求量 50 60 30 商店 工厂 1 2 3 1 3 2 3 2 10 5 8 3 1 3 10 表4 单位运价表 单位:元/吨 当然,我们也可以将产销平衡表和单位运价表放在一个表中, 如下表5所示. 问如何确定调运方案,使总费用达到最小?