
发展历史 ,自动规划最初受自动推理证明很大的影响,用Situation Calculus的方式对初始状态、目标状态和行动做公理化描述, 使用归结定理证明来构造求解 然而,这种方式遇到框架问题的困难,从而引入对经典规划 的描述问题,其目的之一就是为框架问题提供一个简单的解 法 ·STRIPS假设:在效果中没提及的每个文字保持不变 ·STRIPS就是这方面早期的工作。这里介绍的经典表达 和STRIPS有同样的表达能力(STRIPS不同与自动定理证 明不同的是,将解的搜索和对系统的逻辑描述分离了) ~ADL权衡了一阶表达能力和推理的复杂性,之后扩展 的PDDL,为规划问题的标准描述语言 PDDL (The Planning Domain Definition Language)IPC (International Planning Competition两年一届)定义的标准 语言。已有一大批基于PDDL的通用规划器 STRIPS或PDDL方式与Situation Calculus方式都可以刻 画动态系统,两者在规划、预测方面的效果相同,但如果需 要更复杂的推理(如诊断),则只能使用Situation Calculus 2a0
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 发展历史 ▶ 自动规划最初受自动推理证明很大的影响,用 Situation Calculus 的方式对初始状态、目标状态和行动做公理化描述, 使用归结定理证明来构造求解 ▶ 然而,这种方式遇到框架问题的困难,从而引入对经典规划 的描述问题,其目的之一就是为框架问题提供一个简单的解 法: ▶ STRIPS 假设:在效果中没提及的每个文字保持不变 ▶ STRIPS 就是这方面早期的工作。这里介绍的经典表达 和 STRIPS 有同样的表达能力(STRIPS 不同与自动定理证 明不同的是,将解的搜索和对系统的逻辑描述分离了) ▶ ADL 权衡了一阶表达能力和推理的复杂性,之后扩展 的 PDDL,为规划问题的标准描述语言 ▶ PDDL (The Planning Domain Definition Language) 是由 IPC (International Planning Competition 两年一届) 定义的标准 语言。已有一大批基于 PDDL 的通用规划器 ▶ STRIPS 或 PDDL 方式与 Situation Calculus 方式都可以刻 画动态系统,两者在规划、预测方面的效果相同,但如果需 要更复杂的推理(如诊断),则只能使用 Situation Calculus

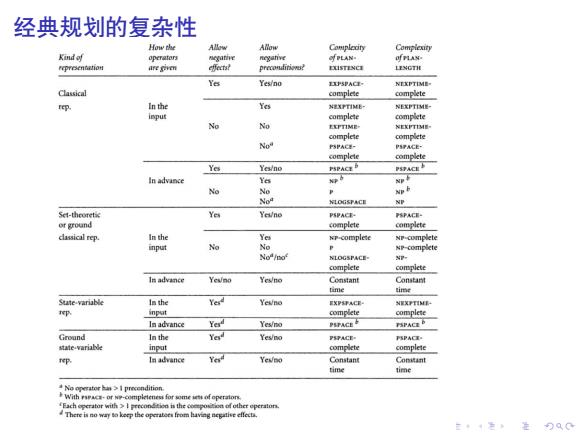
问题描述的计算复杂性 ·我们考虑在不同的问题描述下,经典规划存在解 (PLAN-EXT)和存在固定长度解(PLAN-LEN)问题的复杂 度。严格说来 PLAN-EXT={P|P是一个存在解的规划问题} PLAN-LEN={(P,n)|P是一个存在长度小于等于n的解的规划 ~经典规划问题有如下判定性结论: ·在不允许函数符号的情况下,PLAN-EXT和PLAN-LEN都 是可判定的。 在与允许函数符号的情况下,PLAN-EXT是半可判定的,而 PLAN-LEN是可判定的。 ~对于经典表达的经典规划问题,PLAN-EXT是 EXPSPACE-complete的,PLAN-LEN是 NEXPTIME-complete的。在表达中允许条件效果,并不会 增大复杂性
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 问题描述的计算复杂性 ▶ 我们考虑在不同的问题描述下,经典规划存在解 (PLAN-EXT) 和存在固定长度解 (PLAN-LEN) 问题的复杂 度。严格说来 PLAN-EXT = {P | P 是一个存在解的规划问题} PLAN-LEN = {(P, n) | P 是一个存在长度小于等于 n 的解的规划问题 } ▶ 经典规划问题有如下判定性结论: ▶ 在不允许函数符号的情况下,PLAN-EXT 和 PLAN-LEN 都 是可判定的。 ▶ 在与允许函数符号的情况下,PLAN-EXT 是半可判定的,而 PLAN-LEN 是可判定的。 ▶ 对于经典表达的经典规划问题,PLAN-EXT 是 EXPSPACE-complete 的,PLAN-LEN 是 NEXPTIME-complete 的。在表达中允许条件效果,并不会 增大复杂性
经典规划的复杂性 How the A品w Compleciry Compiexity Kind of operators neganve 号PLAN: 可1AM- are given DUISTINCI LENCTI Ye Yes/no EXPSPACE- Classical complete complete In the Ye NEXPTIMB- NEXPTIM是 input complete complete No a EKPTIME- NEXPTIME- complete complete No" 线PAC进- 伊PACE- complete complete Ye Yes/no PSPACE PSPACE In advance Ye NpF No No Np b No4 NLOGSPACE Set-theoretic Ye Yeno PSPACE- PSPACE- or ground complete complcte cassical rep. Inthe s NP-complete NP-complete input No No NP-complcte o/po NLOGSPACE- NP- complete compicte In advance Yevno Yesno Con时anl Constant time time State-variable In the e Yevno EXPSFACE- NEXFTIME- p input complete complete In advance Yerd Yes/no PSFACE 方PACE b Ground In the Yer Yesno PSPACE- TPA口 state-variable input complete complete p In advance Yesno Constant Conitant time np Each eperator with >I Frrcondtion is the coepostion of other eperators There is no way to keep the operatees from having nepative effect
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 经典规划的复杂性
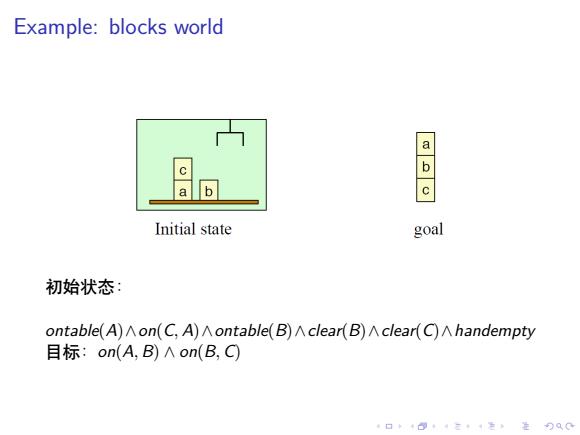
Example:blocks world c a b Initial state goal 初始状态: ontable(A)Aon(C,A)Aontable(B)Aclear(B)Aclear(C)^handempty 目标:on(A,B)Aon(B,C 口卡回t·三4色,是分Q0
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Example: blocks world 初始状态: ontable(A)∧on(C, A)∧ontable(B)∧clear(B)∧clear(C)∧handempty 目标:on(A, B) ∧ on(B, C)
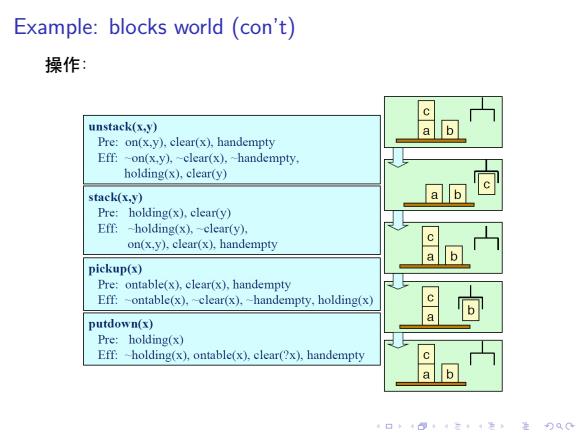
Example:blocks world (con't) 操作: unstack(x.y) Pre:on(x,y).clear(x),handempty Eff:-on(x.y),-clear(x).handempty, holding(x),clear(y) stack(x,y) Pre:holding(x).clear(y) Eff:-holding(x),-clear(y), on(x.y),clear(x),handempty pickup(x) Pre:ontable(x),clear(x),handempty Eff:-ontable(x),~clear(x).-handempty,holding(x) putdown(x) Pre:holding(x) Eff:-holding(x),ontable(x),clear(?x),handempty
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Example: blocks world (con’t) 操作: