电子科技大学：《光波导理论与技术 Optical Waveguides Principles and Technologies》课程教学资源（课件讲稿）第三章 条形光波导——结构与分析

University of Electronic Science and Technology of China 1.矩形波导的马卡悌里近似方法 956 口针对波导截面，建立图示坐标，根据之前的介绍，波导 内的模式可分为Ewmm与Dmn两种类型。 图3-3.分析矩形波导的理论模型 R R 基底 11

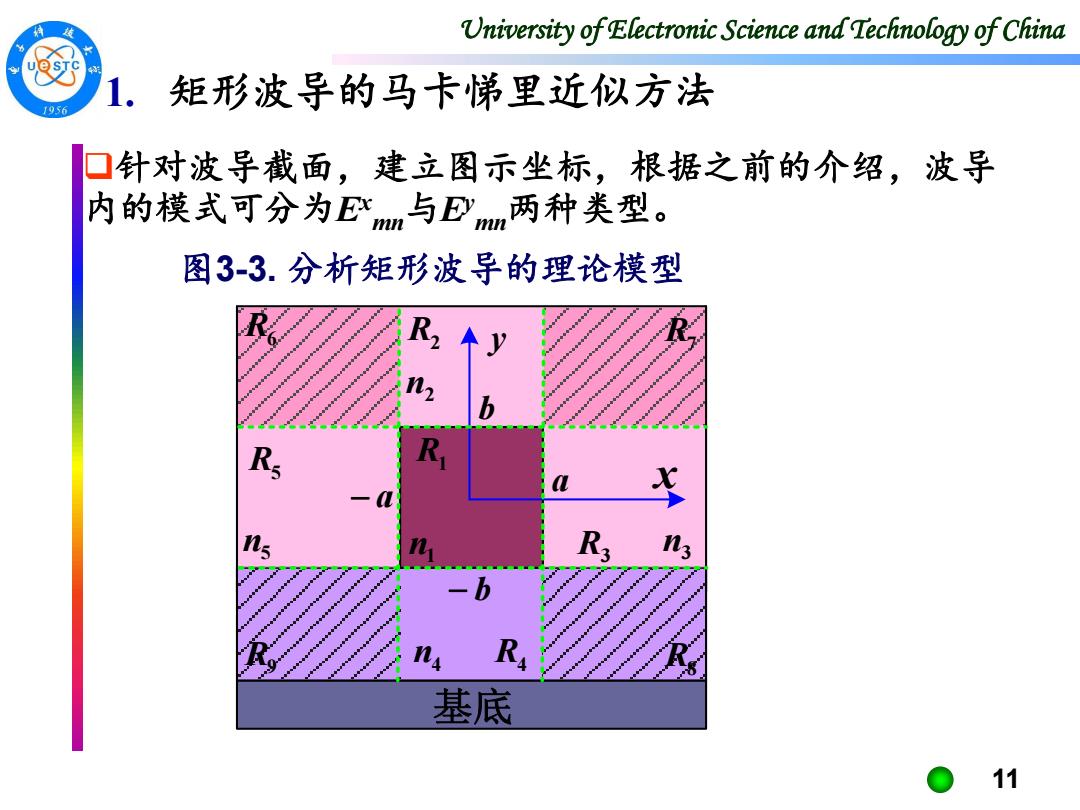
University of Electronic Science and Technology of China 11 图3-3. 分析矩形波导的理论模型 1. 矩形波导的马卡悌里近似方法 ❑针对波导截面，建立图示坐标，根据之前的介绍，波导 内的模式可分为Ex mn与Ey mn两种类型。 基底 n4 n5 n1 n3 n2 a x y − a − b b R2R1 R3 R4 R5 R6 R9 R8 R7

University of Electronic Science and Technology of China 1.矩形波导的马卡悌里近似方法 1956 Em模式 ① 导出场量满足的波动方程 该模式的偏振沿x方向，场量主要是E和H,故 E.≈0 (3-1) 此外，假定波导沿z方向均匀一致，因此 oloz=-jB (3-2) 波导内的场分布依然满足麦克斯韦方程 7×E=- 2=-jo4,H (3-3) V×i= aD =j086,E (3-4) 12

University of Electronic Science and Technology of China 12 x ➢ Emn 模式 1. 矩形波导的马卡悌里近似方法 j H t B E    = −  0    = − j E t D H r    =     = 该模式的偏振沿x方向，场量主要是Ex和Hy，故 Ey  0 此外，假定波导沿z方向均匀一致，因此  z = − j (3-1) (3-2) (3-3) (3-4) 波导内的场分布依然满足麦克斯韦方程 ① 导出场量满足的波动方程

University of Electronic Science and Technology of China 1.矩形波导的马卡悌里近似方法 956 展开以上两式并考虑到3-1及3-2式可得： -1 Hx= OE, (3-5) jot ay H, 1( jBE+ (3-6) jou H:= 1 OEs (3-7) jou ay H:jH,=j@ee,Ex (3-8) 13

University of Electronic Science and Technology of China 13 展开以上两式并考虑到3-1及3-2式可得： y E j H z x  −  = 0 1  ( ) 1 0 x E j E j H z y x   =  +   y E j H x z   = 0 1  y r x z j H j E y H +  =    (3-5) (3-6) (3-7) (3-8) 1. 矩形波导的马卡悌里近似方法

University of Electronic Science and Technology of China 1.矩形波导的马卡悌里近似方法 956 另一方面，因为 V·EE=0 (3-9) 也即是 8(e,E)-jie,E,=0 故有 E= 0(6,E.) 1 iBe,ax 1 1 Ex iBe,ax jB ox iB Ox (3-10) 这里假定 10e=0 E Ox (3-11) 也即是忽略了相对介电常数的方向依赖性。 14

University of Electronic Science and Technology of China 14 另一方面，因为   r E = 0 ( ) − = 0   r x r Ez E j x    (3-9) (3-10) 也即是 故有 x E x j E j E j x E j x E x x x r r r x r z   =   +   =   =         1 1 1 ( ) 1 这里假定 0 1 =   x r r   也即是忽略了相对介电常数的方向依赖性。 (3-11) 1. 矩形波导的马卡悌里近似方法

University of Electronic Science and Technology of China 1.矩形波导的马卡悌里近似方法 将3-10式代入3-5,3-6及3-7三式得 H气 1 02E. (3-12) oLB 8xay E) (3-13) 16 Ex H:=jow by (3-14) E.= Ex 1 iB ax (3-10) E =0 (3-1) 15

University of Electronic Science and Technology of China 15 1. 矩形波导的马卡悌里近似方法 y E j H x z   = 0 1  (3-12) (3-13) (3-14) x E j E x z   =  1 (3-10) Ey = 0 (3-1) 将3-10式代入3-5,3-6及3-7三式得 x y E H x x    = 2 0 1    ( ) 1 2 2 2 0 x E H E x y x   =  −   