8.2 目标物边界的描述 举例如下: (a)原始目标的区域 (b)逆时针旋转90°后的区域 原链码: ④212060 645 4 \/八/八/八八/八/\/八/八/八 归一化链码: 差分码: 6716626 6 17 Mg=0606454212 (c)旋转前 原链码:间43 42 020676 归一化差分码: /八/八/八八/八/\/八/八/八 M8=1662661767 差分码: 7166 2 d旋转后 Digital Image Processing 图8.2.2旋转前后的原链码及差分码
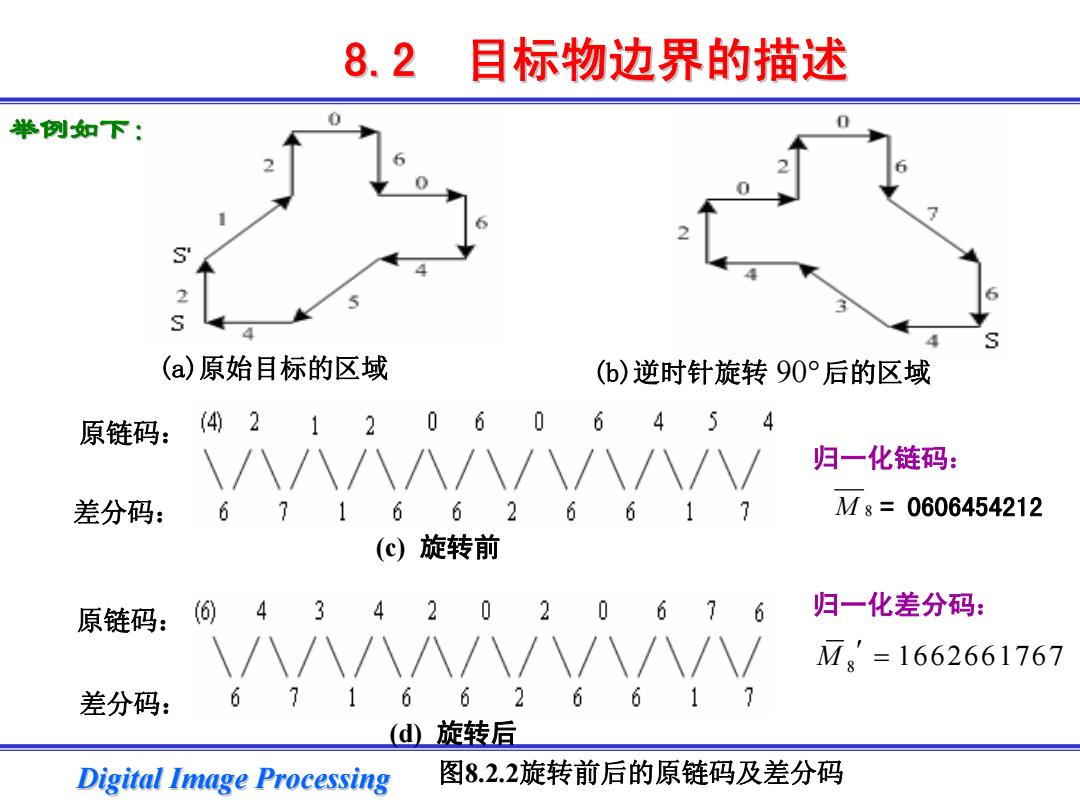
Digital Image Processing Digital Image Processing 举例如下: 8.2 目标物边界的描述 目标物边界的描述 (a)原始目标的区域 (b)逆时针旋转 后的区域 90° (c) 旋转前 原链码: 差分码: 差分码: 图8.2.2旋转前后的原链码及差分码 归一化链码: = 0606454212 归一化差分码: 原链码: (d) 旋转后 8 M ′ = 1662661767 M 8

8.2 目标物边界的描述 口目标物边界的链码表示 3.边界的形状数表示 由于归一化的差分码既具有唯一性,也具有目标物平移和 旋转不变性,因此可用来表示边界,称为形状数。形状数序 列的长度(位数)称为形状数的阶,它可作为闭合边界的周长。 如上图所示的目标边界,其 原链码为 M。=2120606454 差分码为 M8=6716626617, 形状数: M8′=1662661767, 形状数的阶为10。 Digital Image Processing
Digital Image Processing Digital Image Processing ◘目标物边界的链码表示 目标物边界的链码表示 3. 边界的形状数表示 边界的形状数表示 由于归一化的差分码既具有唯一性,也具有目标物平移和 由于归一化的差分码既具有唯一性,也具有目标物平移和 旋转不变性,因此可用来表示边界,称为形状数。形状数序 旋转不变性,因此可用来表示边界,称为形状数。形状数序 列的长度(位数)称为形状数的阶 称为形状数的阶,它可作为闭合边界的周长。 它可作为闭合边界的周长。 如上图所示的目标边界,其 如上图所示的目标边界,其 原链码为 , 差分码为 , 形状数: : , 形状数的阶为10。 8.2 目标物边界的描述 目标物边界的描述 8 M = 2120606454 8 M ′ = 6716626617 8 M ′ = 1662661767

8.2 目标物边界的描述 曲线拟合 曲线拟合以某种误差为标准。它是一种对曲线的近以表达形式,最后用 拟合曲线的参数来简洁描述原始曲线。这里介绍两种常用的拟合方法,即选 代拟合和最小均方误差拟合。 1.选代拟合:是利用选代的方法把曲线用分段线段近似表示出来。 首先用直线连接蜡点A和B,然后选取到直线AB距离最远的点C,如果点C偏 高AB超过了某种限度,则消去线段AB,然后分别连接AC和BC。根据迭代的 方法,对每段线段重复上述的步骤,直到偏离值小于原先设定的限度为 止,此时得到的折线就是对各边界点的选代拟合。 C6 B (a) (b) (c) 图8.2.3迭代拟合举例 Digital Image Processing
Digital Image Processing Digital Image Processing ◘曲线拟合 曲线拟合以某种误差为标准,它是一种对曲线的近似表达形式,最后用 拟合曲线的参数来简洁描述原始曲线。这里介绍两种常用的拟合方法,即迭 代拟合和最小均方误差拟合。 1.迭代拟合:是利用迭代的方法把曲线用分段线段近似表示出来。 首先用直线连接端点A和B,然后选取到直线AB距离最远的点C,如果点C偏 离AB超过了某种限度,则消去线段AB,然后分别连接AC和BC。根据迭代的 方法,对每段线段重复上述的步骤,直到偏离值小于原先设定的限度为 止,此时得到的折线就是对各边界点的迭代拟合。 8.2 目标物边界的描述 目标物边界的描述 (a) (b) (c) 图8.2.3 迭代拟合举例

8.2 目标物边界的描述 口曲线拟合 2.最小均方误差拟合 设由某图形的边界点组成的边界点集为 {《x,y),i=1,2,N, 我们试普用一条曲线近似拟合这个点集。根据最小均方误差的原则,要求该曲 线上各点和边界点集的“距离”最小,即使拟合的均方误差最小 8=立[y,-f(x,门 由于曲线y=f(X)经过边界点集上的所有点,其形式为 y=f(x)=co+cx+cx2+...+CyxM 用矩阵表示:y=XC,则每个点的误差列向量表示为:=y一XC 由此得出均方误差为:= 'e,可推出系数向量:c=[XIX][X7y] Digital Image Processing
Digital Image Processing Digital Image Processing ◘曲线拟合 2.最小均方误差拟合 设由某图形的边界点组成的边界点集为 , 我们试着用一条曲线近似拟合这个点集。根据最小均方误差的原则,要求该曲 线上各点和边界点集的“距离”最小,即使拟合的均方误差最小. 8.2 目标物边界的描述 目标物边界的描述 { } ( ) 1 2 i i x , y ,i , ,...,N = ( ) 1 2 N i i ε = − y fx N i =1 ⎡ ⎤ ∑ ⎣ ⎦ ( ) 2 01 2 M M y f x c c x c x ... c x = = + + ++ 用矩阵表示: ,则每个点的误差列向量表示为: 由此得出均方误差为: ,可推出系数向量: y Xc = 1 T T c XX Xy − = ⎡ ⎤⎡ ⎤ ⎣ ⎦⎣ ⎦ e 由于曲线y=f(x)经过边界点集上的所有点,其形式为 = y − Xc 1 T e e N ε ⎛ ⎞ = ⎜ ⎟ ⎝ ⎠
8.2 目标物边界的描述 曲线拟合 矩阵的表达形式如下: X Co 2 1 三 1 X3 yN 1 XN x民 x 若X为非奇异方阵时,可简化为:C=X-1y 然后通过对矩阵求逆及对包含多个未知数的线性方程组 求解,得到系数矩阵,就可确定拟合曲线的曲线方程。 Digital Image Processing
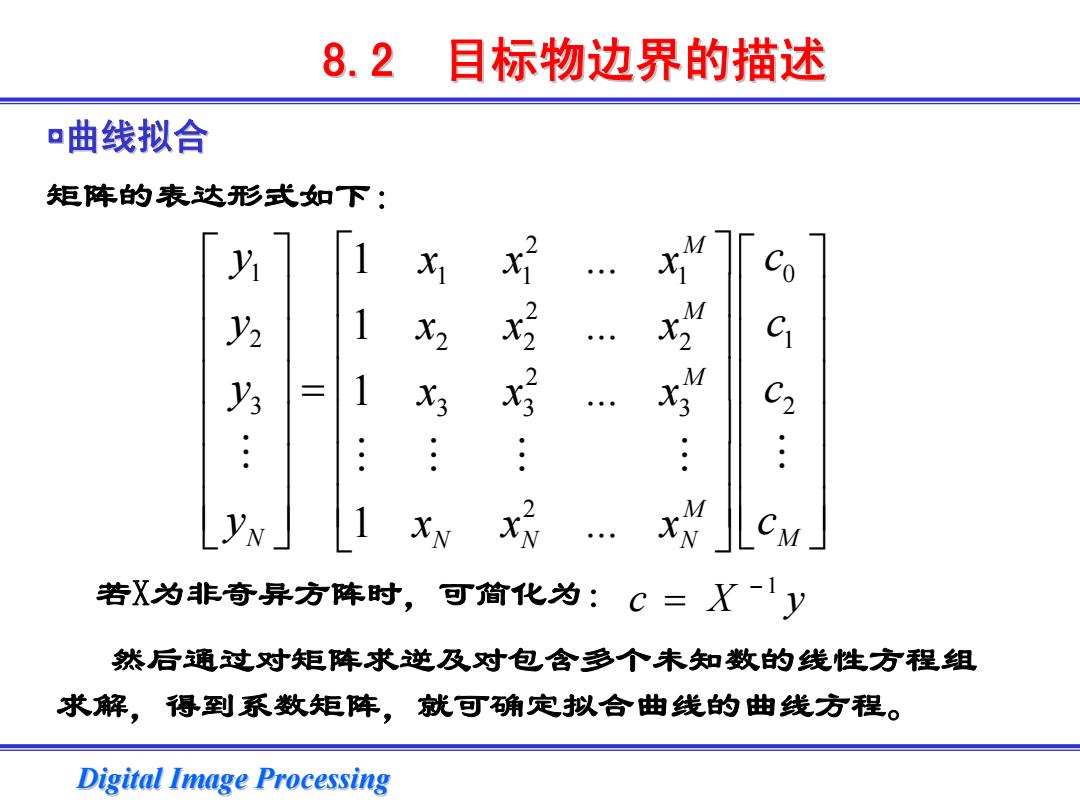
Digital Image Processing Digital Image Processing ◘曲线拟合 矩阵的表达形式如下: 2 1 11 1 0 2 2 22 2 1 2 3 33 3 2 2 1 1 1 1 M M M M N NN N M y x x ... x c y x x ... x c y x x ... x c y x x ... x c ⎡ ⎤ ⎡ ⎤⎡ ⎤ ⎢ ⎥ ⎢ ⎥⎢ ⎥ ⎢ ⎥ ⎢ ⎥⎢ ⎥ ⎢ ⎥ = ⎢ ⎥⎢ ⎥ ⎢ ⎥ ⎢ ⎥⎢ ⎥ ⎢ ⎥ ⎢ ⎥⎢ ⎥ ⎢ ⎥ ⎢ ⎥⎢ ⎥ ⎣ ⎦ ⎣ ⎦⎣ ⎦ # ## # # # 然后通过对矩阵求逆及对包含多个未知数的线性方程组 求解,得到系数矩阵,就可确定拟合曲线的曲线方程。 若X为非奇异方阵时,可简化为: 1 c X y − = 8.2 目标物边界的描述 目标物边界的描述