
8.1像素间的基本关系 距离测量 距离是描述像素间关系的基本参数,也是目标物几何特征和相似性的重要测度。 1.距离的定义 给定三个像素p(m1n1),q(m2n2),r(m3,n3),若D(p,q满足 (1)非负性:D(p,q)≥0,当且仅当p=q时,D(p,q)=0 (2)对称性:D(p,q)=D(q,p); (3)三角不等式:D(p,q)≤D(p,r)+D(r,q); 则D(p,q)称为距离的度量函数。 2.常用的三种距离 数字图像处理中,常用的距离度量有三种: (1) 欧几里德距离:D.(p,q)=V(m1-m2)2+(n1-n2)2 (2)街区距离: D4(p,q)=m1-m2|+|n,-n2| (3)棋盘距离: Ds(p,q)=max{m -m2 l,I n -n2 I Digital Image Processing
Digital Image Processing Digital Image Processing ◘距离测量 距离是描述像素间关系的基本参数,也是目标物几何特征和相似性的重要测度。 1.距离的定义 给定三个像素 ,若 满足 (1)非负性: ,当且仅当p=q时, ; (2)对称性: ; (3)三角不等式: ; 则 称为距离的度量函数。 2.常用的三种距离 数字图像处理中,常用的距离度量有三种: (1)欧几里德距离: (2)街区距离: (3)棋盘距离: 11 2 2 33 p(m ,n ),q(m ,n ),r(m ,n ) D(p,q) D(p,q) 0 ≥ D(p,q) =0 D (p ,q ) = D (q ,p ) D (p,q) D (p,r)+D (r,q) ≤ D(p,q) 2 2 D (p, q) (m -m ) (n -n ) e 1 = + 2 1 2 D (p, q) | m -m | | n n | 4 1 = 2 12 + − D (p,q) max | m m |,| n n | 8 1 = −− { 2 1 2 } 8.1 像素间的基本关系 像素间的基本关系
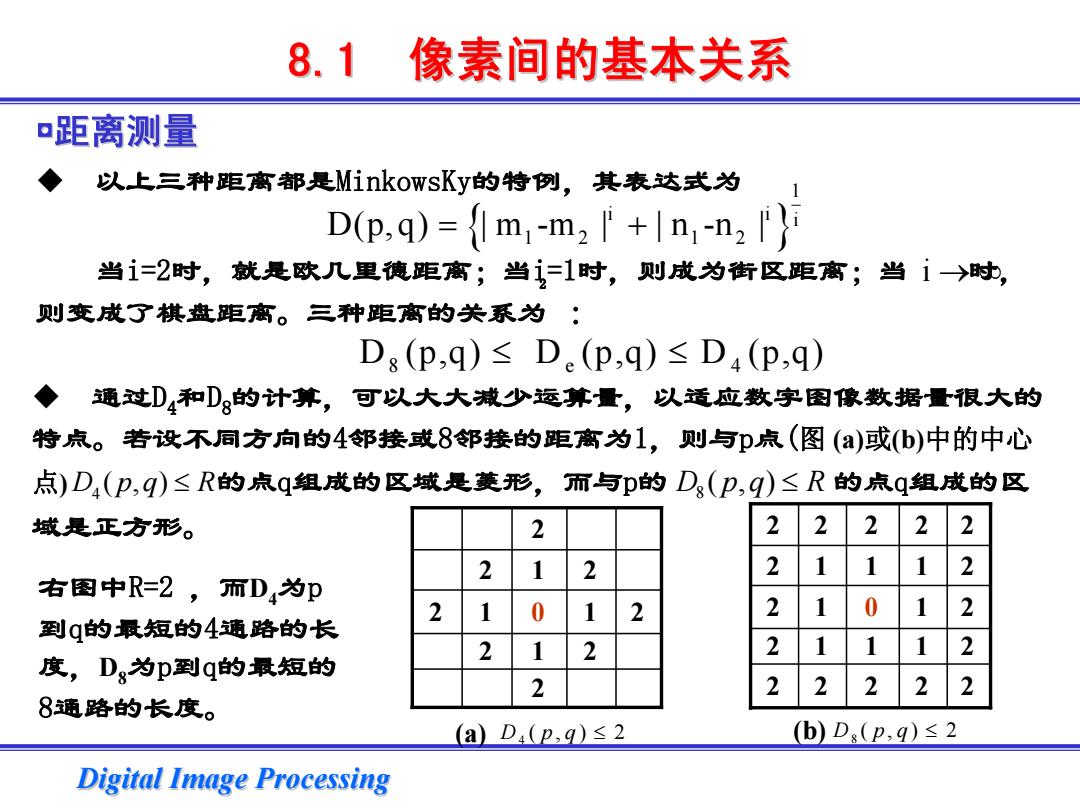
8.1像素间的基本关系 距离测量 以上三种距离都是MinkowsKy的特例,其表达式为 D(P.q)={lm:-m2 +n-n2 当i=2时,就是欧几里德距离;当=1时,则成为街区距离;当1→时, 则变成了棋盘距离。三种距离的关系为: Dg(p,q)≤De(p,q)≤D4(p,q) 通过D4和Dg的计算,可以大大减少远算量,以适应数字图像数据量很大的 特点。若设不同方向的4邻接或8邻接的距离为1,则与p点(图()或(b)中的中心 点)D,(p,q)≤R的点q组成的区域是菱形,而与D的Dg(p卫,q)≤R的点q组成的区 域是正方形。 2 2 2 2 2 2 右图中R=2,而D,为p 2 1 0 2 2 0 到q的最短的4通路的长 2 1 2 2 1 度,Dg为p到q的最短的 2 2 2 8通路的长度。 (a)D4(p,q)≤2 (b)Ds(p,q)≤2 Digital Image Processing
Digital Image Processing Digital Image Processing ◘距离测量 以上三种距离都是MinkowsKy的特例,其表达式为 当i=2时,就是欧几里德距离;当i=1时,则成为街区距离;当 时, 则变成了棋盘距离。三种距离的关系为 : { } 1 i i i D(p,q) 1 2 12 = + | m -m | | n -n | D (p,q) D (p,q) D (p,q) 8 e4 ≤ ≤ 通过D4和D8的计算,可以大大减少运算量,以适应数字图像数据量很大的 特点。若设不同方向的4邻接或8邻接的距离为1,则与p点(图 (a)或(b)中的中心 点) 的点q组成的区域是菱形,而与p的 的点q组成的区 域是正方形。 2 2 212 2 1 0 1 2 212 2 2 2 2 22 2 1 1 1 2 2 1 0 1 2 2 1 1 1 2 2 2 2 2 2 8.1 像素间的基本关系 像素间的基本关系 i → ∞ 4 D (,) pq R ≤ 8 D pq R (,) ≤ (a) (b) 4 D pq (,) 2 ≤ 8 D pq (,) 2 ≤ 右图中R=2 ,而D4为p 到q的最短的4通路的长 度,D8为p到q的最短的 8通路的长度

8.2 目标物边界的描述 图像中对于目标物形状的分析是图像检测和识别的关徒技术。所调边界描 述是将图像中目标物的边界作为图像的重要信息用简洁的数值序列表示出来。 ·目标物边界的链码表示 1.链码的定义 按照水平、垂直和两条对角线方向,可以为相邻的两个像素点定义4个方向 符:0、1、2、3,分别表示0°、90°、180°和270°四个方向。同样,也可以定义 8个方向符:0、1、2、3、4、5、6、7。链码就是用线段的起点加上由这几个 方向符所构成的一组数列,通常称之为Freeman链码。用Freeman链码表示曲线 时需要曲线的起点,对8链码而言,奇数码和偶数码的对应线段长度不等,规 定偶数码单位长度为1,奇数码的单位长度为√。 (a)四方向链码的方向符: (b)八方向链码的方向符。 Digital Image Processing
Digital Image Processing Digital Image Processing 8.2 目标物边界的描述 目标物边界的描述 图像中对于目标物形状的分析是图像检测和识别的关键技术。所谓边界描 述是将图像中目标物的边界作为图像的重要信息用简洁的数值序列表示出来。 ◘目标物边界的链码表示 目标物边界的链码表示 1. 链码的定义 按照水平、垂直和两条对角线方向,可以为相邻的两个像素点定义4个方向 符:0、1、2、3,分别表示0o、90o、180o和270o四个方向。同样,也可以定义 8个方向符:0、1、2、3、4、5、6、7。链码就是用线段的起点加上由这几个 方向符所构成的一组数列,通常称之为Freeman Freeman链码。用Freeman Freeman链码表示曲线 时需要曲线的起点,对8链码而言,奇数码和偶数码的对应线段长度不等,规 定偶数码单位长度为1,奇数码的单位长度为 2 。 0 3 1 2 0 1 2 3 4 5 6 7 (a)四方向链码的方向符; (b)八方向链码的方向符

8.2 目标物边界的描述 2.曲线的链码表示 (1)原链码从边界 (曲线)起点S开始,按顺时针方向观察每一线段走 向,并用相应的指向符表示,结果就形成表示该边界(曲线)的数码序列, 称为原链码,表示为 MN=SCa;=Saa2...an,a;=0,1,2,...,N-1 其中,S表示边界(曲线)的起点坐标,=4或8时分别表示四链码和八链码。: 当 边界(曲线)闭合时,会回到起点,S可省略。 (2) 归一化链码 原链码具有平移不变性(平移时不改变指向符),但当改变起点S时,会 得到不同的链码表示,即不具备唯一性。为此可引入归一化链码,其方法 是: 对于闭合边界,任选一起点$得到原链码,将链码看作由各方向数构成的 位自然数。将该码按一个方向循环。使其构成的位自然数最小,此时就形 成起点唯一的链码,称为归一化链码,也称为规格化链码。 Digital Image Processing
Digital Image Processing Digital Image Processing 2. 曲线的链码表示 (1)原链码 从边界(曲线)起点S开始,按顺时针方向观察每一线段走 向,并用相应的指向符表示,结果就形成表示该边界(曲线)的数码序列, 称为原链码,表示为 其中,S表示边界(曲线)的起点坐标,N=4或8时分别表示四链码和八链码。当 边界(曲线)闭合时,会回到起点,S可省略。 (2) 归一化链码 原链码具有平移不变性(平移时不改变指向符),但当改变起点S时,会 得到不同的链码表示,即不具备唯一性。为此可引入归一化链码,其方法 是: 对于闭合边界,任选一起点S得到原链码,将链码看作由各方向数构成的 n位自然数,将该码按一个方向循环,使其构成的n位自然数最小,此时就形 成起点唯一的链码,称为归一化链码,也称为规格化链码。 1 2 1 ... , 0,1, 2,..., 1 n N i ni i M S C a Sa a a a N = 8.2 目标物边界的描述 目标物边界的描述 = = =−

8.2 目标物边界的描述 (3) 差分码 归一化链码既具有平移不变性,也具备唯一性,但不具备旋转不变性。 对于四链码(或八链码),当目标物逆时针旋转90°(或45°)的倍时,其 原链码变为 n M N =( C a m i=l 其中4"=(a,+m))MODN,表示朱旋转前的指向苻加上m后对4(四链 码)或8(八链码)取模。一般 ☑,≠®m举例见图8.2.2所示,旋转前 后的原链码确实不同。 为了得到具有旋转不变性的链码,我们可定义所谓的差分码。链码对应 的差分码定义为: M=C.a,a=(a-a)MOD N a=(a-a)MOD N,i=2,3..n i- (4) 归一化的差分码 对差分码进行(起点)归一化,就可得到归一化(唯一)的差分码, 它具有平移和旋转不变性。也具有唯一性。 Digital Image Processing
Digital Image Processing Digital Image Processing (3) 差分码 归一化链码既具有平移不变性,也具备唯一性,但不具备旋转不变性。 对于四链码(或八链码),当目标物逆时针旋转90o(或45o)的m倍时,其 原链码变为 其中 ,表示未旋转前的指向符加上m后对4(四链 码)或8(八链码)取模。一般 。举例见图8.2.2所示,旋转前 后的原链码确实不同。 为了得到具有旋转不变性的链码,我们可定义所谓的差分码。链码对应 的差分码定义为: , , 1 n m N i i 8.2 目标物边界的描述 目标物边界的描述 M C a = = 1 n N i i M C a = ′ ′ = 1 1 ( )n a a a MOD N ′ = − 1 ( ) , 2,3,..., i ii a a a MOD N i n − ′ =− = ( ) mi i a a m MOD N = + m i i a a (4) 归一化的差分码 对差分码进行(起点)归一化,就可得到归一化(唯一)的差分码, 它具有平移和旋转不变性,也具有唯一性。 ≠