
y(t)=y(to)+y'(to)(t-to)+ y"(c1)(t-to)2 2 Wheny(to)to(t)and ht are substituted in the equation aboved,the result is an expression for y(): h2 y(t)=y(to)+hf(to.y(to))+y"(c1) If the step size h is chosen small enough,then we may neglect the second-order term(involving h2)and get y=yo+hf(to-Yo), which is Euler's approximation. The purpose is repeated and generates a sequence of points that approximates the solution curve y=y(t).The general step for Euler's method is %=y(60)2 y=y+hf(t:y),for k=0,1,...,M-1
0 0 1 ( ), ( , ), for 0,1, , 1. k k k k y y t y y hf t y k M + = = + = −
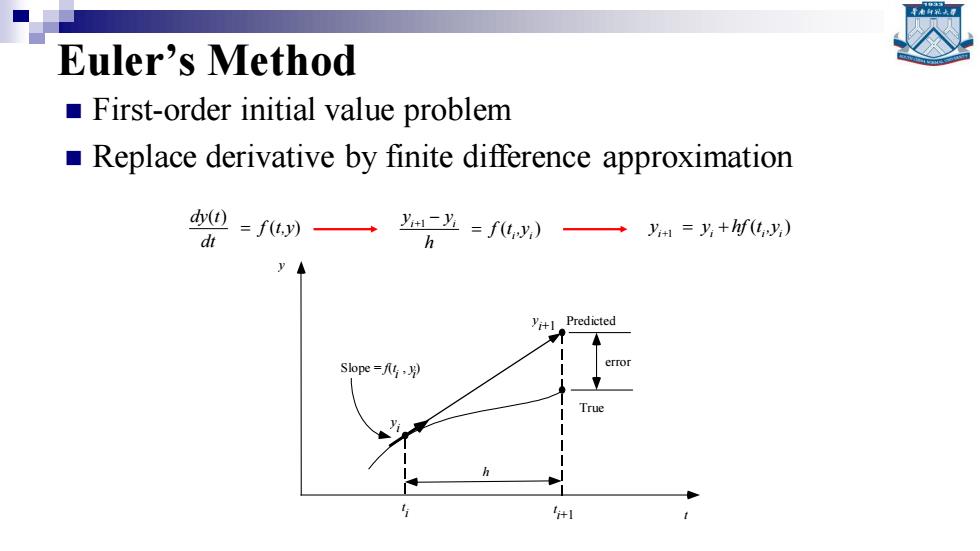
Euler's Method First-order initial value problem Replace derivative by finite difference approximation 0=fu一-=fy) d =i+hf(ty) h +1 Predicted Slope=4,月 error True
Euler’s Method ◼ First-order initial value problem ◼ Replace derivative by finite difference approximation y i y i+1 h t i+1 t i t y Predicted True error Slope = f(t i , y i ) ( ) ( ) f t,y dt dy t = ( ) 1 i i i+ i f t ,y h y y = − ( ) i+1 i i i y = y + hf t ,y