
§4≈2 概率分布 (probability distribuution) 随机变量(random variable) 作一次试验,其结果有多种可能。每 一种可能结果都可用一个数来表示,把 这些数作为变量的取值范围,则试验结 果可用变量来表示
§4~2 概率分布 (probability distribuution) ⚫ 一、随机变量(random variable) ⚫ 作一次试验,其结果有多种可能。每 一种可能结果都可用一个数来表示,把 这些数作为变量的取值范围,则试验结 果可用变量来表示

随机变量(random variable) ·1、离散型随机变量 discrete random variable) 。2、连续型随机变量 (continuous random variable
随机变量(random variable) ⚫ 1、离散型随机变量 ⚫(discrete random variable) ⚫ 2、连续型随机变量 ⚫(continuous random variable )

§4~3正态分布 normal distribution (高斯分布)
§4~3 正态分布 normal distribution (高斯分布)

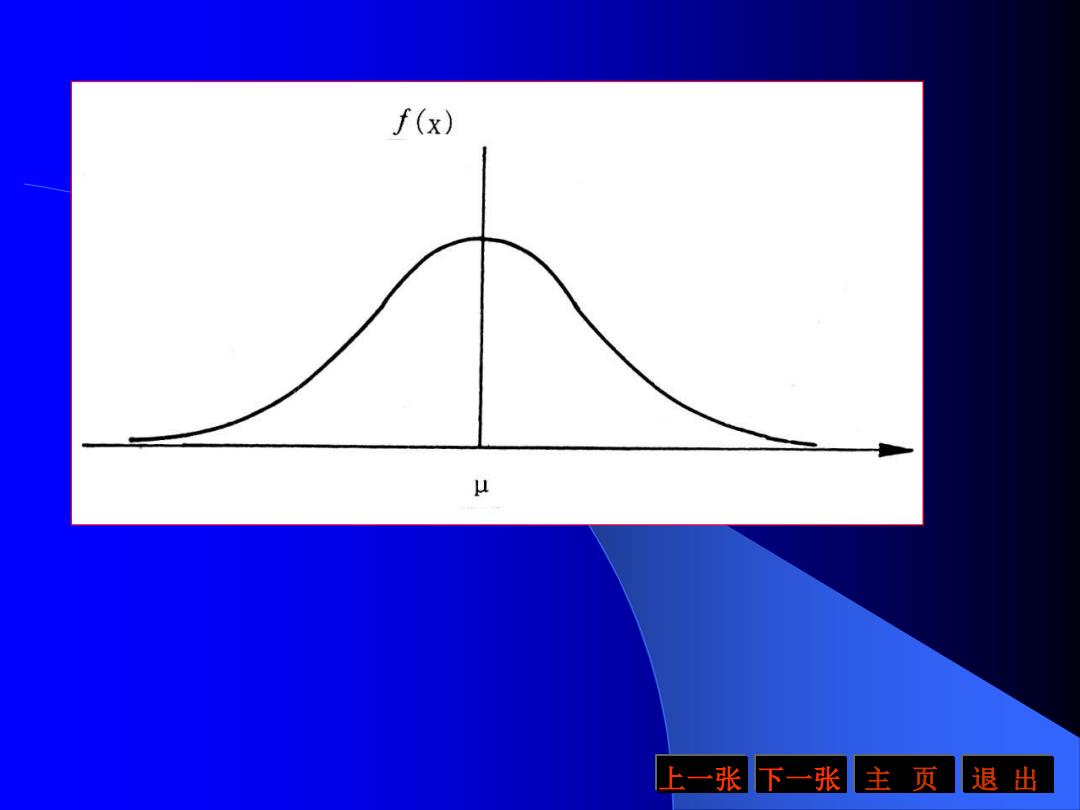
一、正态分布的定义及其特征 (一)正态分布的定义若连续型随机变量x 的概率分布密度函数为 (x-)2 f(x)= (4-6 其中为平均数,σ为方差,则称随机变量x 服从正态分布,记为x一N(u,σ)。相应的概率分 布函数为 ) rw)-a2元 e dx (4-7) 上一张下一张主页 退出
一、正态分布的定义及其特征 (一) 正态分布的定义 若连续型随机变量x 的概率分布密度函数为 (4-6) 其中μ为平均数,σ 2为方差,则称随机变量x 服从正态分布,记为x~N(μ,σ2 )。相应的概率分 布函数为 (4-7) 2 2 2 ( ) 2 1 ( ) − − = x f x e − − − = x x F x e dx 2 2 2 ( ) 2 1 ( ) 上一张 下一张 主 页 退 出
f(x) μ 上一张下一张主页退出
分布密度曲线如图4—2所示。 上一张 下一张 主 页 退 出