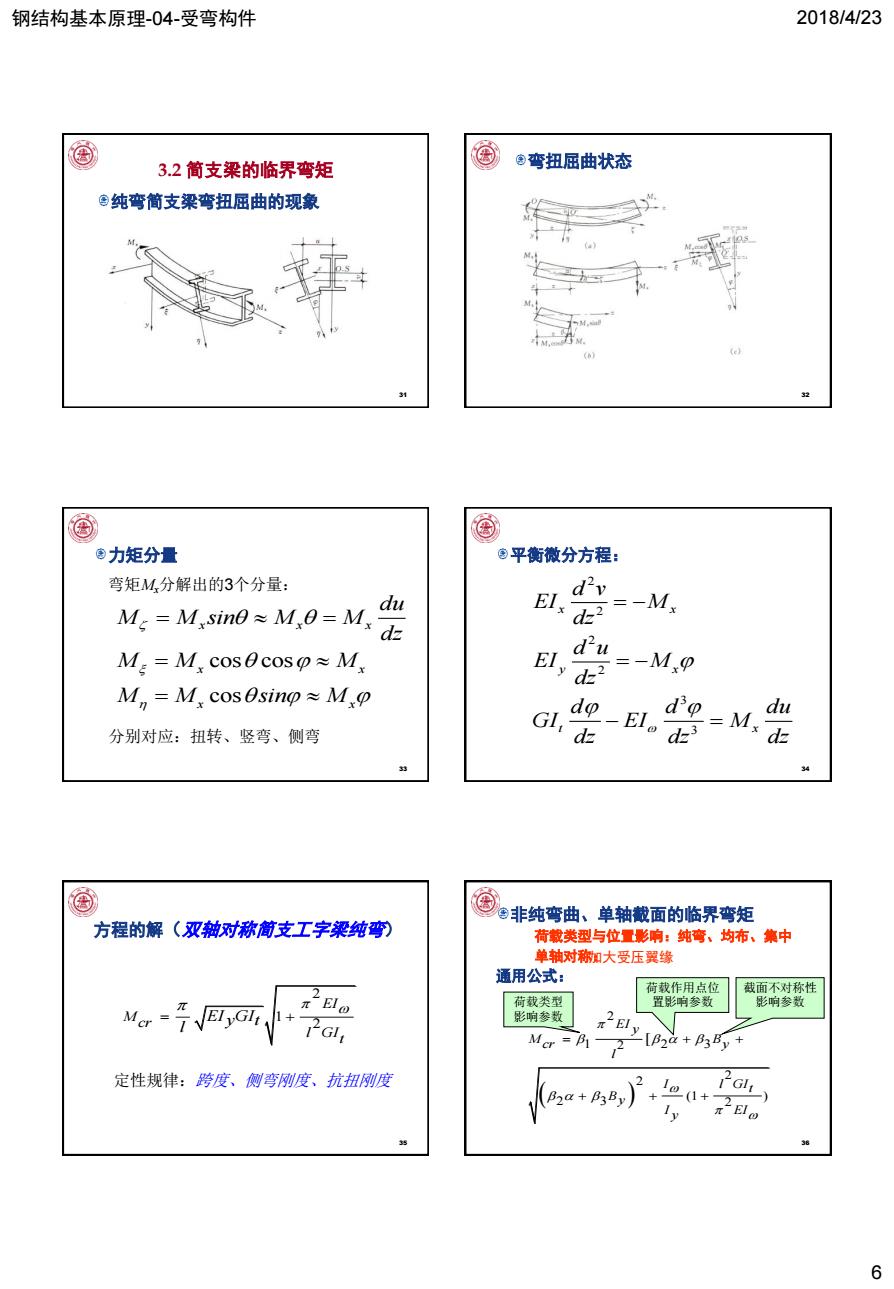
钢结构基本原理-04-受弯构件 2018/4/23 3.2简支梁的临界弯矩 粤弯扭屈曲状态 ©纯弯简支梁弯扭屈曲的现象 ®力矩分量 ©平衡微分方程: 弯矩M分解出的3个分量: dv M,=M,simb≈M,0=M,d正 du 2=-M M:=M,cos0coso≈Mx du de? --M.P M,=M,cos0sinp≈Mxp do do =M, du 分别对应:扭转、竖弯、侧弯 Gl:d dz 34 国 ©非纯弯曲、单轴戴面的临界弯矩 方程的解(双轴对称简支工字梁纯弯 荷载类型与位量影响:纯弯、均布、集中 单轴对称知大受压翼缘 通用公式: 荷载作用点位 截面不对称性 πElo 荷载类型 置影响参数 影响参数 影响参数 12GI Mcr =B 子+ 定性规律:跨度、侧弯刚度、抗扭刚度 B2a+B3By 19 6
钢结构基本原理-04-受弯构件 2018/4/23 6 31 3.2 简支梁的临界弯矩 纯弯简支梁弯扭屈曲的现象 32 弯扭屈曲状态 33 力矩分量 cos cos cos x x x x x x x du M M sin M M dz M M M M M sin M 弯矩Mx分解出的3个分量: 分别对应:扭转、竖弯、侧弯 34 平衡微分方程: 2 2 2 2 3 3 x x y x t x d v EI M dz d u EI M dz d d du GI EI M dz dz dz 35 方程的解(双轴对称简支工字梁纯弯) 2 1 2 EI Mcr l GIt EI GI y t l 定性规律:跨度、侧弯刚度、抗扭刚度 36 非纯弯曲、单轴截面的临界弯矩 荷载类型与位置影响:纯弯、均布、集中 单轴对称: 通用公式: 2 1 2 3 2 2 2 (1 ) 2 3 2 [ EI y M B cr y l I l GIt By I EI y 荷载作用点位 置影响参数 截面不对称性 荷载类型 影响参数 影响参数 加大受压翼缘

钢结构基本原理-04-受弯构件 2018/4/23 国 3.3整体稳定系数 国 3.3.1双轴对称工字梁、纯弯 Ocr= πEI W Mcr= →simplified 10.17×105 2 1+ 元y1 10.17×105 那 4.4h Ah + 4.4h 17 国 定义稳定系数 p。-cg 稳定系数表达式 ocr P= 稳定要求:M≤M.oro≤ocr f, M≤c-0,=,f 4320Ah (元y1 2 235 Design:= ● Wx YR YR w. 1+ 4.4h Mx≤∫ PW 3.3.2工字梁一般情况稳定系数表达式 ©工字梁一般情况稳定系数表达式 非纯弯、单轴对称一简化 荷载情况:纯弯与非纯弯 一般情况稳定系数表达式: 4320Ah 截面情况:单、双轴对称 P6=B。 弹塑性影响:应予考虑 诏所 元yl +nb 235 4.4h 42 7
钢结构基本原理-04-受弯构件 2018/4/23 7 37 3.3 整体稳定系数 3.3.1 双轴对称工字梁、纯弯 2 2 2 2 EI y I l GIt Mcr l I EI y y simplified 5 2 1 2 4.4 10.17 10 1 y Mcr t y Ah h 38 1 5 2 10.17 10 1 2 4.4 cr x x M cr W yt Ah W h y 39 Design = x b y b x R R x b x M f cr f W M f W : 定义稳定系数 b y cr f 稳定要求: cr or M M x cr 40 稳定系数表达式 1 2 4320 1 2 4.4 b y x cr f Ah yt W h y 235 y f 41 3.3.2 工字梁一般情况稳定系数表达式 荷载情况:纯弯与非纯弯 截面情况:单、双轴对称 弹塑性影响:应予考虑 42 工字梁一般情况稳定系数表达式 1 4320 2 2 235 1 4.4 b b x b y Ah W y yt h f 非纯弯、单轴对称→简化 一般情况稳定系数表达式: