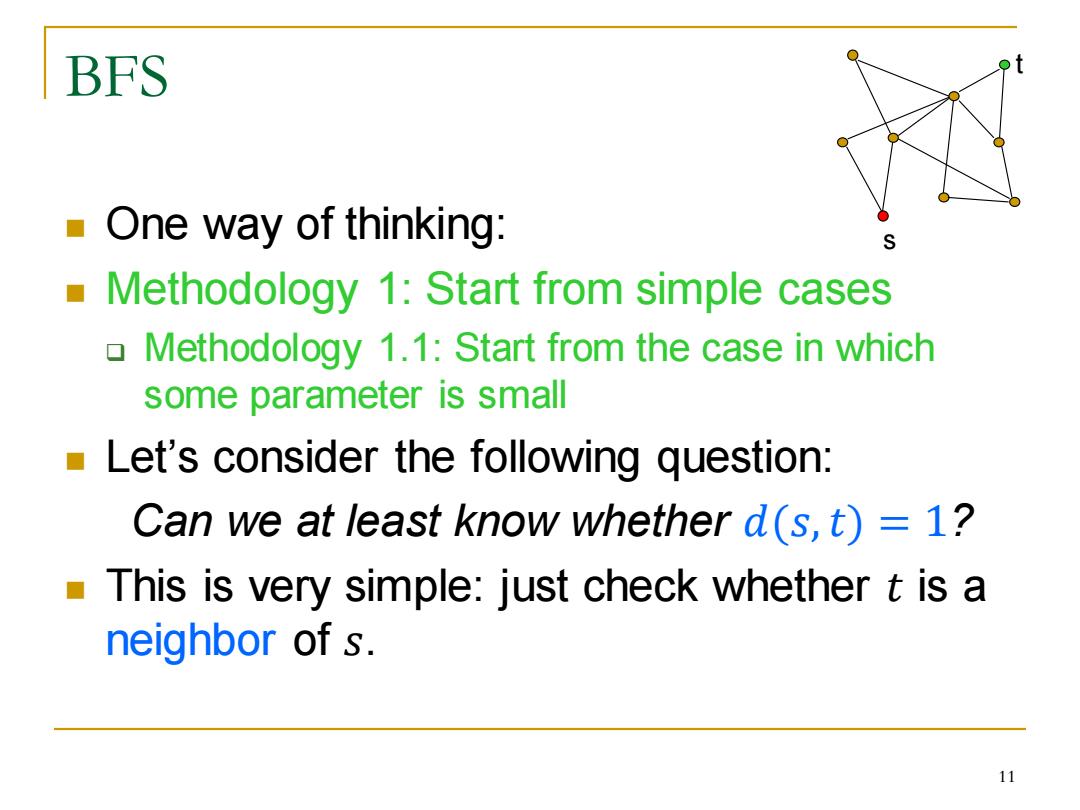
BFS One way of thinking: S ■ Methodology 1:Start from simple cases 0 Methodology 1.1:Start from the case in which some parameter is small Let's consider the following question: Can we at least know whether d(s,t)=1? This is very simple:just check whether t is a neighbor of s. 11
BFS ◼ One way of thinking: ◼ Methodology 1: Start from simple cases ❑ Methodology 1.1: Start from the case in which some parameter is small ◼ Let’s consider the following question: Can we at least know whether 𝑑(𝑠,𝑡) = 1? ◼ This is very simple: just check whether 𝑡 is a neighbor of 𝑠. s t 11
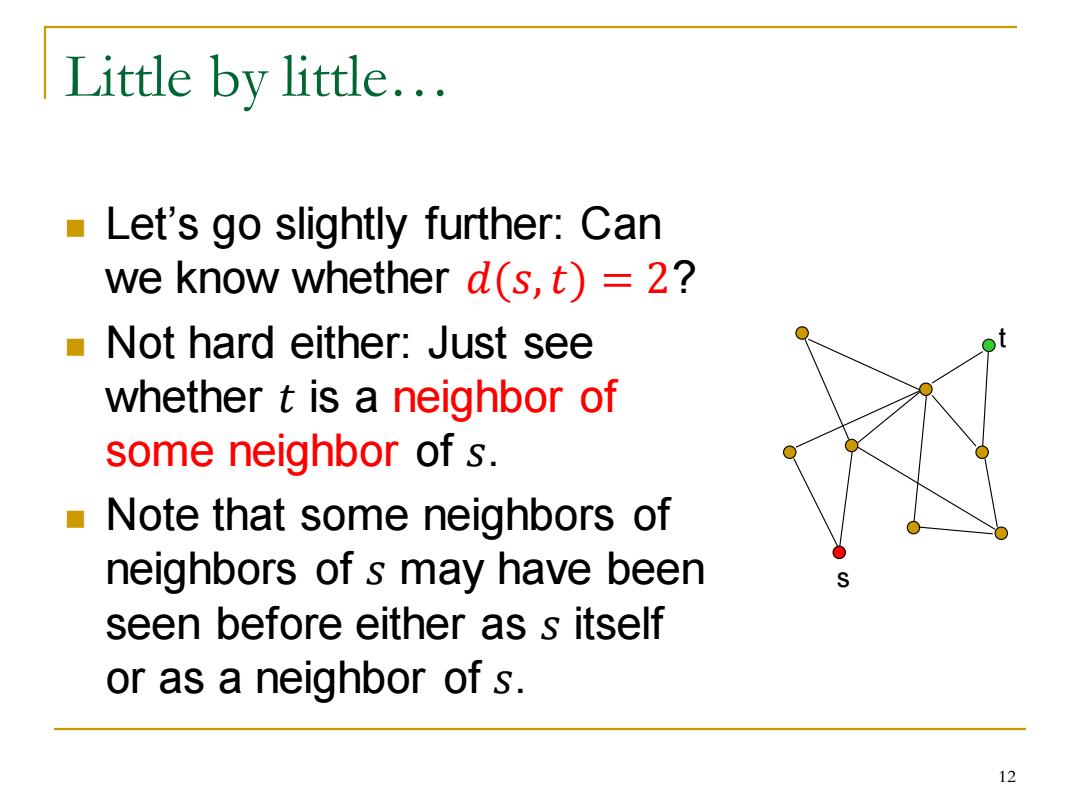
Little by little... Let's go slightly further:Can we know whether d(s,t)=2? Not hard either:Just see whether t is a neighbor of some neighbor of s. Note that some neighbors of neighbors of s may have been seen before either as s itself or as a neighbor of s. 12
Little by little… ◼ Let’s go slightly further: Can we know whether 𝑑(𝑠,𝑡) = 2? ◼ Not hard either: Just see whether 𝑡 is a neighbor of some neighbor of 𝑠. ◼ Note that some neighbors of neighbors of 𝑠 may have been seen before either as 𝑠 itself or as a neighbor of 𝑠. s t 12

In general? Ni(s)=fall neighbors of s} a the vertices with distance 1 from s. N2(s)={all neighbors of N(s)}-N(s)-{s} the vertices with distance 2 from s. N3(s)={all neighbors of N2(s)}-N2(s)-N(s)-{s} the vertices with distance 3 from s. Ni(s)={all neighbors of Ni-1(s)}-Ni-1(s)-...- N1(S)-{S} If we find t in this step i,then d(s,t)=i. 13
In general? ◼ 𝑁1(𝑠) = {all neighbors of 𝑠} ❑ the vertices with distance 1 from 𝑠. ◼ 𝑁2(𝑠) = {all neighbors of 𝑁1(𝑠)} − 𝑁1 𝑠 − {𝑠} ❑ the vertices with distance 2 from 𝑠. ◼ 𝑁3(𝑠) = {all neighbors of 𝑁2(𝑠)} − 𝑁2(𝑠) − 𝑁1(𝑠) − {𝑠} ❑ the vertices with distance 3 from 𝑠. ◼ … ◼ 𝑁𝑖(𝑠) = {all neighbors of 𝑁𝑖−1(𝑠)} − 𝑁𝑖−1(𝑠) − ⋯ − 𝑁1(𝑠) − {𝑠} ◼ If we find 𝑡 in this step 𝑖, then 𝑑(𝑠,𝑡) = 𝑖. s t 13

BFS This is called the breadth-first search(BFS). ■Why it works? [Thm]If we find t in Step k,then d(s,t)=k. Or equivalently, [Thm]Ni(s)contains exactly those vertices with distance k from s. 14
BFS ◼ This is called the breadth-first search (BFS). ◼ Why it works? ◼ [Thm] If we find 𝑡 in Step 𝑘, then 𝑑(𝑠,𝑡) = 𝑘. Or equivalently, ◼ [Thm] 𝑁𝑘(𝑠) contains exactly those vertices with distance 𝑘 from 𝑠. 14

Proof of Nk(s)={v:d(v,s)=k} Let's prove this by induction on k. k =1:trivially true. 2 0飞 Suppose k is correct, consider k+1.Need: 1.If d(s,t)=k +1,then t E Nk+1(s) ▣2.Ift∈Nk+1(s),then d(S,t)=k+1 15
Proof of 𝑁𝑘(𝑠) = {𝑣: 𝑑(𝑣, 𝑠) = 𝑘} ◼ Let’s prove this by induction on 𝑘. ◼ 𝑘 = 1: trivially true. ◼ Suppose 𝑘 is correct, consider 𝑘 + 1. Need: ❑ 1. If 𝑑(𝑠,𝑡) = 𝑘 + 1, then 𝑡 ∈ 𝑁𝑘+1(𝑠) ❑ 2. If 𝑡 ∈ 𝑁𝑘+1(𝑠), then 𝑑(𝑠,𝑡) = 𝑘 + 1 s 1 2 k t 15