
CSC3160: Design and Analysis of Algorithms Week 8: Maximum Network Flow Instructor: Shengyu Zhang 1
Instructor: Shengyu Zhang 1
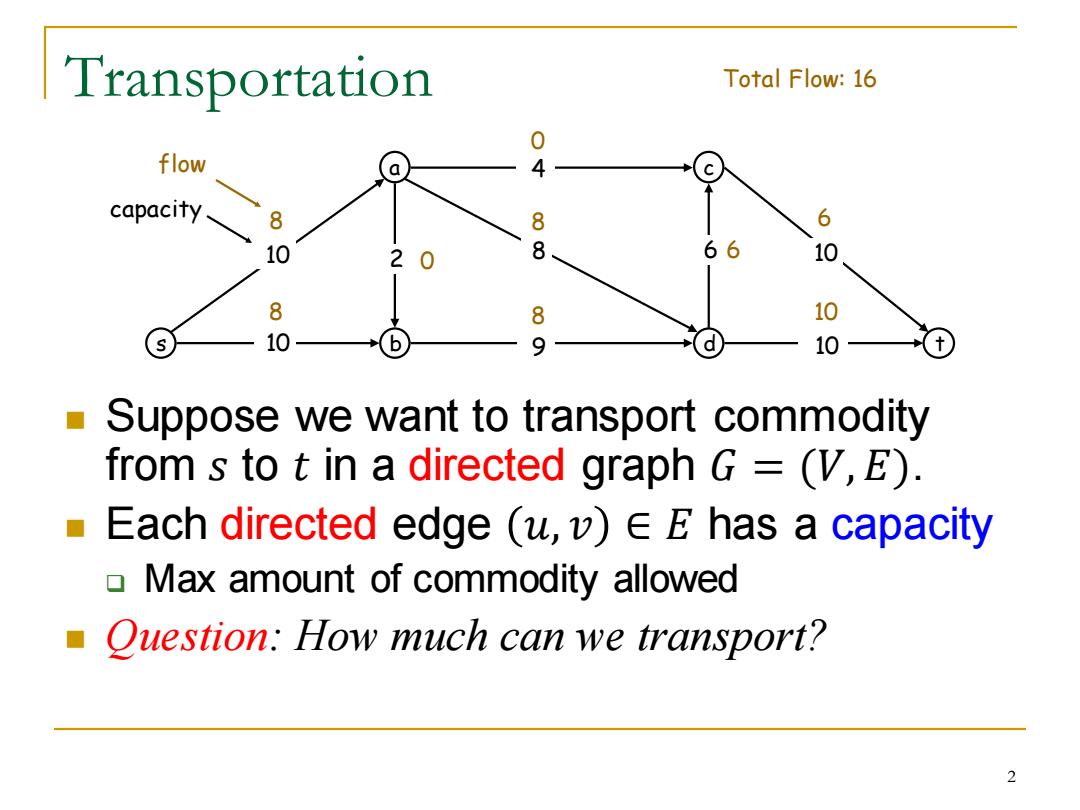
Transportation Total Flow:16 0 flow a 4 capacity 8 8 6 10 2 0 8 66 10 8 8 10 10 9 10 Suppose we want to transport commodity from s to t in a directed graph G=(V,E). Each directed edge (u,v)EE has a capacity Max amount of commodity allowed Question:How much can we transport? 2
Transportation ◼ Suppose we want to transport commodity from 𝑠 to 𝑡 in a directed graph 𝐺 = (𝑉, 𝐸). ◼ Each directed edge 𝑢, 𝑣 ∈ 𝐸 has a capacity ❑ Max amount of commodity allowed ◼ Question: How much can we transport? s a b c 10 d t 10 9 8 4 10 2 6 10 8 0 6 8 8 10 8 0 6 flow Total Flow: 16 capacity 2
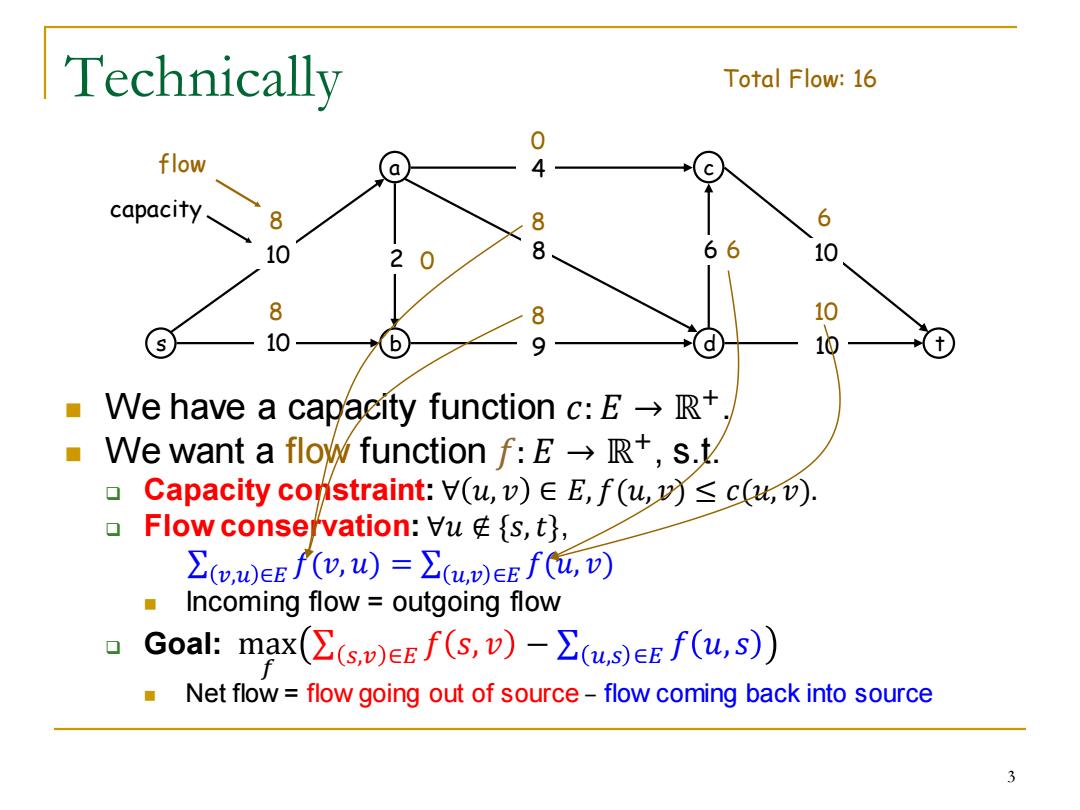
Technically Total Flow:16 0 flow 4 capacity 8 88 6 10 2 6 10 8 8 10 10 9 We have a capacity function c:ER+ We want a flow function f:ER+,s.t. 0 Capacity constraint:V(u,v)EE,f(u,v)<c(u,v). 口 Flow consefvation:Vus,t}, L(o0EEf,W)=∑(uEEf(u可 Incoming flow outgoing flow Goal:max((s)eEf(s,v)-(us)eEf(u,s)) Net flowflow going out of source-flow coming back into source 3
Technically ◼ We have a capacity function 𝑐: 𝐸 → ℝ +. ◼ We want a flow function 𝑓: 𝐸 → ℝ + , s.t. ❑ Capacity constraint: ∀ 𝑢, 𝑣 ∈ 𝐸, 𝑓(𝑢, 𝑣) ≤ 𝑐(𝑢, 𝑣). ❑ Flow conservation: ∀𝑢 ∉ {𝑠,𝑡}, σ 𝑣,𝑢 ∈𝐸 𝑓(𝑣, 𝑢) = σ 𝑢,𝑣 ∈𝐸 𝑓(𝑢, 𝑣) ◼ Incoming flow = outgoing flow ❑ Goal: max 𝑓 σ 𝑠,𝑣 ∈𝐸 𝑓 𝑠, 𝑣 − σ 𝑢,𝑠 ∈𝐸 𝑓 𝑢, 𝑠 ◼ Net flow = flow going out of source – flow coming back into source s a b c 10 d t 10 9 8 4 10 2 6 10 8 0 6 8 8 10 8 0 6 flow Total Flow: 16 capacity 3
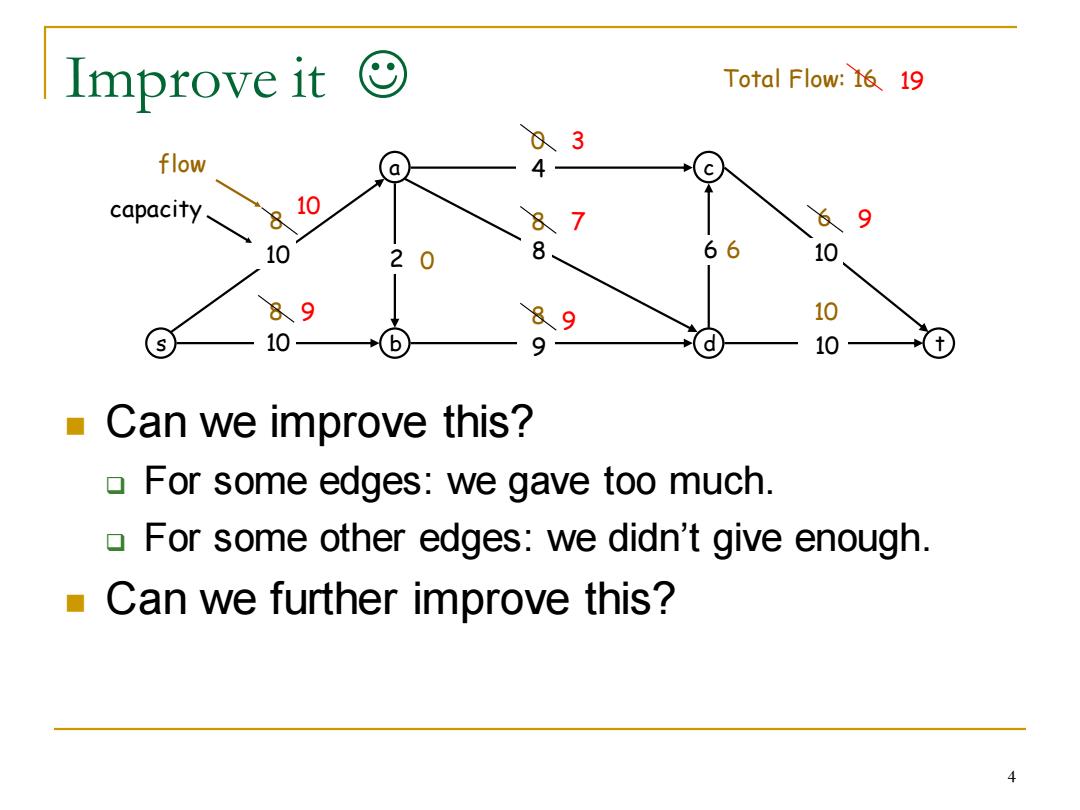
Improve it Total Flow:16 19 03 flow a 4 capacity 10 8 87 9 10 2 0 8 66 10 89 89 10 10 b 9 d 10 Can we improve this? For some edges:we gave too much. For some other edges:we didn't give enough Can we further improve this? 4
Improve it ☺ ◼ Can we improve this? ❑ For some edges: we gave too much. ❑ For some other edges: we didn’t give enough. ◼ Can we further improve this? s a b c 10 d t 10 9 8 4 10 2 6 10 8 0 6 8 8 10 8 0 6 flow Total Flow: 16 capacity 7 9 3 10 9 9 19 4

Network Flow Can you give a good algorithm? Methodology 5:Approach to the optimum by a sequence of improvements. 5
Network Flow ◼ Can you give a good algorithm? ◼ Methodology 5: Approach to the optimum by a sequence of improvements. 5