
Size of graph The size of a graph: 01 0 0 …1 1 0 1 A= 0 1 0 11 Adjacency matrix:V2. 0 1 …4 1234 Adjacency list: V+2E for undirected graphs. 1:2 Each undirected edge is counted twice. 2:1,3,4 3:2,4 V+E for directed graphs. 4:2,3 ▣ Each directed edge is counted once. 6
Size of graph ◼ The size of a graph: ❑ Adjacency matrix: 𝑉 2 . ❑ Adjacency list: ◼ |𝑉| + 2|𝐸| for undirected graphs. ❑ Each undirected edge is counted twice. ◼ |𝑉| + |𝐸| for directed graphs. ❑ Each directed edge is counted once. 1: 2 2: 1, 3, 4 3: 2, 4 4: 2, 3 6
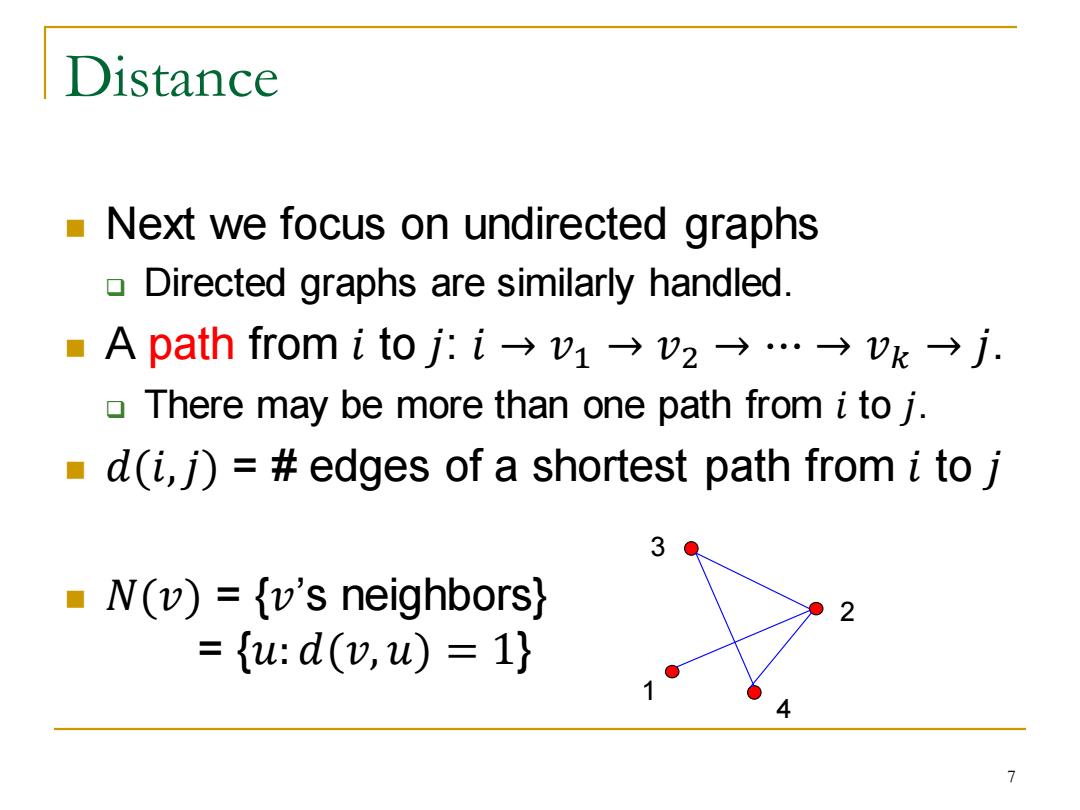
Distance Next we focus on undirected graphs Directed graphs are similarly handled. A path from i to j:i→v1→v2→…→vk→j: There may be more than one path from i to j. d(i,)=#edges of a shortest path from i to j 3 N(v)={v's neighbors) ={u:d(,u)=1}
Distance ◼ Next we focus on undirected graphs ❑ Directed graphs are similarly handled. ◼ A path from 𝑖 to 𝑗: 𝑖 → 𝑣1 → 𝑣2 → ⋯ → 𝑣𝑘 → 𝑗. ❑ There may be more than one path from 𝑖 to 𝑗. ◼ 𝑑(𝑖,𝑗) = # edges of a shortest path from 𝑖 to 𝑗 ◼ 𝑁(𝑣) = {𝑣’s neighbors} = {𝑢: 𝑑(𝑣, 𝑢) = 1} 3 1 2 4 7

A natural question:compute the distance and a shortest path between vertices os→t:st-distance s-all other vertices:Single-Source Shortest Paths 0 all vertices s all other vertices t:All-Pair Shortest paths 8
◼ A natural question: compute the distance and a shortest path between vertices ❑ 𝑠 → 𝑡: 𝑠𝑡-distance ❑ 𝑠 → all other vertices: Single-Source Shortest Paths ❑ all vertices 𝑠 → all other vertices 𝑡: All-Pair Shortest Paths 8
Why shortest paths? Google map for directions Optimal solution of Rubik's cube. Guess what's the number? Erd6s number
Why shortest paths? ◼ Google map for directions ◼ Optimal solution of Rubik’s cube. ❑ Guess what’s the number? ◼ Erdős number 9
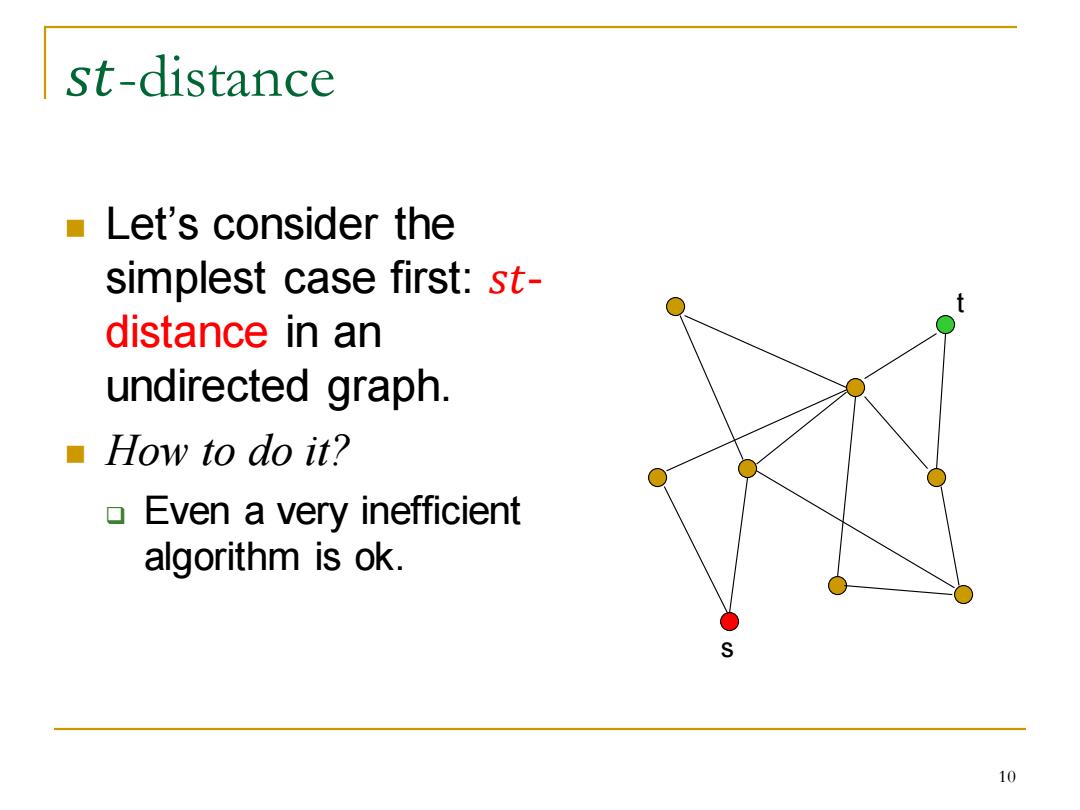
st-distance Let's consider the simplest case first:st- distance in an undirected graph. ■How to do it? Even a very inefficient algorithm is ok. S 10
𝑠𝑡-distance ◼ Let’s consider the simplest case first: 𝑠𝑡- distance in an undirected graph. ◼ How to do it? ❑ Even a very inefficient algorithm is ok. s t 10