
CSC3160: Design and Analysis of Algorithms Week 3: Greedy Algorithms Instructor: Shengyu Zhang 1
Instructor: Shengyu Zhang 1

Content Two problems Minimum Spanning Tree Huffman encoding One approach:greedy algorithms 2
Content ◼ Two problems ❑ Minimum Spanning Tree ❑ Huffman encoding ◼ One approach: greedy algorithms 2

Example 1:Minimum Spanning Tree 3
Example 1: Minimum Spanning Tree 3
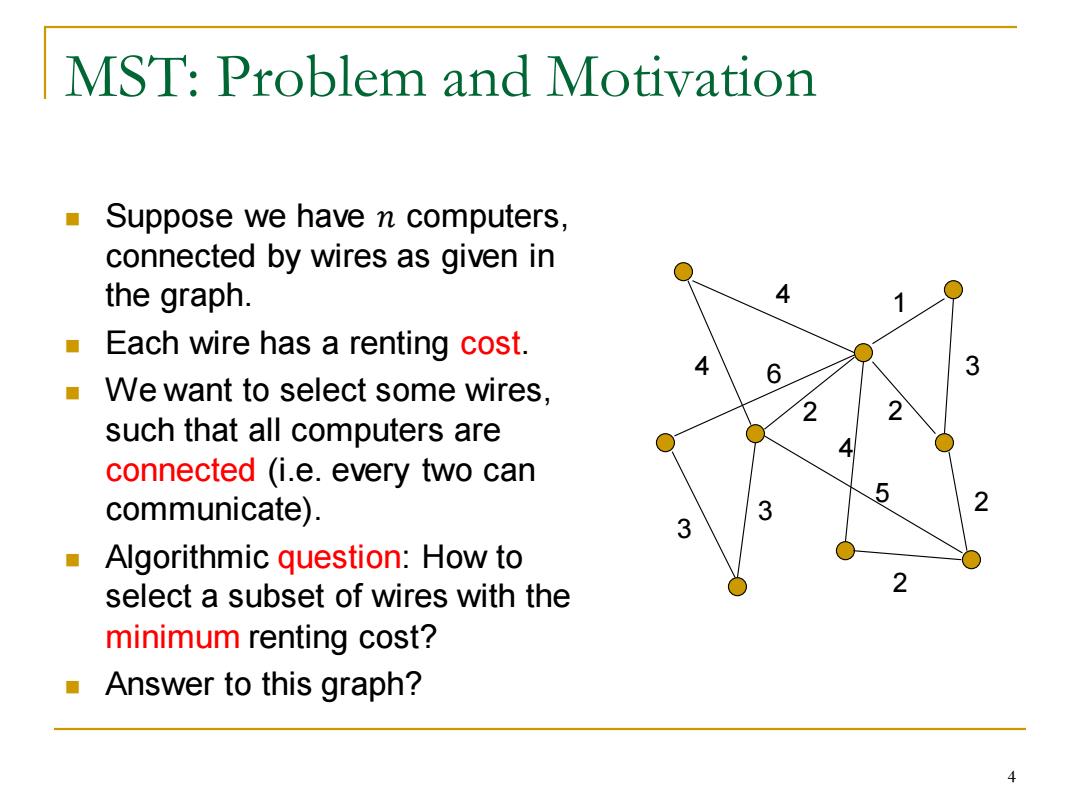
MST:Problem and Motivation Suppose we have n computers, connected by wires as given in the graph. 4 1 ■ Each wire has a renting cost. 4 6 3 ■ We want to select some wires, such that all computers are connected (i.e.every two can communicate). 3 Algorithmic question:How to select a subset of wires with the minimum renting cost? Answer to this graph?
MST: Problem and Motivation ◼ Suppose we have 𝑛 computers, connected by wires as given in the graph. ◼ Each wire has a renting cost. ◼ We want to select some wires, such that all computers are connected (i.e. every two can communicate). ◼ Algorithmic question: How to select a subset of wires with the minimum renting cost? ◼ Answer to this graph? 4 1 4 3 5 4 2 2 2 3 3 2 6 4
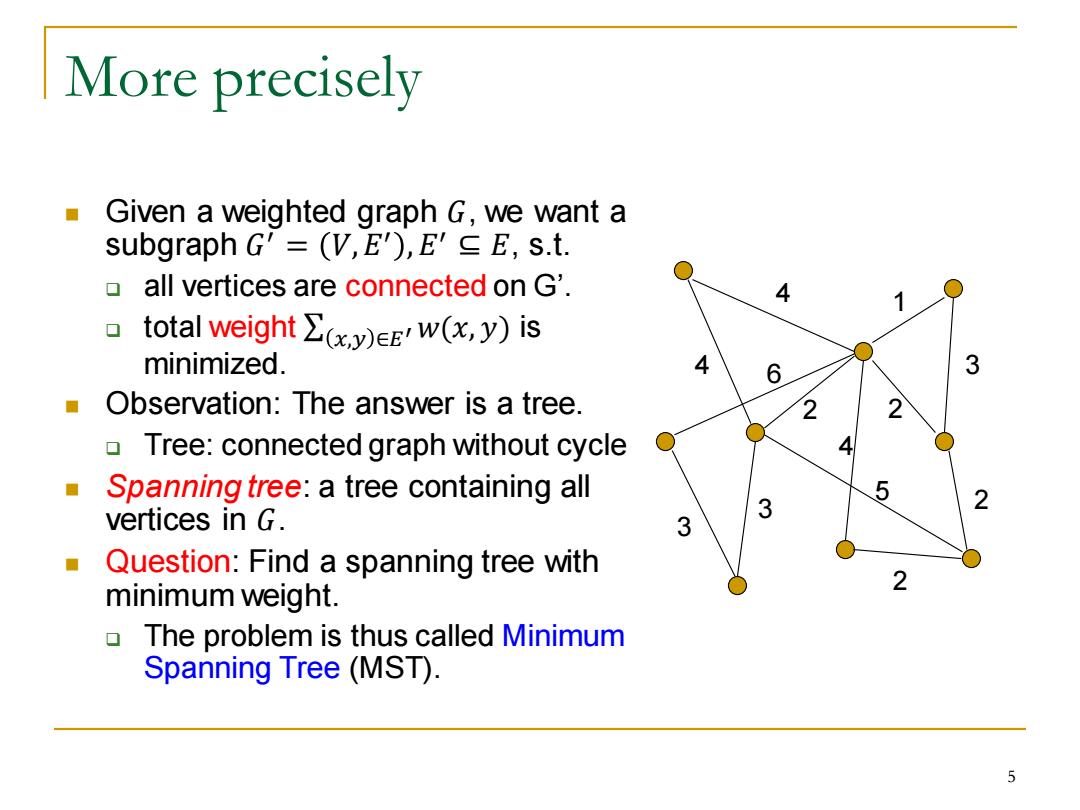
More precisely Given a weighted graph G,we want a subgraph G'=(V,E),E'C E,s.t. all vertices are connected on G'. 4 1 0 total weight (w(x,y)is minimized. 4 6 3 Observation:The answer is a tree. 2 Tree:connected graph without cycle Spanning tree:a tree containing all vertices in G. 3 3 Question:Find a spanning tree with 2 minimum weight. The problem is thus called Minimum Spanning Tree (MST). 5
More precisely ◼ Given a weighted graph 𝐺, we want a subgraph 𝐺 ′ = 𝑉,𝐸 ′ ,𝐸 ′ ⊆ 𝐸, s.t. ❑ all vertices are connected on G’. ❑ total weight σ 𝑥,𝑦 ∈𝐸′ 𝑤(𝑥, 𝑦) is minimized. ◼ Observation: The answer is a tree. ❑ Tree: connected graph without cycle ◼ Spanning tree: a tree containing all vertices in 𝐺. ◼ Question: Find a spanning tree with minimum weight. ❑ The problem is thus called Minimum Spanning Tree (MST). 4 1 4 3 5 4 2 2 2 3 3 2 6 5