
CSC3160: Design and Analysis of Algorithms Week 2: Single Source Shortest Paths Instructor: Shengyu Zhang
Instructor: Shengyu Zhang

Content Graphs:model,size,distance. Problem:shortest path Algorithms: BFS:unweighted Dijkstra:non-negative weights 0 Bellman-Ford:negative weights 2
Content ◼ Graphs: model, size, distance. ◼ Problem: shortest path. ◼ Algorithms: ❑ BFS: unweighted ❑ Dijkstra: non-negative weights ❑ Bellman-Ford: negative weights 2
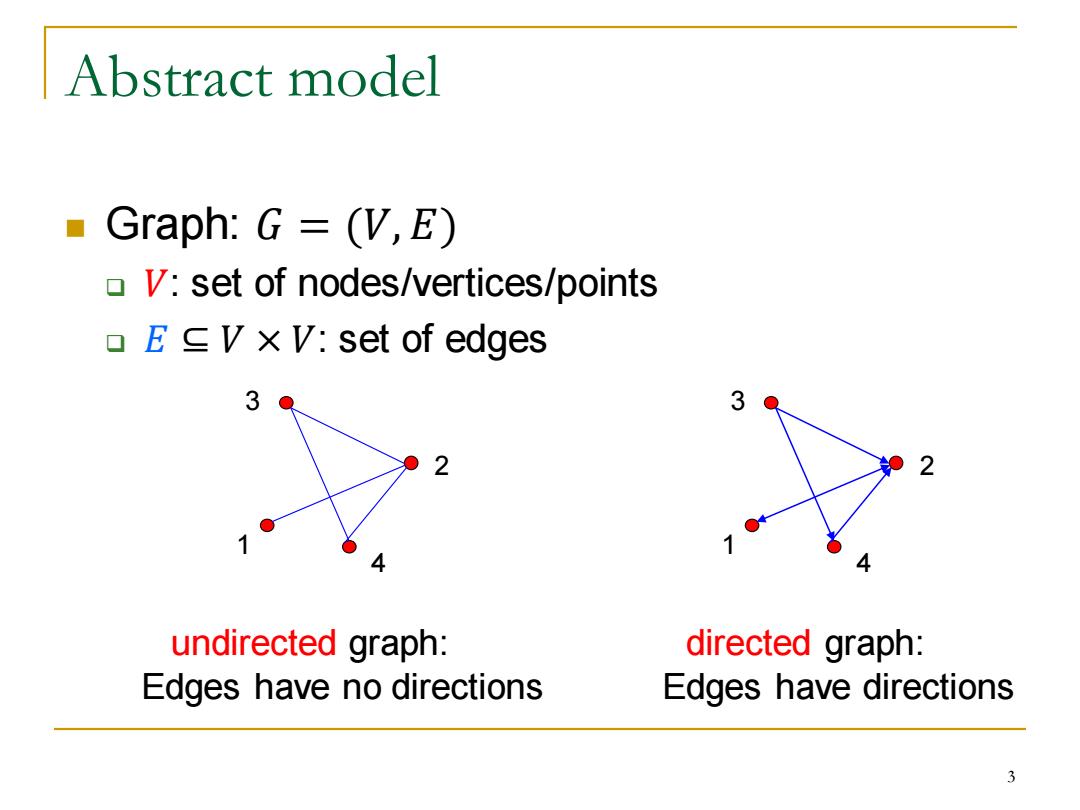
Abstract model ·Graph:G=(V,E) V:set of nodes/vertices/points EV xV:set of edges 3 3 undirected graph: directed graph: Edges have no directions Edges have directions 3
Abstract model ◼ Graph: 𝐺 = (𝑉, 𝐸) ❑ 𝑉: set of nodes/vertices/points ❑ 𝐸 ⊆ 𝑉 × 𝑉: set of edges 3 1 2 4 undirected graph: Edges have no directions directed graph: Edges have directions 3 1 2 4 3

Graph,graph,graph... Why graph?There are lots of graph examples in our lives. Name one. Information:W.citation Social:co-actor,dating,messenger,communities Technological:Internet,power grids,airline routes Biological:Neural networks,food web,blood vessels
Graph, graph, graph… ◼ Why graph? There are lots of graph examples in our lives. ◼ Name one. ❑ Information: WWW, citation ❑ Social: co-actor, dating, messenger, communities ❑ Technological: Internet, power grids, airline routes ❑ Biological: Neural networks, food web, blood vessels ❑ … 4
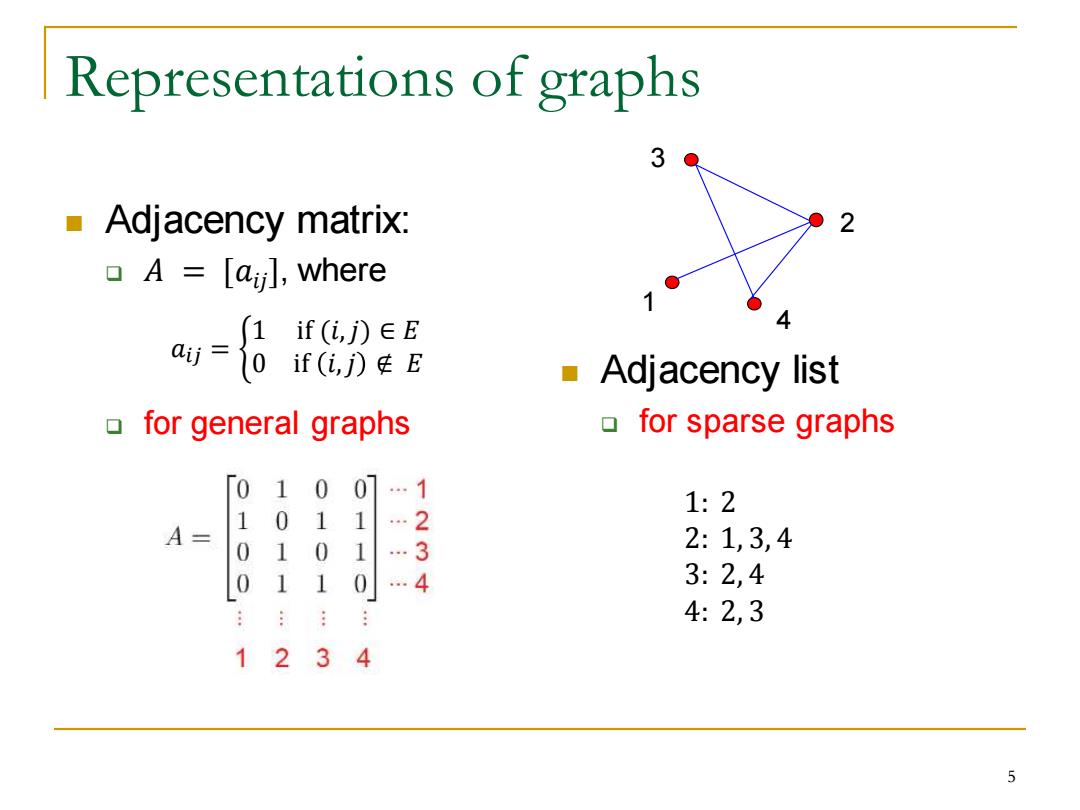
Representations of graphs Adjacency matrix: 2 ▣A=[al,where if (i,j)EE if(i,jE Adjacency list ofor general graphs o for sparse graphs 0 10 07 …1 1 1:2 1 01 A= …2 0 1 0 1 3 2:1,3,4 01 1 0 .…4 3:2,4 4:2,3 12 3 4 5
Representations of graphs ◼ Adjacency matrix: ❑ 𝐴 = [𝑎𝑖𝑗], where ❑ for general graphs ◼ Adjacency list ❑ for sparse graphs 3 1 2 4 𝑎𝑖𝑗 = ቊ 1 if (𝑖,𝑗) ∈ 𝐸 0 if 𝑖,𝑗 ∉ 𝐸 1: 2 2: 1, 3, 4 3: 2, 4 4: 2, 3 5