
RSA的快速模指数运算 。平方-乘的伪代码 输入:m,e=ek.12k-l+ek-22k-2+.+e12l+e0,n 输出:c=ne mod n c=1 for i=k-1 downto 0 利用“平方-乘”算法计算m3的具体过程 { i ei C c=c2 mod n 3 1 c=1×1modn,c=1 Xm mod n 2 1 c=m2 mod n,c=m2Xm mod n if ef=1 c=cm mod n 1 0 c=(m3)2 mod n } 0 1 c=(m6)2 mod n,c=m12Xm mod n return c
RSA的快速模指数运算 平方-乘的伪代码 输入:m, e=ek-12 k-1+ek-22 k-2+…+e12 1+e0,n 输出:c≡me mod n c=1 for i=k-1 downto 0 { c≡c 2 mod n if ei=1 c≡cm mod n } return c i ei c 3 1 c≡1×1 mod n, c≡1×m mod n 2 1 c≡m2 mod n, c≡m2×m mod n 1 0 c≡(m3 ) 2 mod n 0 1 c≡(m6 ) 2 mod n, c≡m12×m mod n 利用“平方-乘”算法计算m13的具体过程

RSA的安全性 ●RSA的安全性 ■基于分解大整数的困难性假定。如果RSA的模数被成功地分解 为pXq,则立即获得 mn)=(p-1)(q-1) ■从而能够确定e模om)的乘法逆元d,即 d后e1 mod o(n)
RSA的安全性 RSA的安全性 基于分解大整数的困难性假定。如果RSA的模数n被成功地分解 为p×q,则立即获得 (n)=(p-1)(q-1) 从而能够确定e模(n)的乘法逆元d,即 d≡e -1 mod (n)

RSA的安全性 。对RSA的攻击—数学攻击 ■用数学方法攻击RSA的途径有以下三种: ①分解n为两个素因子。这样就可以计算(m)=(p-1)(g-1),从而计 算出私钥el mod c(n)。 ②直接确定om)而不先确定p和q。这同样可以确定仨el mod o(n)。 ③直接确定d而不先确定p(n)。 ■对RSA的密码分析主要集中于第一种攻击方法
RSA的安全性 对RSA的攻击——数学攻击 用数学方法攻击RSA的途径有以下三种: ①分解n为两个素因子。这样就可以计算(n)=(p-1)(q-1),从而计 算出私钥d≡e -1 mod (n)。 ②直接确定(n)而不先确定p和q。这同样可以确定d≡e -1 mod (n)。 ③直接确定d而不先确定(n)。 对RSA的密码分析主要集中于第一种攻击方法
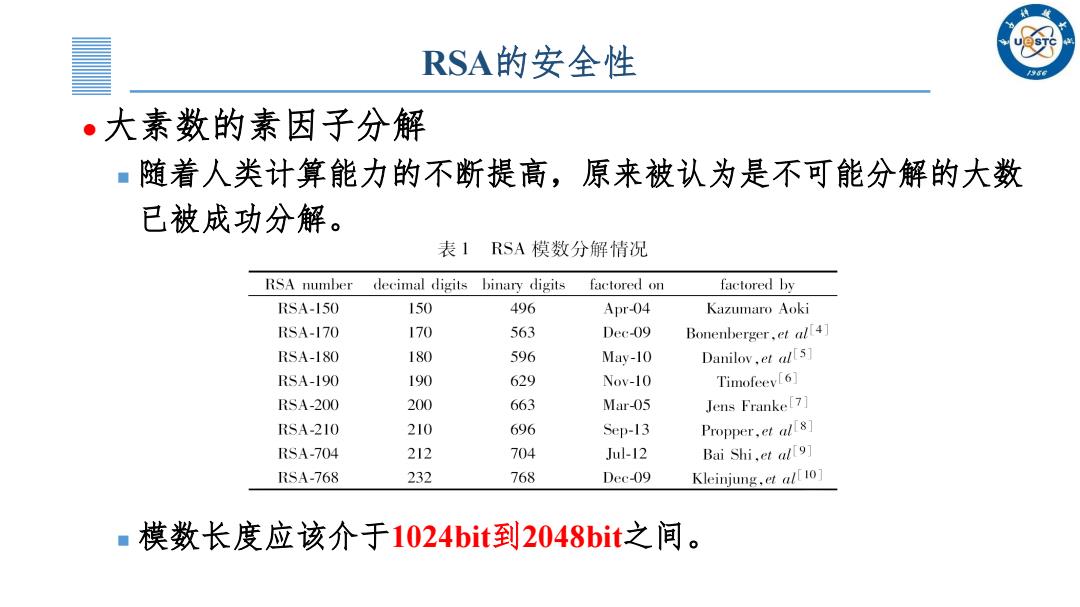
RSA的安全性 。大素数的素因子分解 ■随着人类计算能力的不断提高,原来被认为是不可能分解的大数 已被成功分解。 表1RSA模数分解情况 RSA number decimal digits binary digits factored on factored by RSA-150 150 496 Apr-04 Kazumaro Aoki RSA-170 170 563 Dec-09 Bonenberger,et al[4] RSA-180 180 596 May-10 Danilov,et al[5] RSA-190 190 629 Nov-10 Timofeev[6] RSA-200 200 663 Mar-05 Jens Franke[7] RSA-210 210 696 Sep-13 Propper,et al[8] RSA-704 212 704 Jul-12 Bai Shi,et al[9] RSA-768 232 768 Dec-09 Kleinjung,et alf 0] ■模数长度应该介于1024bit到2048bit之间
RSA的安全性 大素数的素因子分解 随着人类计算能力的不断提高,原来被认为是不可能分解的大数 已被成功分解。 模数长度应该介于1024bit到2048bit之间

RSA的安全性 ·对p和q的限制条件: ①p和q的长度应该相差仅几位。 ②-1)和(q-1)都应有一个大的素因子。 ③gcdp-1,q-1)应该较小。 ④若e<n且dkn4,则d很容易被确定
RSA的安全性 对p和q的限制条件: ①p和q的长度应该相差仅几位。 ②(p-1)和(q-1)都应有一个大的素因子。 ③gcd(p-1, q-1)应该较小。 ④若e<n且d<n 1/4,则d很容易被确定