
第11卷第3期 智能系统学报 Vol.11 No.3 2016年6月 CAAI Transactions on Intelligent Systems Jun.2016 D0I:10.11992/is.201603046 网络出版地址:http://www.cnki.net/kcms/detail/23.1538.TP.20160513.0957.034.html 一种基于少量标签的改进迁移模糊聚类 王跃,杨燕,王红军 (西南交通大学信息科学与技术学院,四川成都610031) 摘要:传统聚类算法难以利用已有的历史信息,尤其是数据被污染的情况下聚类结果不理想:半监督聚类常用于 数据中有部分标签的情况。在源数据有少量标签的情况下,提出半监督混合C均值聚类算法(SS-FPCM):基于迁移 学习框架,针对负迁移问题对算法进行修正,提出了防止负迁移的半监督迁移算法(TSS-FPCM):最后,为了充分借 鉴源数据的信息,利用“代表点”来代替源数据类信息,融入算法中再次迁移得到改善的半监督迁移算法(TSS FPCM)。实验表明,3个算法能够有效的利用源数据提高聚类性能。SS-FPCM与TSS-FPCM可以利用源数据的少量 标签数据,而TSS-FPCM算法结合了标签数据与“代表点”两个有效信息,在数据信息匮乏、数据被污染的情况下得 到较好的聚类结果。 关键词:聚类:迁移学习:半监督:可能性C均值:模糊C均值 中图分类号:TP301文献标志码:A文章编号:1673-4785(2016)03-0310-08 中文引用格式:王跃,杨燕,王红军.一种基于少量标签的改进迁移模糊聚类[J].智能系统学报,2016,11(3):310-317. 英文引用格式:VANG Yue,YANG Yan,WANG Hongjun.An improved transfer fuzzy clustering with few labels[J].CAAI trans- actions on intelligent systems,2016,11(3):310-317. An improved transfer fuzzy clustering with few labels WANG Yue,YANG Yan,WANG Hongjun (School of Information Science and Technology,Southwest Jiaotong University,Chengdu 610031,China) Abstract:In the traditional clustering algorithm,it is difficult to utilize existing historical information,which tends to be less effective in cases in which the data is contaminated.The semi-supervised clustering algorithm is often used in such circumstances,wherein the target data has some labeled examples.For situations in which the source data has partially labeled samples,in this paper,we propose a semi-supervised fuzzy possibilistic C-means algo- rithm (SS-FPCM).Based on the transfer learning framework,we use a transfer semi-supervised fuzzy possibilistic C-means algorithm (TSS-FPCM)to avoid the negative transfer learning problem.Finally,in order to make full use of source data information,we use representative points to replace the source data class.Thus,we have developed an improved transfer semi-supervised fuzzy possibilistic C-means algorithm (ITSS-FPCM).The experimental results demonstrate that these three algorithms may be used to improve the clustering performance by using source data ef- fectively,as compared with other clustering algorithms.Moreover,the SS-FPCM and TSS-FPCM algorithms exploit partially labeled data from the source,while the ITSS-FPCM algorithm combines the labeled data and "representa- tive points,"for cases having insufficient data information or contaminated data,and an excellent clustering result is attained. Keywords:clustering;transfer learning;semi-supervised;possibilistic C-means;fuzzy C-means 传统的聚类算法在拥有大量数据的情况下能够 污染的情况,传统的聚类算法存在着不足。 在不同的场景下发挥各自的作用,当数据匮乏、噪声 近年来,迁移学习的成果逐渐丰富,研究表明, 迁移学习能够有效地解决数据量不足、数据受污染 收稿日期:2016-03-19.网络出版日期:2016-05-13. 基金项目:国家自然科学基金项目(61170111,61572407,61134002): 和信息丢失等问题。文献[1]根据迁移学习中源领 四川省料技支撑计划项目(2014SZ0207). 通信作者:杨燕.E-mail:yang@swjtu.ed血.cn 域和目标领域中是否含有标签,可以将迁移学习划
第 11 卷第 3 期 智 能 系 统 学 报 Vol.11 №.3 2016 年 6 月 CAAI Transactions on Intelligent Systems Jun. 2016 DOI:10.11992 / tis.201603046 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.TP.20160513.0957.034.html 一种基于少量标签的改进迁移模糊聚类 王跃,杨燕,王红军 (西南交通大学 信息科学与技术学院,四川 成都 610031) 摘 要:传统聚类算法难以利用已有的历史信息,尤其是数据被污染的情况下聚类结果不理想;半监督聚类常用于 数据中有部分标签的情况。 在源数据有少量标签的情况下,提出半监督混合 C 均值聚类算法( SS⁃FPCM);基于迁移 学习框架,针对负迁移问题对算法进行修正,提出了防止负迁移的半监督迁移算法(TSS⁃FPCM);最后,为了充分借 鉴源数据的信息,利用“代表点” 来代替源数据类信息,融入算法中再次迁移得到改善的半监督迁移算法( ITSS⁃ FPCM)。 实验表明,3 个算法能够有效的利用源数据提高聚类性能。 SS⁃FPCM 与 TSS⁃FPCM 可以利用源数据的少量 标签数据,而 ITSS⁃FPCM 算法结合了标签数据与“代表点”两个有效信息,在数据信息匮乏、数据被污染的情况下得 到较好的聚类结果。 关键词:聚类;迁移学习;半监督;可能性 C 均值;模糊 C 均值 中图分类号:TP301 文献标志码:A 文章编号:1673⁃4785(2016)03⁃0310⁃08 中文引用格式:王跃,杨燕,王红军.一种基于少量标签的改进迁移模糊聚类[J]. 智能系统学报, 2016, 11(3): 310⁃317. 英文引用格式:WANG Yue, YANG Yan, WANG Hongjun.An improved transfer fuzzy clustering with few labels[J]. CAAI trans⁃ actions on intelligent systems, 2016,11(3): 310⁃317. An improved transfer fuzzy clustering with few labels WANG Yue, YANG Yan, WANG Hongjun (School of Information Science and Technology, Southwest Jiaotong University, Chengdu 610031, China) Abstract:In the traditional clustering algorithm, it is difficult to utilize existing historical information, which tends to be less effective in cases in which the data is contaminated. The semi⁃supervised clustering algorithm is often used in such circumstances, wherein the target data has some labeled examples. For situations in which the source data has partially labeled samples, in this paper, we propose a semi⁃supervised fuzzy possibilistic C⁃means algo⁃ rithm (SS⁃FPCM). Based on the transfer learning framework, we use a transfer semi⁃supervised fuzzy possibilistic C⁃means algorithm (TSS⁃FPCM) to avoid the negative transfer learning problem. Finally, in order to make full use of source data information, we use representative points to replace the source data class. Thus, we have developed an improved transfer semi⁃supervised fuzzy possibilistic C⁃means algorithm (ITSS⁃FPCM). The experimental results demonstrate that these three algorithms may be used to improve the clustering performance by using source data ef⁃ fectively, as compared with other clustering algorithms. Moreover, the SS⁃FPCM and TSS⁃FPCM algorithms exploit partially labeled data from the source, while the ITSS⁃FPCM algorithm combines the labeled data and " representa⁃ tive points," for cases having insufficient data information or contaminated data, and an excellent clustering result is attained. Keywords:clustering; transfer learning; semi⁃supervised; possibilistic C⁃means; fuzzy C⁃means 收稿日期:2016⁃03⁃19. 网络出版日期:2016⁃05⁃13. 基金项目:国家自然科学基金项目( 61170111, 61572407, 61134002); 四川省科技支撑计划项目(2014SZ0207). 通信作者:杨燕. E⁃mail: yyang@ swjtu.edu.cn. 传统的聚类算法在拥有大量数据的情况下能够 在不同的场景下发挥各自的作用,当数据匮乏、噪声 污染的情况,传统的聚类算法存在着不足。 近年来,迁移学习的成果逐渐丰富,研究表明, 迁移学习能够有效地解决数据量不足、数据受污染 和信息丢失等问题。 文献[1]根据迁移学习中源领 域和目标领域中是否含有标签,可以将迁移学习划

第3期 王跃,等:一种基于少量标签的改进迁移模糊聚类 ·311- 分为3类:归纳迁移学习、直推式迁移学习和无监督 N 迁移学习。现有的迁移学习在分类领域已有较多研 k=1 究成果20),而在聚类领域迁移学习理论和方法相 —,i (5) 对则要少很多。文献[11-12]在聚类领域利用了迁 移学习的理论。 1.2PFCM聚类算法 半监督聚类是半监督学习与聚类分析相结合的 FPCM是建立在FCM和PCM基础上的算法, 研究领域,文献[13]提出了不同情况下的半监督聚 它将两者结合在一起,FPCM的目标函数定义为 类算法,并取得了不错的效果。 J= 文献[14]将经典的模糊C均值算法1s(FCM) 正d形 (6) 与可能性C均值[6](PCM)算法进行改进,提出了 式中:m>1,m>1,0≤,≤1,约束条件为 模糊可能性聚类算法(FPCM)。本文探讨在源领域 2a=1,i (7) 有少量标签的情况下,如何指导目标域进行聚类,提 出半监督模糊可能性C均值聚类算法(SS-FPCM), 2=1,k (8) 并针对负迁移问题对算法进行改进,提出了防止负 通过最小化目标函数,可以得到以下迭代优化 迁移的半监督迁移算法(TSS-FPCM),同时,用代表 公式: 点代替源领域的数据进行数据迁移,得到改善的半 监督迁移算法(TSS-FPCM),并进行了实验验证。 [周 (9) 1相关算法介绍 Vi,k (10) 1.1PCM聚类算法 PCM聚类算法放松了传统FCM聚类算法中对 于隶属度矩阵的约束,隶属度不再是对1的共享。 ∑(u候+) .Vi 对于给定数据集X={xIk=1,2,…,N},x4∈R,包 N (11) 含N个样本,分成C个类别,T= (+) {t4li=1,2,…,C;k=1,2,…,N}是可能划分矩阵,t 1.3半监督聚类算法 表示第k个样本x:属于第i类的可能性,聚类中心 对于一些有着一部分标签的数据集,在文献 为V={yIi=1,2,…,C},其中y:表示第i个聚类中 [17]中,Pedrycz提出了基于部分标签的模糊聚类 心。PCM目标函数定义为 算法(SS-F℃M),算法的核心思想是利用现有的分类 信息,并把它作为优化程序的一部分。 为了区分标记数据与未标记数据,引入向量矩 式中:t4∈[0,1],0<∑a≤N,m为模糊指数, 阵B={bIk=1,2,…,N},如果x是已知标签样本 b=1,否则bs=0。并且记类别属性F= 和7:的取值分别为式(2)和式(3),K的取值一般取 {fli=1,2,…,C;k=1,2,…,N},如果x4属于第i K=1。 类,那么f4=1:否则f=0。在引人B和F后,Pe d=‖x4-v:2=(x4-v:)T(x4-v)(2) dycz将模糊参数m取值为2,其目标函数为 ∑md n:sK (ua -fab)'da N—,K>0 (3) 含a (12) 最小化目标函数可以得到可能性矩阵和聚类中 2半监督迁移模糊聚类算法 心的迭代式(4)和式(5): 2.1半监督模糊可能性C均值聚类算法 1 .Vi,k 4 对半监督FCM算法进行研究可以发现,上文中 的B和F的功能相似,保留下F并对FPCM的目标 函数做如下改进:
分为 3 类:归纳迁移学习、直推式迁移学习和无监督 迁移学习。 现有的迁移学习在分类领域已有较多研 究成果[2⁃10] ,而在聚类领域迁移学习理论和方法相 对则要少很多。 文献[11⁃12]在聚类领域利用了迁 移学习的理论。 半监督聚类是半监督学习与聚类分析相结合的 研究领域,文献[13]提出了不同情况下的半监督聚 类算法,并取得了不错的效果。 文献[14]将经典的模糊 C 均值算法[15] (FCM) 与可能性 C 均值[16] ( PCM) 算法进行改进,提出了 模糊可能性聚类算法(FPCM)。 本文探讨在源领域 有少量标签的情况下,如何指导目标域进行聚类,提 出半监督模糊可能性 C 均值聚类算法( SS⁃FPCM), 并针对负迁移问题对算法进行改进,提出了防止负 迁移的半监督迁移算法(TSS⁃FPCM),同时,用代表 点代替源领域的数据进行数据迁移,得到改善的半 监督迁移算法(ITSS⁃FPCM),并进行了实验验证。 1 相关算法介绍 1.1 PCM 聚类算法 PCM 聚类算法放松了传统 FCM 聚类算法中对 于隶属度矩阵的约束,隶属度不再是对 1 的共享。 对于给定数据集 X = xk { | k = 1,2,…,N} ,xk∈R d ,包 含 N 个 样 本, 分 成 C 个 类 别, T = t ik { | i = 1,2,…,C;k = 1,2,…,N}是可能划分矩阵,t ik 表示第 k 个样本 xk 属于第 i 类的可能性,聚类中心 为 V = vi { | i = 1,2,…,C} ,其中 vi 表示第 i 个聚类中 心。 PCM 目标函数定义为 J = ∑ C i = 1 ∑ N k = 1 t m ikd 2 ik + ∑ C i = 1 ηi∑ N k = 1 1 - t ik ( ) m d 2 ik (1) 式中: t ik ∈ [0,1] ,0 < ∑ N k = 1 t m ik ≤N,m为模糊指数,d 2 ik 和 ηi 的取值分别为式(2) 和式(3),K 的取值一般取 K = 1。 d 2 ik = ‖xk - vi‖2 = xk - vi ( ) T xk - vi ( ) (2) ηi = K ∑ N k = 1 t m ikd 2 ik ∑ N k = 1 t m ik ,K > 0 (3) 最小化目标函数可以得到可能性矩阵和聚类中 心的迭代式(4)和式(5): t ik = 1 1 + d 2 ik ηi æ è ç ö ø ÷ 1 m-1 ,∀i,k (4) vi = ∑ N k = 1 t m ik xk ∑ N k = 1 t m ik ,∀i (5) 1.2 PFCM 聚类算法 FPCM 是建立在 FCM 和 PCM 基础上的算法, 它将两者结合在一起 ,FPCM 的目标函数定义为 J = ∑ C i = 1 ∑ N k = 1 u m ik + t η ik ( ) d 2 ik (6) 式中:m>1,η>1,0≤ik,t ik≤1,约束条件为 ∑ N k = 1 t ik = 1,∀i (7) ∑ C i = 1 uik = 1,∀k (8) 通过最小化目标函数,可以得到以下迭代优化 公式: uik = ∑ C j = 1 d 2 ik d 2 ij æ è ç ö ø ÷ 1 m-1 é ë ê ê ù û ú ú -1 ,∀i,k (9) t ik = ∑ N j = 1 d 2 ik d 2 ij æ è ç ö ø ÷ 1 η-1 é ë ê ê ù û ú ú -1 ,∀i,k (10) vi = ∑ N k = 1 u m ik + t η ik ( ) xk ∑ N k = 1 u m ik + t η ik ( ) ,∀i (11) 1.3 半监督聚类算法 对于一些有着一部分标签的数据集,在文献 [17]中,Pedrycz 提出了基于部分标签的模糊聚类 算法(SS⁃FCM),算法的核心思想是利用现有的分类 信息,并把它作为优化程序的一部分。 为了区分标记数据与未标记数据,引入向量矩 阵 B = bk { | k = 1,2,…,N} ,如果 xk 是已知标签样本 bk = 1, 否 则 bk = 0。 并 且 记 类 别 属 性 F = f ik { | i = 1,2,…,C;k = 1,2,…,N} ,如果 xk 属于第 i 类,那么 f ik = 1;否则 f ik = 0。 在引入 B 和 F 后,Pe⁃ drycz 将模糊参数 m 取值为 2,其目标函数为 J = ∑ C i = 1 ∑ N k = 1 u 2 ikd 2 ik + α∑ C i = 1 ∑ N k = 1 uik - f ik bk ( ) 2 d 2 ik (12) 2 半监督迁移模糊聚类算法 2.1 半监督模糊可能性 C 均值聚类算法 对半监督 FCM 算法进行研究可以发现,上文中 的 B 和 F 的功能相似,保留下 F 并对 FPCM 的目标 函数做如下改进: 第 3 期 王跃,等:一种基于少量标签的改进迁移模糊聚类 ·311·

.312 智能系统学报 第11卷 N J= ∑∑(a+B)d+u (ua -fa)'di J= a+)+ (13) u4-f)] s.t.a≥0,B≥0,w>0,0≤ut,tk≤1 最小化目标函数,可以得到迭代表达式: s.t. a≥0,B≥0,ω>0,0≤4法,tt≤1 N+M Vi,k (14) -IVk.IVi (17) 不直接使用式(13)的目标函数而改用式(17)》 a+(1-∑f) 的目标函数,当参数ω趋于0的时候,前者相当于 证= +ωfk,i,k 将M个源数据当作未知标签加入到目标领域中进 a+w 行无监督混合C均值聚类,而后者则等于认为这些 数据没有用处而舍弃。可以发现前者无法控制加入 (15) 源数据后所可能造成的负迁移现象影响聚类结果, ∑【a匠+B+wua-f)]x 而后者则可以有效避免该情况。 ,Hi 最小化目标函数可以得到: N a暖+假+ua-fa)门 d d -1 k≤N (16) 通过不断迭代优化隶属度矩阵最终获得我们需 ωd,告d + N<k≤N+M 要的划分。改进的半监督模糊可能性C均值算法 (SS-FPCM)能够通过a、B控制FPCM中FCM和 (18) -1 PCM的权重,通过参数ω的变化控制已知标签在算 k≤N 法中所占的比重。 2.2历史标签数据的迁移 1 迁移学习可以将历史场景(也叫源数据)中获 1+a 1 一+ f,N<k≤N+M 取需要的数据或者信息,用于指导当前场景(又成 1+a 为目标数据),当历史场景的信息与当前场景的相 关性足够大时,可以从中得到潜藏的信息。在当历 (19) 史场景没有任何指导信的数据(无任何标签信息) V+V 时,文献[11-12]针对这种情况分别做出了自己的 (时tB)tu】 (oaiBit (u-fa)) N+I -,i 研究。 N+M 当源数据有少量的标签时候,可以很直观地想 三(@Hu2a哈时ur)y k=N+1 到,将这些数据提取出来,加入到当前场景,一起进 (20) 行聚类,以期待能够指导当前场景。前面提到了半 2.3改进的半监督迁移算法 监督FPCM聚类算法能够有效利用标签进行聚类, 在历史场景中,除了少量的标签信息,还有大量 便可以直接引用式(13)的目标函数。但是,在迁移 的未标记数据,这些数据量远远大于已标记数据,同 学习中负迁移是难以避免的一个问题,如果历史场 样可以从中获取需要的信息来帮助当前场景。直接 景与当前场景相关性并不大。那么历史数据的标签 将大量未标记数据加入当前场景中进行聚类大大增 很可能对当前场景产生不良影响,造成负迁移现象。 加了计算量。 针对这个问题,对式(13)进行改造,提出避免负迁 在历史场景中,为了减少计算量,可以使用一个 移的半监督迁移聚类算法(TS-FPCM)。 “代表点”来表示一个类,而不仅仅是文献[11]中的 假设历史场景中有M个已知标签样本,将数据 聚类中心:这个点既可以是聚类中心,也可以是数据 提取放在目标数据的后面,构成新的目标数据集 中的真实样本点,将庞大的数据变为有限的几个点。 X'={xk=1,2,…,N,N+1,…,N+M},x∈R,其 为了能够有效地利用“代表点”,给定代表点集 中后M个数据为历史场景中的已知样本,根据数据 合Xr={xIi=1,2,…,C},C表示聚类个数,重新定 集提出新的目标函数为 义新的距离函数为
J = ∑ C i = 1 ∑ N k = 1 αu 2 ik + βt 2 ik ( ) d 2 ik + ω∑ C i = 1 ∑ N k = 1 uik - f ik ( ) 2 d 2 ik (13) s.t. α ≥ 0, β ≥ 0, ω > 0, 0 ≤ uik, t ik ≤ 1 最小化目标函数,可以得到迭代表达式: t ik = ∑ N j = 1 d 2 ik d 2 ij æ è ç ö ø ÷ é ë ê ê ù û ú ú -1 ,∀i,k (14) uik = 1 α + ω α + ω 1 - ∑ C j = 1 f ( jk ) ∑ C j = 1 d 2 ik d 2 jk + ωf ik,∀i,k (15) vi = ∑ N k = 1 αu 2 ik + βt 2 ik + ω uik - f ik ( ) 2 [ ] xk ∑ N k = 1 αu 2 ik + βt 2 ik + ω uik - f ik ( ) 2 [ ] ,∀i (16) 通过不断迭代优化隶属度矩阵最终获得我们需 要的划分。 改进的半监督模糊可能性 C 均值算法 (SS⁃FPCM) 能够通过 α、 β 控制 FPCM 中 FCM 和 PCM 的权重,通过参数 ω 的变化控制已知标签在算 法中所占的比重。 2.2 历史标签数据的迁移 迁移学习可以将历史场景(也叫源数据) 中获 取需要的数据或者信息,用于指导当前场景(又成 为目标数据),当历史场景的信息与当前场景的相 关性足够大时,可以从中得到潜藏的信息。 在当历 史场景没有任何指导信的数据(无任何标签信息) 时,文献[11⁃12] 针对这种情况分别做出了自己的 研究。 当源数据有少量的标签时候,可以很直观地想 到,将这些数据提取出来,加入到当前场景,一起进 行聚类,以期待能够指导当前场景。 前面提到了半 监督 FPCM 聚类算法能够有效利用标签进行聚类, 便可以直接引用式(13)的目标函数。 但是,在迁移 学习中负迁移是难以避免的一个问题,如果历史场 景与当前场景相关性并不大。 那么历史数据的标签 很可能对当前场景产生不良影响,造成负迁移现象。 针对这个问题,对式(13)进行改造,提出避免负迁 移的半监督迁移聚类算法(TSS⁃FPCM)。 假设历史场景中有 M 个已知标签样本,将数据 提取放在目标数据的后面,构成新的目标数据集 X′= xk { k = 1,2,…,N,N+1,…,N+M} , xk ∈ R d , 其 中后 M 个数据为历史场景中的已知样本,根据数据 集提出新的目标函数为 J = ∑ C i = 1 ∑ N k = 1 αu 2 ik + βt 2 ik ( ) d 2 ik + ω ∑ C i = 1 ∑ N+M k = N+1 αu 2 ik + βt 2 ik ( ) d 2 ik + ∑ C i = 1 ∑ N+M k = N+1 uik - f ik ( ) 2 d 2 [ ik ] s.t. α ≥ 0, β ≥ 0, ω > 0, 0 ≤ uik, t ik ≤ 1 ∑ C i = 1 uik = 1∀k, ∑ N+M k = 1 t ik = 1∀i (17) 不直接使用式(13)的目标函数而改用式(17) 的目标函数,当参数 ω 趋于 0 的时候,前者相当于 将 M 个源数据当作未知标签加入到目标领域中进 行无监督混合 C 均值聚类,而后者则等于认为这些 数据没有用处而舍弃。 可以发现前者无法控制加入 源数据后所可能造成的负迁移现象影响聚类结果, 而后者则可以有效避免该情况。 最小化目标函数可以得到: t ik = ∑ N j = 1 d 2 ik d 2 ij + ∑ N+M j = N+1 d 2 ik ωd 2 ij æ è ç ö ø ÷ -1 , k ≤ N ∑ N j = 1 ωd 2 ik d 2 ij + ∑ N+M j = N+1 d 2 ik d 2 ij æ è ç ö ø ÷ -1 , N < k ≤ N + M ì î í ï ï ï ï ïï (18) uik = ∑ C j = 1 d 2 ik d 2 jk æ è ç ö ø ÷ -1 , k ≤ N 1 - 1 1 + α∑ C j = 1 f jk ∑ C j = 1 d 2 ik d 2 jk + 1 1 + α f ik, N < k ≤ N + M ì î í ï ï ï ï ï ï ï ï (19) vi = ∑ N k =1 αu 2 ik + βt 2 ik ( ) xk + ω∑ N+M k =N+1 αu 2 ik + βt 2 ik + uik - f ik ( ) 2 { } xk ∑ N k =1 αu 2 ik + βt 2 ik ( )+ ω∑ N+M k =N+1 αu 2 ik + βt 2 ik + uik - f ik ( ) 2 { } xk ,∀i (20) 2.3 改进的半监督迁移算法 在历史场景中,除了少量的标签信息,还有大量 的未标记数据,这些数据量远远大于已标记数据,同 样可以从中获取需要的信息来帮助当前场景。 直接 将大量未标记数据加入当前场景中进行聚类大大增 加了计算量。 在历史场景中,为了减少计算量,可以使用一个 “代表点”来表示一个类,而不仅仅是文献[11]中的 聚类中心;这个点既可以是聚类中心,也可以是数据 中的真实样本点,将庞大的数据变为有限的几个点。 为了能够有效地利用“代表点”,给定代表点集 合 XX^ = { ^xi | i = 1,2,…,C},C 表示聚类个数,重新定 义新的距离函数为 ·312· 智 能 系 统 学 报 第 11 卷

第3期 王跃,等:一种基于少量标签的改进迁移模糊聚类 ·313. =川x-%2+y1x-x2+Yy-x2 V+1 为了获得其迭 (21) 式中y:和y2为权重因子,用于调节历史中心的重 代表达式,利用拉格朗日极值优化表达式,首先构造 要程度,将代表点作为有效信息迁移到当前场景中 Lagrange表达式: 来。新的目标函数如式(22): Q=宫a+时)+ (au2+Ba)正+ 叫套三am+金2三0 i=1k=W+1 (22) 克芝,-密 三A-含)+2-宫)(2四) i=1k=N+1 式中入k与0:为Lagrange乘子。 式中:a≥0,B≥0,ω>0,0≤u,tk≤1, 令aQ/aV=0,解得: 列)+阳+m)叉1o N+M N+M 三+ k=N+l N+l I+W[E(am4+B的)+u三(a+B民+:-fW] =N-t (24) 令aQ/a入.=0,可以得到: 使用同样得方法,可以求得t的迭代表达式: 含=1 (25) V+U k≤N 令aQ/au4=0,对于0<k≤N可以解得: 2 (26) N+M d N<k≤N+M 将式(26)代入式(25),解得: (31) (27) 2.4改进的半监督迁移算法描述 根据上一节的公式,TSS-FPCM的表述如下: 再将入代回式(26),得到: 算法1ITSS-FPCM算法 输入前N个数据样本为目标数据,后M个为 (28) 已知标签的历史数据的数据样本X'= 同理,对于N<k≤N+M,可以求出: {xIk=1,2,…,N,N+1,…,N+M},聚类个数C,最 1 大迭代次数L,当前迭代次数(=1,源数据类代表点 1一1+a ,相关参数aB、w、Y1和Y2,阈值E。 (29) 输出聚类中心":,隶属度矩阵u和概率矩 阵t法o 1)初始化聚类中心”:,根据已知标签构造矩阵 合并式(28)和(29)可以得到最终表达式: F,初始化目标函数=0。 2)根据表达式(30)更新v。 k≤N 3)根据表达式(31)更新", 4)根据表达式(24)更新":。 1 5)l=l+1,计算新的目标函数0,如果J0- wk=1-1+a 1+Qt, N<k≤N+M -<6,或者>L跳到第6),否则,跳到2)。 6)聚类中心,隶属度矩阵v和概率矩阵v法。 3 实验结果 (30) 为了验证算法的有效性,实验使用了人工数据
d ?2 ik = ‖xk - vi‖2 + γ1 ‖xk - x ^ i‖2 + γ2 ‖vi - x ^ i‖2 (21) 式中 γ1 和 γ2 为权重因子,用于调节历史中心的重 要程度,将代表点作为有效信息迁移到当前场景中 来。 新的目标函数如式(22): J = ∑ C i = 1 ∑ N k = 1 αu 2 ik + βt 2 ik ( ) d ? 2 ik + ω ∑ C i = 1 ∑ N+M k = N+1 αu 2 ik + βt 2 ik ( ) d ? 2 { ik + ∑ C i = 1 ∑ N+M k = N+1 uik - f ik ( ) 2 d ? 2 ik ] (22) 式中: α ≥ 0, β ≥ 0, ω > 0, 0 ≤ uik, t ik ≤ 1, ∑ C i = 1 uik = 1,∀k, ∑ N+M k = 1 t ik = 1,∀i。 为了获得其迭 代表达式,利用拉格朗日极值优化表达式,首先构造 Lagrange 表达式: Q = ∑ C i = 1 ∑ N k = 1 αu 2 ik + βt 2 ik ( ) d ? 2 ik + ω ∑ C i = 1 ∑ N+M k =N+1 αu 2 ik + βt 2 ik ( ) d ? 2 [ ik +∑ C i = 1 ∑ N+M k =N+1 uik - f ik ( ) 2 d ? 2 ik ] + ∑ N+M k = 1 λk 1 - ∑ C i = 1 ( uik ) + ∑ C i = 1 θi 1 - ∑ N+M k = 1 t ( ik ) (23) 式中 λk 与 θi 为 Lagrange 乘子。 令∂Q/ ∂Vi = 0,解得: vi = ∑ N k =1 αu 2 ik + βt 2 ik ( ) xk + γ2∑ N k =1 αu 2 ik + βt 2 ik ( ) x^ i + ω ∑ N+M k =N+1 αu 2 ik + βt 2 ik + uik - f ik ( ) 2 ( ) xk + γ2∑ N+M k =N+1 αu 2 ik + βt 2 ik + uik - f ik ( ) 2 ( ) x^ [ i] 1 + γ2 ( ) ∑ N k =1 αu 2 ik + βt 2 ik ( ) + ω∑ N+M k =N+1 αu 2 ik + βt 2 ik + uik - f ik ( ) 2 [ ( ) ] (24) 令∂Q/ ∂λk = 0,可以得到: ∑ C i = 1 uik = 1 (25) 令∂Q/ ∂uik = 0,对于 0<k≤N 可以解得: uik = λ 2αd ? 2 ik (26) 将式(26)代入式(25),解得: λ 2α = ∑ C i = 1 1 d ? 2 ik æ è çç ö ø ÷÷ -1 (27) 再将 λ 代回式(26),得到: uik = ∑ C j = 1 d ? 2 ik d ? 2 jk æ è ç ç ö ø ÷ ÷ -1 (28) 同理,对于 N<k≤N+M,可以求出: uik = 1 - 1 1 + α∑ C j = 1 f jk ∑ C j = 1 d ? 2 ik d ? 2 jk + 1 1 + α f ik (29) 合并式(28)和(29)可以得到最终表达式: uik = ∑ C j = 1 d ? 2 ik d ? 2 jk æ è ç ç ö ø ÷ ÷ -1 , k ≤ N 1 - 1 1 + α∑ C j = 1 f jk ∑ C j = 1 d ? 2 ik d ? 2 jk + 1 1 + α f ik, N < k ≤ N + M ì î í ï ï ï ï ï ï ï ï ïï (30) 使用同样得方法,可以求得 t ik的迭代表达式: t ik = ∑ N j = 1 d ? 2 ik d ? 2 ij + ∑ N+M j = N+1 d ? 2 ik ωd ? 2 ij æ è ç ç ö ø ÷ ÷ -1 , k ≤ N ∑ N j = 1 ωd ? 2 ik d ? 2 ij + ∑ N+M j = N+1 d ? 2 ik d ? 2 ij æ è ç ç ö ø ÷ ÷ -1 , N < k ≤ N + M ì î í ï ï ï ï ï ï (31) 2.4 改进的半监督迁移算法描述 根据上一节的公式,ITSS⁃FPCM 的表述如下: 算法 1 ITSS⁃FPCM 算法 输入 前 N 个数据样本为目标数据,后 M 个为 已 知 标 签 的 历 史 数 据 的 数 据 样 本 X′ = xk { | k = 1,2,…,N,N+1,…,N+M} ,聚类个数 C, 最 大迭代次数 L,当前迭代次数 l = 1,源数据类代表点 X^ ,相关参数 α、β、ω、γ1 和 γ2 ,阈值 ε。 输出 聚类中心 vi,隶属度矩阵 uik 和概率矩 阵 t ik。 1)初始化聚类中心 vi,根据已知标签构造矩阵 F,初始化目标函数 J (l)= 0。 2)根据表达式(30)更新 vik。 3)根据表达式(31)更新 vik。 4)根据表达式(24)更新 vi。 5)l = l + 1,计算新的目标函数 J (l) ,如果 J (l) - J (l-1) <ε,或者 l>L 跳到第 6),否则,跳到 2)。 6)聚类中心 vi,隶属度矩阵 vik和概率矩阵 vik。 3 实验结果 为了验证算法的有效性,实验使用了人工数据 第 3 期 王跃,等:一种基于少量标签的改进迁移模糊聚类 ·313·
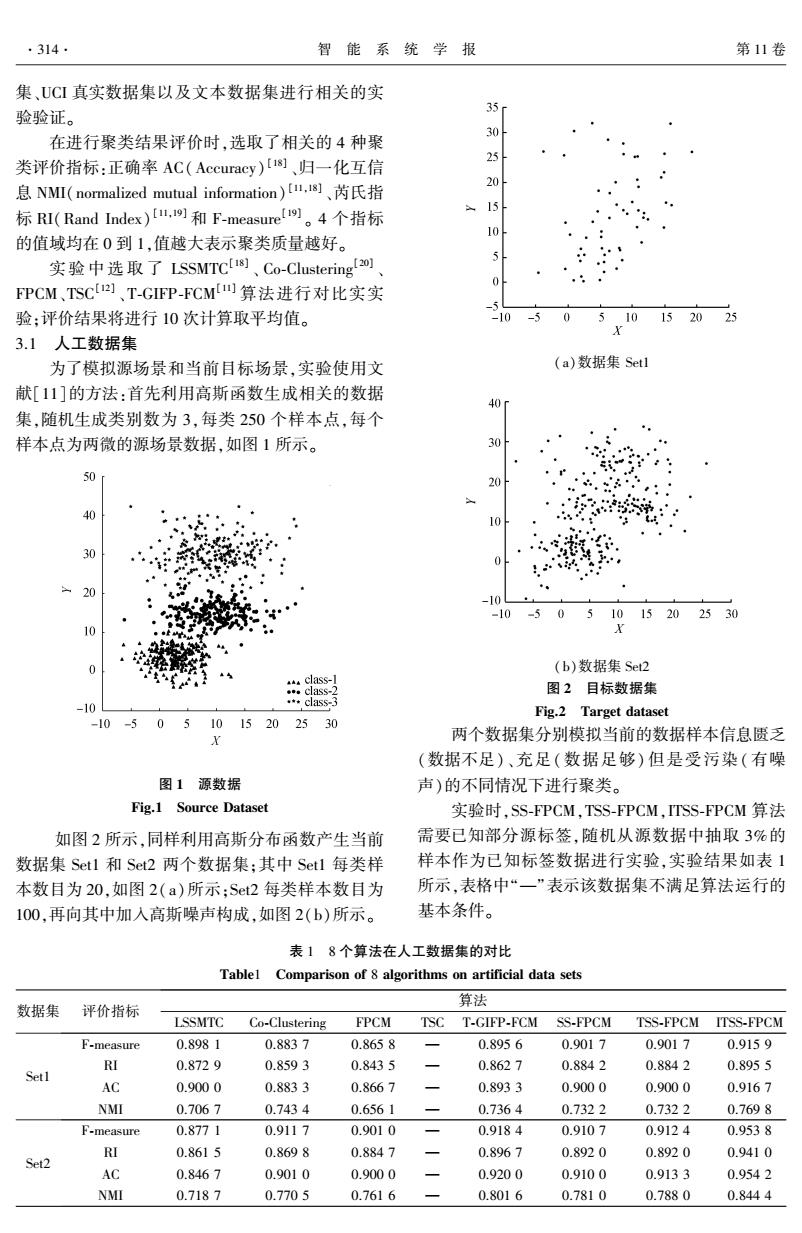
·314· 智能系统学报 第11卷 集、UCI真实数据集以及文本数据集进行相关的实 验验证。 35 在进行聚类结果评价时,选取了相关的4种聚 吃 类评价指标:正确率AC(Accuracy)u)、归一化互信 5 息NM(normalized mutual information),]、芮氏指 标RI(Rand Index),9和F-measure。4个指标 10 的值域均在0到1,值越大表示聚类质量越好。 实验中选取了LSSMTCU、Co-Clustering) 5 FPCM、TSC)]、T-GIP-FCM四算法进行对比实实 验:评价结果将进行10次计算取平均值。 -10 510 152025 3.1人工数据集 为了模拟源场景和当前目标场景,实验使用文 (a)数据集Setl 献[11]的方法:首先利用高斯函数生成相关的数据 40 集,随机生成类别数为3,每类250个样本点,每个 样本点为两微的源场景数据,如图1所示。 30 50 20 40 ·器 10 30 0 -10 -10 -5051015202530 0 24 0 (b)数据集Set2 class-1 .class-2 图2目标数据集 -10 *class-3 Fig.2 Target dataset -10-505 1015202530 k 两个数据集分别模拟当前的数据样本信息匮乏 (数据不足)、充足(数据足够)但是受污染(有噪 图1源数据 声)的不同情况下进行聚类。 Fig.1 Source Dataset 实验时,SS-FPCM,TSS-FPCM,ITSS-FPCM算法 如图2所示,同样利用高斯分布函数产生当前 需要已知部分源标签,随机从源数据中抽取3%的 数据集Set1和Set2两个数据集:其中Setl每类样 样本作为已知标签数据进行实验,实验结果如表1 本数目为20,如图2(a)所示:Set2每类样本数目为 所示,表格中“一”表示该数据集不满足算法运行的 100,再向其中加入高斯噪声构成,如图2(b)所示。 基本条件。 表18个算法在人工数据集的对比 Tablel Comparison of 8 algorithms on artificial data sets 算法 数据集 评价指标 LSSMTC Co-Clustering FPCM TSC T-GIFP-FCM SS-FPCM TSS-FPCM ITSS-FPCM F-measure 0.8981 0.8837 0.8658 0.8956 0.9017 0.9017 0.9159 RI 0.8729 0.8593 0.8435 0.8627 0.8842 0.8842 0.8955 Setl AC 0.9000 0.8833 0.8667 一 0.8933 0.9000 0.9000 0.9167 NMI 0.7067 0.7434 0.6561 一 0.7364 0.7322 0.7322 0.7698 F-measure 0.8771 0.9117 0.9010 一 0.9184 0.9107 0.9124 0.9538 RI 0.8615 0.8698 0.8847 0.8967 0.8920 0.8920 0.9410 Set2 AC 0.8467 0.9010 0.9000 0.9200 0.9100 0.9133 0.9542 NMI 0.7187 0.7705 0.7616 0.8016 0.7810 0.7880 0.8444
集、UCI 真实数据集以及文本数据集进行相关的实 验验证。 在进行聚类结果评价时,选取了相关的 4 种聚 类评价指标:正确率 AC(Accuracy) [18] 、归一化互信 息 NMI(normalized mutual information) [11,18] 、芮氏指 标 RI(Rand Index) [11,19] 和 F⁃measure [19] 。 4 个指标 的值域均在 0 到 1,值越大表示聚类质量越好。 实验 中 选 取 了 LSSMTC [18] 、 Co⁃Clustering [20] 、 FPCM、TSC [12] 、T⁃GIFP⁃FCM [11] 算法进行对比实实 验;评价结果将进行 10 次计算取平均值。 3.1 人工数据集 为了模拟源场景和当前目标场景,实验使用文 献[11]的方法:首先利用高斯函数生成相关的数据 集,随机生成类别数为 3,每类 250 个样本点,每个 样本点为两微的源场景数据,如图 1 所示。 图 1 源数据 Fig.1 Source Dataset 如图 2 所示,同样利用高斯分布函数产生当前 数据集 Set1 和 Set2 两个数据集;其中 Set1 每类样 本数目为 20,如图 2(a)所示;Set2 每类样本数目为 100,再向其中加入高斯噪声构成,如图 2(b)所示。 (a)数据集 Set1 (b)数据集 Set2 图 2 目标数据集 Fig.2 Target dataset 两个数据集分别模拟当前的数据样本信息匮乏 (数据不足)、充足(数据足够) 但是受污染(有噪 声)的不同情况下进行聚类。 实验时,SS⁃FPCM,TSS⁃FPCM,ITSS⁃FPCM 算法 需要已知部分源标签,随机从源数据中抽取 3%的 样本作为已知标签数据进行实验,实验结果如表 1 所示,表格中“—”表示该数据集不满足算法运行的 基本条件。 表 1 8 个算法在人工数据集的对比 Table1 Comparison of 8 algorithms on artificial data sets 数据集 评价指标 算法 LSSMTC Co⁃Clustering FPCM TSC T⁃GIFP⁃FCM SS⁃FPCM TSS⁃FPCM ITSS⁃FPCM Set1 F⁃measure 0.898 1 0.883 7 0.865 8 — 0.895 6 0.901 7 0.901 7 0.915 9 RI 0.872 9 0.859 3 0.843 5 — 0.862 7 0.884 2 0.884 2 0.895 5 AC 0.900 0 0.883 3 0.866 7 — 0.893 3 0.900 0 0.900 0 0.916 7 NMI 0.706 7 0.743 4 0.656 1 — 0.736 4 0.732 2 0.732 2 0.769 8 Set2 F⁃measure 0.877 1 0.911 7 0.901 0 — 0.918 4 0.910 7 0.912 4 0.953 8 RI 0.861 5 0.869 8 0.884 7 — 0.896 7 0.892 0 0.892 0 0.941 0 AC 0.846 7 0.901 0 0.900 0 — 0.920 0 0.910 0 0.913 3 0.954 2 NMI 0.718 7 0.770 5 0.761 6 — 0.801 6 0.781 0 0.788 0 0.844 4 ·314· 智 能 系 统 学 报 第 11 卷