
第11卷第3期 智能系统学报 Vol.11 No.3 2016年6月 CAAI Transactions on Intelligent Systems Jun.2016 D0I:10.11992/is.201603038 网络出版地址:http://www.enki..net/kcms/detail/23.1538.TP.20160513.0925.028.html 基于置换检验的聚类结果评估 谷飞洋,田博,张思萌,陈征,何增有 (大连理工大学软件学院,辽宁大连116621) 摘要:对聚类结果,传统的评估方法不能从统计意义上对结果评估。ECP是一种新颖的基于置换检验的评估算 法。ECP直接对聚类结果进行置换检验从而计算出p-value。为了测试ECP的效果,利用了UCI中的iris,wine, yest数据集对算法进行评测。实验结果表明,ECP可以在能够接受的时间内运算出比较准确的实验结果。 关键词:聚类:聚类评估;统计检验:置换检验 中图分类号:TP393文献标志码:A文章编号:1673-4785(2016)03-0301-09 中文引用格式:谷飞洋,田博,张思萌,等.基于置换检验的聚类结果评估[J].智能系统学报,2016,11(3):301-309. 英文引用格式:GU Feiyang,.TIAN Bo,.ZHANG Simeng,etal.Statistical evaluation of the clustering results based on permutation test[J].CAAI transactions on intelligent systems,2016,11(3):301-309. Statistical evaluation of the clustering results based on permutation test GU Feiyang,TIAN Bo,ZHANG Simeng,CHEN Zheng,HE Zengyou (Software School,Dalian University of Technology,Dalian 116621,China) Abstract:For the result of clustering,tranditional methods of evalution couldn't assess the result in statistics.We propose a new algorithm called ECP(Statistical evaluation of Clustering based on Permutation test)which uses per- mutation test to evaluate the result of clustering.To evaluate the performance of the algorithm,we use the data sets, iris,wine,yeast,from UCI datasets.Experimental results show that the performance of the algorithm is good. Keywords:clustering;clustering evaluation;statistical test;permutation test 随着获得的数据越来越多,利用机器学习、数据 houette-ndex,Dunn-ndex等。这些函数能够评估 挖掘[1]等手段从数据中获取潜在的知识变得越来 聚类结果,但是这些函数评估出来的结果往往没有 越重要。然而如何评估挖掘出来的信息,即评估数 一个比较好的可以参考的值。即一个评估值计算出 据挖掘结果的质量是一个十分重要的问题。只有一 来之后得到的只是一个评估值,至于这个值达到什 个好的评估方法,才能保证挖掘算法发现高质量的 么标准能够接受并不能确定。利用统计方法评估聚 信息。聚类41是数据挖掘领域一个很重要的分 类结果的算法很少,其主要原因是聚类的特殊性与 支。同时,聚类的应用也越来越广泛。随着聚类的 复杂性使传统的统计方法很难用到聚类质量评估 广泛应用,如何有效地评估聚类结果的质量[6]成 上。近年来有一些利用随机方法来评估聚类结果的 为一个重要的研究课题。虽然评估聚类结果的重要 研究,但也存在一定的问题。本文根据存在的问题 性一点不亚于挖掘算法本身,但是评估方面却没有 提出了一种基于置换检验的评估方法。 受到它应有的重视。 针对聚类,现有的方法主要是用评价函数对聚 1相关研究 类结果评估。这种函数一般分3种类型:紧密型、分 1.1利用簇结构评估聚类质量 散型和连接型。常见的评估函数有DB-Index,Si- 该方法先对原始数据聚类,然后将原始数据集 按照一定的约束随机置换抽样构造新的数据集。抽 收稿日期:2016-03-19.网络出版日期:2016-05-13 基金项目:国家自然科学基金项目(61572094). 样之后用同样的聚类算法对样本数据集进行聚类。 通信作者:何增有.E-mail:zyhc@dlut.cdu.cm
第 11 卷第 3 期 智 能 系 统 学 报 Vol.11 №.3 2016 年 6 月 CAAI Transactions on Intelligent Systems Jun. 2016 DOI:10.11992 / tis.201603038 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.TP.20160513.0925.028.html 基于置换检验的聚类结果评估 谷飞洋,田博,张思萌,陈征,何增有 (大连理工大学 软件学院, 辽宁 大连 116621) 摘 要:对聚类结果,传统的评估方法不能从统计意义上对结果评估。 ECP 是一种新颖的基于置换检验的评估算 法。 ECP 直接对聚类结果进行置换检验从而计算出 p ⁃value。 为了测试 ECP 的效果,利用了 UCI 中的 iris, wine, yeast 数据集对算法进行评测。 实验结果表明,ECP 可以在能够接受的时间内运算出比较准确的实验结果。 关键词:聚类;聚类评估; 统计检验;置换检验 中图分类号:TP393 文献标志码:A 文章编号:1673⁃4785(2016)03⁃0301⁃09 中文引用格式:谷飞洋,田博,张思萌,等.基于置换检验的聚类结果评估[J]. 智能系统学报, 2016, 11(3): 301⁃309. 英文引用格式:GU Feiyang, TIAN Bo, ZHANG Simeng, et al. Statistical evaluation of the clustering results based on permutation test[J]. CAAI transactions on intelligent systems, 2016,11(3): 301⁃309. Statistical evaluation of the clustering results based on permutation test GU Feiyang, TIAN Bo, ZHANG Simeng, CHEN Zheng, HE Zengyou (Software School, Dalian University of Technology, Dalian 116621, China) Abstract:For the result of clustering, tranditional methods of evalution couldn't assess the result in statistics. We propose a new algorithm called ECP(Statistical evaluation of Clustering based on Permutation test) which uses per⁃ mutation test to evaluate the result of clustering. To evaluate the performance of the algorithm, we use the data sets, iris, wine, yeast, from UCI datasets. Experimental results show that the performance of the algorithm is good. Keywords:clustering; clustering evaluation; statistical test; permutation test 收稿日期:2016⁃03⁃19. 网络出版日期:2016⁃05⁃13. 基金项目:国家自然科学基金项目(61572094). 通信作者:何增有. E⁃mail:zyhe@ dlut.edu.cn. 随着获得的数据越来越多,利用机器学习、数据 挖掘[1⁃3]等手段从数据中获取潜在的知识变得越来 越重要。 然而如何评估挖掘出来的信息,即评估数 据挖掘结果的质量是一个十分重要的问题。 只有一 个好的评估方法,才能保证挖掘算法发现高质量的 信息。 聚类[4⁃5] 是数据挖掘领域一个很重要的分 支。 同时,聚类的应用也越来越广泛。 随着聚类的 广泛应用,如何有效地评估聚类结果的质量[6⁃7] 成 为一个重要的研究课题。 虽然评估聚类结果的重要 性一点不亚于挖掘算法本身,但是评估方面却没有 受到它应有的重视。 针对聚类,现有的方法主要是用评价函数对聚 类结果评估。 这种函数一般分 3 种类型:紧密型、分 散型和连接型。 常见的评估函数有 DB⁃Index, Si⁃ houette⁃Index, Dunn⁃Index 等。 这些函数能够评估 聚类结果,但是这些函数评估出来的结果往往没有 一个比较好的可以参考的值。 即一个评估值计算出 来之后得到的只是一个评估值,至于这个值达到什 么标准能够接受并不能确定。 利用统计方法评估聚 类结果的算法很少,其主要原因是聚类的特殊性与 复杂性使传统的统计方法很难用到聚类质量评估 上。 近年来有一些利用随机方法来评估聚类结果的 研究,但也存在一定的问题。 本文根据存在的问题 提出了一种基于置换检验的评估方法。 1 相关研究 1.1 利用簇结构评估聚类质量 该方法先对原始数据聚类,然后将原始数据集 按照一定的约束随机置换抽样构造新的数据集。 抽 样之后用同样的聚类算法对样本数据集进行聚类

·302· 智能系统学报 第11卷 这样重复大量的次数后,再用评估函数(如DB-In- 量不同簇的两个最近成员的距离。全连接:度量不 dex)计算每个样本的函数值。如果原始数据集聚类 同簇的两个最远成员的距离。质心比较:度量不同 结果的函数值小于大部分随机构造的数据集聚类结 簇的中心点的距离。 果的函数值,那么说明挖掘出来的信息是可靠的,否 链接度链接度指簇中的元素成员至少要跟同 则说明聚类结果不可靠。更通俗一点,如果原来数 一个簇内的元素比较像。这个可以用来评估簇模型 据集没有好的簇结构,那么无论怎么聚类,结果都是 不是圆形或者球形的聚类结果,比如DBSCAN的聚 不好的。代表性的方法有最大熵模型抽样[】、矩阵 类结果。 元素交换9]等。利用数据集簇结构来评估聚类质 本文用一种无监督评估聚类质量的方法,Da- 量[]的方法能很好地评估出簇结构不好的聚类结 vies-Bouldin Index,DB_Index. 果。实验证实对不同数据集进行聚类,有明显簇结 构数据集的p-value会比没有明显簇结构的p-value DBI =1 、+s) max(D, =1 小很多。但是这种方法并不能准确评估聚类的质 式中:S表示第i个簇内的元素与质心的标准方差, 量。从某种意义上讲,这种方法更适合评估一个数 D,表示第i个簇与第j个簇质心间的欧几里德距 据集是否有好的簇结构。 离,k表示簇的数目。 1.2 SigClust DBI的思想是一个高质量的聚类结果需要满 SigClust!)认为如果一个数据集符合高斯分 足:同一个簇的各元素间相似度大,不同类之间的相 布,那么对这个数据集的任何分割都是不合理的。 似度小。在DBI中,分子越小意味着簇内元素相似 因此这个方法的前提假设是:一个单一的簇的元素 度越大,分母越大意味着簇间相似度越小。 符合高斯分布。SigClust主要是针对k=2的聚类评 2.2聚类评估的p-value 估。对于>2的情况,还没有比较好的解决办法。 给一个数据集X,用DB-ndex计算聚类结果的 l.3层次聚类的p-value计算 函数值为xox。数据集X所有可能的聚类结果的函 这种方法主要针对层次聚类的评估2,)。层 数值为x1,x,xN。置换检验的p-value定义为 次聚类后会形成一个二叉树。对二叉树上的每个节 点都进行置换检验,算出每个节点划分对应的p ∑a1(xn≤xo) value。这种算法的空假设为:当前节点的左子树和 N 右子树应该属于一个簇。如果算出p-value足够小 式中I是一个逻辑函数。当x.≤xo的情况下为1, 就说明空假设是一个小概率事件,应该拒绝。该方 否则为0。由于要枚举出所有的聚类方案的复杂度 法是将当前节点的左子树和右子树打乱,按照一定 是指数级别的,所以需要采取其他的策略。抽样出 的约束随机分配左子树和右子树的元素。抽样若干 所有情况的一个子集Y,并计算子集Y中所有元素 次后形成的随机样本集按照某种指标与原始划分对 的函数值为x1,x2,xw,其中N≤N。这时候置 比计算出p-value.。这个评估只能针对层次聚类,不 换检验的p-value被定义为 能对其他的聚类算法进行评估。另外这样计算出的 ∑N1(xn≤o) p-value只是每个节点上的p-value,并不是全局聚 N 类的p-value. 一些研究为了避免p-value为0的情况,将p-value 2基本概念 的定义修改为 2.1无监督聚类质量评估函数 1+1x≤w) 如果数据集中的元素没有类标签,聚类结果的 Ppeml N+1 评价就只能依赖数据集自身的特征和量值。在这种 这种方法把分子加1的理由是把x。也看作置 情况下,聚类的度量追求有3个目标:紧密度、分离 换检验一个样本的函数值。这就避免了得到p-vl- 度和链接度。 ue为0的试验结果。然而这种做法事实上是不太 紧密度簇中的每个元素应该彼此尽可能接 合理的。试想如果抽样999次没有发现比x。更小 近。紧密度的常用度量是方差,方差越小说明紧密 的统计值,这样草率地得出结论当前置换检验的结 度越大。 果为0.001显然太武断了。因为可能抽样99999次 分离度簇与簇之间应该充分分离。有3种常 依旧没有比x。更优的样本。那么依照这个计算公 用方法来度量两个不同簇之间的距离。单连接:度 式p-value又为0.000O1。而实际上p-value的值可
这样重复大量的次数后,再用评估函数(如 DB⁃In⁃ dex)计算每个样本的函数值。 如果原始数据集聚类 结果的函数值小于大部分随机构造的数据集聚类结 果的函数值,那么说明挖掘出来的信息是可靠的,否 则说明聚类结果不可靠。 更通俗一点,如果原来数 据集没有好的簇结构,那么无论怎么聚类,结果都是 不好的。 代表性的方法有最大熵模型抽样[8] 、矩阵 元素交换[9 ] 等。 利用数据集簇结构来评估聚类质 量[10]的方法能很好地评估出簇结构不好的聚类结 果。 实验证实对不同数据集进行聚类,有明显簇结 构数据集的 p⁃value 会比没有明显簇结构的 p⁃value 小很多。 但是这种方法并不能准确评估聚类的质 量。 从某种意义上讲,这种方法更适合评估一个数 据集是否有好的簇结构。 1.2 SigClust SigClust [11] 认为如果一个数据集符合高斯分 布,那么对这个数据集的任何分割都是不合理的。 因此这个方法的前提假设是:一个单一的簇的元素 符合高斯分布。 SigClust 主要是针对 k = 2 的聚类评 估。 对于 k>2 的情况,还没有比较好的解决办法。 1.3 层次聚类的 p ⁃value 计算 这种方法主要针对层次聚类的评估[12,13] 。 层 次聚类后会形成一个二叉树。 对二叉树上的每个节 点都进行置换检验,算出每个节点划分对应的 p ⁃ value。 这种算法的空假设为:当前节点的左子树和 右子树应该属于一个簇。 如果算出 p ⁃value 足够小 就说明空假设是一个小概率事件,应该拒绝。 该方 法是将当前节点的左子树和右子树打乱,按照一定 的约束随机分配左子树和右子树的元素。 抽样若干 次后形成的随机样本集按照某种指标与原始划分对 比计算出 p ⁃value。 这个评估只能针对层次聚类,不 能对其他的聚类算法进行评估。 另外这样计算出的 p ⁃value 只是每个节点上的 p ⁃value,并不是全局聚 类的 p ⁃value。 2 基本概念 2.1 无监督聚类质量评估函数 如果数据集中的元素没有类标签,聚类结果的 评价就只能依赖数据集自身的特征和量值。 在这种 情况下,聚类的度量追求有 3 个目标:紧密度、分离 度和链接度。 紧密度 簇中的每个元素应该彼此尽可能接 近。 紧密度的常用度量是方差,方差越小说明紧密 度越大。 分离度 簇与簇之间应该充分分离。 有 3 种常 用方法来度量两个不同簇之间的距离。 单连接:度 量不同簇的两个最近成员的距离。 全连接:度量不 同簇的两个最远成员的距离。 质心比较:度量不同 簇的中心点的距离。 链接度 链接度指簇中的元素成员至少要跟同 一个簇内的元素比较像。 这个可以用来评估簇模型 不是圆形或者球形的聚类结果,比如 DBSCAN 的聚 类结果。 本文用一种无监督评估聚类质量的方法, Da⁃ vies⁃Bouldin Index,即 DB_Index。 DBI = 1 k ∑ k i = 1 max( Si + Sj Dij ). 式中:Si表示第 i 个簇内的元素与质心的标准方差, Dij表示第 i 个簇与第 j 个簇质心间的欧几里德距 离,k 表示簇的数目。 DBI 的思想是一个高质量的聚类结果需要满 足:同一个簇的各元素间相似度大,不同类之间的相 似度小。 在 DBI 中,分子越小意味着簇内元素相似 度越大,分母越大意味着簇间相似度越小。 2.2 聚类评估的 p ⁃value 给一个数据集 X,用 DB⁃Index 计算聚类结果的 函数值为 x0 x0 。 数据集 X 所有可能的聚类结果的函 数值为 x1 ,x2 ,…xNall 。 置换检验的 p ⁃value 定义为 Pperm = ∑ Nall n = 1 I(xn ≤ x0 ) Nall 式中 I 是一个逻辑函数。 当 xn≤x0 的情况下为 1, 否则为 0。 由于要枚举出所有的聚类方案的复杂度 是指数级别的,所以需要采取其他的策略。 抽样出 所有情况的一个子集 Y,并计算子集 Y 中所有元素 的函数值为 x1 ,x2 ,…xN,其中 N≪ N all。 这时候置 换检验的 p ⁃value 被定义为 Pperm0 = ∑ N n = 1 I(xn ≤ x0 ) N . 一些研究为了避免 p ⁃value 为 0 的情况,将 p ⁃value 的定义修改为 Pperm1 = 1 + ∑ N n = 1 1(xn ≤ x0 ) N + 1 这种方法把分子加 1 的理由是把 x0 也看作置 换检验一个样本的函数值。 这就避免了得到 p ⁃val⁃ ue 为 0 的试验结果。 然而这种做法事实上是不太 合理的。 试想如果抽样 999 次没有发现比 x0 更小 的统计值,这样草率地得出结论当前置换检验的结 果为 0.001 显然太武断了。 因为可能抽样 99 999 次 依旧没有比 x0 更优的样本。 那么依照这个计算公 式 p ⁃value 又为0.000 01。 而实际上 p ⁃value 的值可 ·302· 智 能 系 统 学 报 第 11 卷

第3期 谷飞洋,等:基于置换检验的聚类结果评估 ·303· 能更小。因此本文把p-value的定义为PpemoP 法。算法1描述了抽样的过程。 置换检验的准确性取决于抽样的数目,一般的 算法1 Shuffle(CI,n) 置换检验抽样的次数都在1000次以上。为了得到 fori←-0ton-ldo 更精确的p-value抽样的次数越多越好,理想的情 index +rand()mod (i+1) 况是置换所有的可能。然而对于不同的数据集合, swap(CI,Cline CI,CI) 甚至很难预测需要执行多少次置换才能够得到比较 可以用数学归纳法进行证明算法1保证了每个 好的结果。往往为了得到更精确的值就会增大抽样 元素获得同一簇标号的概率是一样的。抽样的复杂 次数,但是增加抽样次数的代价是增加计算的复杂 度为O(n)。这样进行抽样N次,就得到了N个样 性。对于普通的数据集往往抽样次数达到10000 本。然后利用样本对原始聚类结果进行评估。用 次之后就不太容易提高抽样次数。而这样做又产生 DB-Index算出原始聚类的函数值x。与样本的函数 出了一个问题。如果一个聚类结果真实的p-value 值x1,x2,…,xw。有了这些值就能计算p-value了。 为0.000001。而抽样的次数只有10000次的话,那 具体算法如下。 么p-value为就为0了。针对这些问题,本文提出 算法2ECP1 了一种新的聚类评估方法,ECP,该方法能比较好地 用DB-Index计算聚类结果的函数值xo。 解决上文提到的问题。 fori←-1 to N do 3 基于置换检验的聚类结果评估 Shuffle(CI,n) 用DB-Index计算样本的函数值x 3.1基本思想 计算p-value 本文提出的置换检验方法将关注点锁定在了聚 一般情况下kn,因此DB-ndex的复杂度为 类的结果上。评估聚类结果的本质是看聚类算法对 数据集中元素的划分质量。从这个角度出发,可以 O(n×d)。抽样一次的复杂度是O(n),容易算出总 体复杂度为O(N×n×d)。这个复杂度还是比较高 枚举对数据集的划分,然后用评估函数算出枚举划 的。所以需要想一些方法来降低复杂度。N是抽样 分的函数值。如果绝大部分划分都没有要评估的聚 次数,期望越大越好。可以看到DB-ndex是影响复 类结果质量好的话,那么就说明要评估的聚类结果 杂度的主要因素。如果降低DB-ndex计算的复杂 质量比较好。相反地,就说明要评估的聚类结果质 性,那么就可以在相同的时间内抽取更多的样本来 量并不好。 因此对于一个聚类结果,本文定义了零假0: 提高p-value的准确度。本文发现了DB-ndex公式 当前聚类结果不是一个高质量的聚类。然后计算这 的特点,对上文提到的算法做了改进。 个零假设的p-value。如果这个p-value非常小,就认 3.2加速技巧 为这个划分结果可以接受,可以拒绝0。否则认为 首先选取聚类结果作为初始状态。然后随机交 这个聚类结果不能接受。 换一对簇标号不同的元素的簇标号。交换后把此时 定义数据集X是一个包含n个元素的d维数 的划分作为一个样本,直接计算DB-ndex的函数 值型矩阵。首先对数据集聚类,聚成k簇后每个元 值。接下来继续交换一对簇标号不同的元素的簇标 素都会归属于一个簇。我们对每个簇进行标号。标 号,交换后计算DB-Index的值。这样迭代N次后就 号从0开始,往后依次是1,2,…,k-1。定义C1为 会得到N个样本的函数值。利用这N个值就可以 第i个元素所属的簇标号。比如C13=2表示第3个 计算出p-value。整个算法流程如下。 元素属于标号为2的簇。 算法3ECP2 接下来是抽样。抽样要满足一定约束。本文定 用DB-Index计算聚类结果的函数值xo 义的约束是:样本中簇包含元素的数目要与待评估 for i1 to N do 聚类结果中簇中元素的数目保持一致。举个例子, 随机交换一对簇标号不同元素的簇标号 假设数据集元素数目n为100。划分成3簇,划分 用DB-Index计算抽样结果的函数值x, 簇中的数目分别是40、33、27。那么抽样出来的样 计算p-value 本也要满足这些条件,也就是要划分成3簇,并且簇 对比ECP1,ECP2只是修改了第3步的抽样方 中元素的数目也必须是40、33、27。具体的抽样方 法。为什么修改了抽样方法就可以增大抽样次数? 法:首先搜集所有元素的簇标号,然后将这些簇标 下面将仔细讨论DB-Index的计算过程。DB-ndex 号随机地分配给每个元素。其实这个过程是洗牌算 的计算公式为
能更小。 因此本文把 p ⁃value 的定义为 Pperm0Pecdf0 。 置换检验的准确性取决于抽样的数目,一般的 置换检验抽样的次数都在 1 000 次以上。 为了得到 更精确的 p ⁃value 抽样的次数越多越好,理想的情 况是置换所有的可能。 然而对于不同的数据集合, 甚至很难预测需要执行多少次置换才能够得到比较 好的结果。 往往为了得到更精确的值就会增大抽样 次数,但是增加抽样次数的代价是增加计算的复杂 性。 对于普通的数据集往往抽样次数达到 10 000 次之后就不太容易提高抽样次数。 而这样做又产生 出了一个问题。 如果一个聚类结果真实的 p ⁃value 为 0.000 001。 而抽样的次数只有 10 000 次的话,那 么 p ⁃value 为就为 0 了。 针对这些问题,本文提出 了一种新的聚类评估方法,ECP,该方法能比较好地 解决上文提到的问题。 3 基于置换检验的聚类结果评估 3.1 基本思想 本文提出的置换检验方法将关注点锁定在了聚 类的结果上。 评估聚类结果的本质是看聚类算法对 数据集中元素的划分质量。 从这个角度出发,可以 枚举对数据集的划分,然后用评估函数算出枚举划 分的函数值。 如果绝大部分划分都没有要评估的聚 类结果质量好的话,那么就说明要评估的聚类结果 质量比较好。 相反地,就说明要评估的聚类结果质 量并不好。 因此对于一个聚类结果,本文定义了零假 H0: 当前聚类结果不是一个高质量的聚类。 然后计算这 个零假设的 p⁃value。 如果这个 p⁃value 非常小,就认 为这个划分结果可以接受,可以拒绝 H0。 否则认为 这个聚类结果不能接受。 定义数据集 X 是一个包含 n 个元素的 d 维数 值型矩阵。 首先对数据集聚类,聚成 k 簇后每个元 素都会归属于一个簇。 我们对每个簇进行标号。 标 号从 0 开始,往后依次是 1,2, …,k-1。 定义CIi 为 第 i 个元素所属的簇标号。 比如CI3 = 2 表示第 3 个 元素属于标号为 2 的簇。 接下来是抽样。 抽样要满足一定约束。 本文定 义的约束是: 样本中簇包含元素的数目要与待评估 聚类结果中簇中元素的数目保持一致。 举个例子, 假设数据集元素数目 n 为 100。 划分成 3 簇,划分 簇中的数目分别是 40、33、27。 那么抽样出来的样 本也要满足这些条件,也就是要划分成 3 簇,并且簇 中元素的数目也必须是 40、33、27。 具体的抽样方 法: 首先搜集所有元素的簇标号,然后将这些簇标 号随机地分配给每个元素。 其实这个过程是洗牌算 法。 算法 1 描述了抽样的过程。 算法 1 Shuffle(CI, n) for i← 0 to n-1 do index ← rand() mod (i + 1) swap( CIi,CIindexCIi,CIindex ) 可以用数学归纳法进行证明算法 1 保证了每个 元素获得同一簇标号的概率是一样的。 抽样的复杂 度为 O(n)。 这样进行抽样 N 次,就得到了 N 个样 本。 然后利用样本对原始聚类结果进行评估。 用 DB⁃Index 算出原始聚类的函数值 x0 与样本的函数 值 x1 ,x2 ,…,xN。 有了这些值就能计算 p ⁃value 了。 具体算法如下。 算法 2 ECP1 用 DB⁃Index 计算聚类结果的函数值 x0 。 for i ← 1 to N do Shuffle(CI, n) 用 DB⁃Index 计算样本的函数值 xi 计算 p ⁃value 一般情况下 k≪n,因此 DB⁃Index 的复杂度为 O(n×d)。抽样一次的复杂度是 O( n),容易算出总 体复杂度为 O(N×n×d)。 这个复杂度还是比较高 的。 所以需要想一些方法来降低复杂度。 N 是抽样 次数,期望越大越好。 可以看到 DB⁃Index 是影响复 杂度的主要因素。 如果降低 DB⁃Index 计算的复杂 性,那么就可以在相同的时间内抽取更多的样本来 提高 p ⁃value 的准确度。 本文发现了 DB⁃Index 公式 的特点,对上文提到的算法做了改进。 3.2 加速技巧 首先选取聚类结果作为初始状态。 然后随机交 换一对簇标号不同的元素的簇标号。 交换后把此时 的划分作为一个样本,直接计算 DB⁃Index 的函数 值。 接下来继续交换一对簇标号不同的元素的簇标 号,交换后计算 DB⁃Index 的值。 这样迭代 N 次后就 会得到 N 个样本的函数值。 利用这 N 个值就可以 计算出 p ⁃value。 整个算法流程如下。 算法 3 ECP2 用 DB⁃Index 计算聚类结果的函数值 x0 for i← 1 to N do 随机交换一对簇标号不同元素的簇标号 用 DB⁃Index 计算抽样结果的函数值 xi 计算 p ⁃value 对比 ECP1,ECP2 只是修改了第 3 步的抽样方 法。 为什么修改了抽样方法就可以增大抽样次数? 下面将仔细讨论 DB⁃Index 的计算过程。 DB⁃Index 的计算公式为 第 3 期 谷飞洋,等:基于置换检验的聚类结果评估 ·303·

·304. 智能系统学报 第11卷 如果知道了样本DB-Index函数值的概率分布 DBI= max( Di 就可以根据原始聚类结果的函数值算出精确的p 由S,的定义可以得出: value了。聚类是一种半监督的机器学习,其本 质对元素所属类别的划分。如果对元素随机划分无 S:= 13- 穷次。那么质量特别高的划分的比例会很小。同样 m 的,质量极端差的划分占的比例也会很小。很大比 式中m,是簇zi中元素的数目。z,是簇i中第j个元 重的划分都介于它们之间。而正态分布的特点是: 素的属性向量,z是簇i质心的属性向量。由于数据 极端概率很小,中间的概率很大。经过对数据的分 是d维的,所以3-乏‖2就是各个维度的平方和。 析,聚类划分的DB-Index函数值比较符合正态分 因此可以单独对每一维计算,然后再把所有维度的 布。因此可以假设抽样样本DB-ndex的函数值符 平方相加即可: 合正态分布。实际上正态分布符合很多自然概率分 ∑3-2=∑∑(4-a,)2, 布的指标。下面要做的就是得到正态分布的参数。 对于一维的正态分布均值和方差用式(1)和(2) 式中:aa是簇i中第j个元素的第t个属性值,a,是 得到: 簇i质心的第t个属性值。下面直接讨论第t维的 计算方法: i=1 u= (1) ∑3-2∑∑(a-a)2 N m m d= (2) ∑(4-a2 N-1 有了概率分布函数,就能将原始聚类结果x。代 入概率分布算出p-value了。 其中: 这样估出概率分布函数实现了在整体复杂度没 有增加的前提下用较少的抽样得到更为精确p-val m m: ue的目的了。 因此 立.>) ∑3-2 2 m=1 2 本文利用公式P perm 一计算p-val- mi =1 mi N ∑,4,是筷中所有元素中第!维的平方和, u实际上是利用了大数定律。大数定律的本质是 如果有无穷次试验,事件出现的频率就会无限趋近 a,是簇i中所有元素第t维的平均值。所以为了计 于事件发生的概率。而由于抽样次数有限,本文假 算S,每一维只需要维护两个值就可以了:平方和与 设了DB-Index的函数值符合正态分布。不过对于 平均值。当簇标号交换的话,能在O(1)复杂度内 抽样N次后发现,已经有足够的样本可以精确算出 修正这两个值。修改完每个维度的这两个值后,就 p-vaue的话,就不需要用正态分布计算了。然而如 可以用DB-Index算出函数值了。 果抽样N次后没有足够的样本可以用大数定律精 可以看出修改一个簇的平方和与平均值复杂度 确地计算p-value的话就要拟合正态概率分布函数 是O(d)的。因此DB-Index的计算复杂度就是 了。对于有多少个样本满足x:≤x。算是足够呢? O(k×k×d)了。没有加速的DB-Index的计算复杂度 这是一个阈值问题。上边的过程总结起来如算 是O(n×d)。一般情况下,k≤n。所以这种方法的 法4。 效率有明显的提升。 算法4ECP 3.3更准确的p-vaue 抽样N次,算出每次的函数值x 上边提到计算DB-Index的方法的复杂度为 统计x:≤x。的数目M O(kx×d)。虽然相比于原先的计算方法已经优化 如果M≥Limit利用公式P,mo计算p-value 很多,但是对于p-value非常小的情况,可能依I旧由 否则,拟合正态概率分布算出p-value 于抽样数目有限而无法算出精确的p-value。这种 其中Limit是ECP的一个参数,是用Ppmo计算 情况下算出的p-value就会为O,然而这样的结果是 出p-value的最低数目限制。ECP不同于很多其他 不准确的。 的置换检验方法。这种方法实现了用较少的抽样计
DBI = 1 k ∑ k i = 1 max( Si + Sj Dij ). 由 Si 的定义可以得出: Si = ∑ mi j = 1‖zj - z‖2 mi . 式中 mi 是簇 zi 中元素的数目。 zj 是簇 i 中第 j 个元 素的属性向量,z 是簇 i 质心的属性向量。 由于数据 是 d 维的,所以‖zj -z‖2 就是各个维度的平方和。 因此可以单独对每一维计算,然后再把所有维度的 平方相加即可: ∑ mi j = 1‖zj - z‖2 = ∑ d t = 1∑ mi j = 1 (ajt - at) 2 , 式中:ajt是簇 i 中第 j 个元素的第 t 个属性值, at 是 簇 i 质心的第 t 个属性值。 下面直接讨论第 t 维的 计算方法: ∑ mi j = 1‖zj - z‖2 mi = ∑ d t = 1∑ mi j = 1 (ajt - at) 2 mi = ∑ d t = 1 ∑ mi j = 1 (ajt - at) 2 mi 其中: ∑ mi j = 1 (ajt - at) 2 mi = ∑ mi j = 1 ajt 2 mi - at 2 因此 ∑ mi j = 1‖zj - z‖2 mi = ∑ d t = 1 ∑ mi j = 1 ajt 2 mi - at 2 ∑ mi j = 1 ajt 2 是簇 i 中所有元素中第 t 维的平方和, at 是簇 i 中所有元素第 t 维的平均值。 所以为了计 算 Si,每一维只需要维护两个值就可以了:平方和与 平均值。 当簇标号交换的话,能在 O(1) 复杂度内 修正这两个值。 修改完每个维度的这两个值后,就 可以用 DB⁃Index 算出函数值了。 可以看出修改一个簇的平方和与平均值复杂度 是 O( d) 的。 因此 DB⁃Index 的计算复杂度就是 O(k×k×d)了。 没有加速的 DB⁃Index 的计算复杂度 是 O(n×d)。 一般情况下,k≪n。 所以这种方法的 效率有明显的提升。 3.3 更准确的 p ⁃value 上边提到计算 DB⁃Index 的方法的复杂度为 O(k×k×d)。 虽然相比于原先的计算方法已经优化 很多,但是对于 p ⁃value 非常小的情况,可能依旧由 于抽样数目有限而无法算出精确的 p ⁃value。 这种 情况下算出的 p ⁃value 就会为 0,然而这样的结果是 不准确的。 如果知道了样本 DB⁃Index 函数值的概率分布 就可以根据原始聚类结果的函数值算出精确的 p ⁃ value 了[14] 。 聚类是一种半监督的机器学习,其本 质对元素所属类别的划分。 如果对元素随机划分无 穷次。 那么质量特别高的划分的比例会很小。 同样 的,质量极端差的划分占的比例也会很小。 很大比 重的划分都介于它们之间。 而正态分布的特点是: 极端概率很小,中间的概率很大。 经过对数据的分 析,聚类划分的 DB⁃Index 函数值比较符合正态分 布。 因此可以假设抽样样本 DB⁃Index 的函数值符 合正态分布。 实际上正态分布符合很多自然概率分 布的指标。 下面要做的就是得到正态分布的参数。 对于一维的正态分布均值和方差用式(1) 和(2) 得到: μ = ∑ N i = 1 xi N (1) ∂ = (xi - x) 2 N - 1 (2) 有了概率分布函数,就能将原始聚类结果 x0 代 入概率分布算出 p ⁃value 了。 这样估出概率分布函数实现了在整体复杂度没 有增加的前提下用较少的抽样得到更为精确 p ⁃val⁃ ue 的目的了。 本文利用公式 Pperm0 ∑ N n = 1 I(yn > x0 ) N 计算 p ⁃val⁃ ue 实际上是利用了大数定律。 大数定律的本质是 如果有无穷次试验,事件出现的频率就会无限趋近 于事件发生的概率。 而由于抽样次数有限,本文假 设了 DB⁃Index 的函数值符合正态分布。 不过对于 抽样 N 次后发现,已经有足够的样本可以精确算出 p ⁃value 的话,就不需要用正态分布计算了。 然而如 果抽样 N 次后没有足够的样本可以用大数定律精 确地计算 p ⁃value 的话就要拟合正态概率分布函数 了。 对于有多少个样本满足 xi ≤ x0 算是足够呢? 这是一个阈值问题。 上边的过程总结起来如算 法 4。 算法 4 ECP 抽样 N 次,算出每次的函数值 xi 统计 xi≤x0 的数目 M 如果 M≥Limit 利用公式 Pperm0计算 p ⁃value 否则,拟合正态概率分布算出 p ⁃value 其中 Limit 是 ECP 的一个参数,是用 Pperm0 计算 出 p ⁃value 的最低数目限制。 ECP 不同于很多其他 的置换检验方法。 这种方法实现了用较少的抽样计 ·304· 智 能 系 统 学 报 第 11 卷
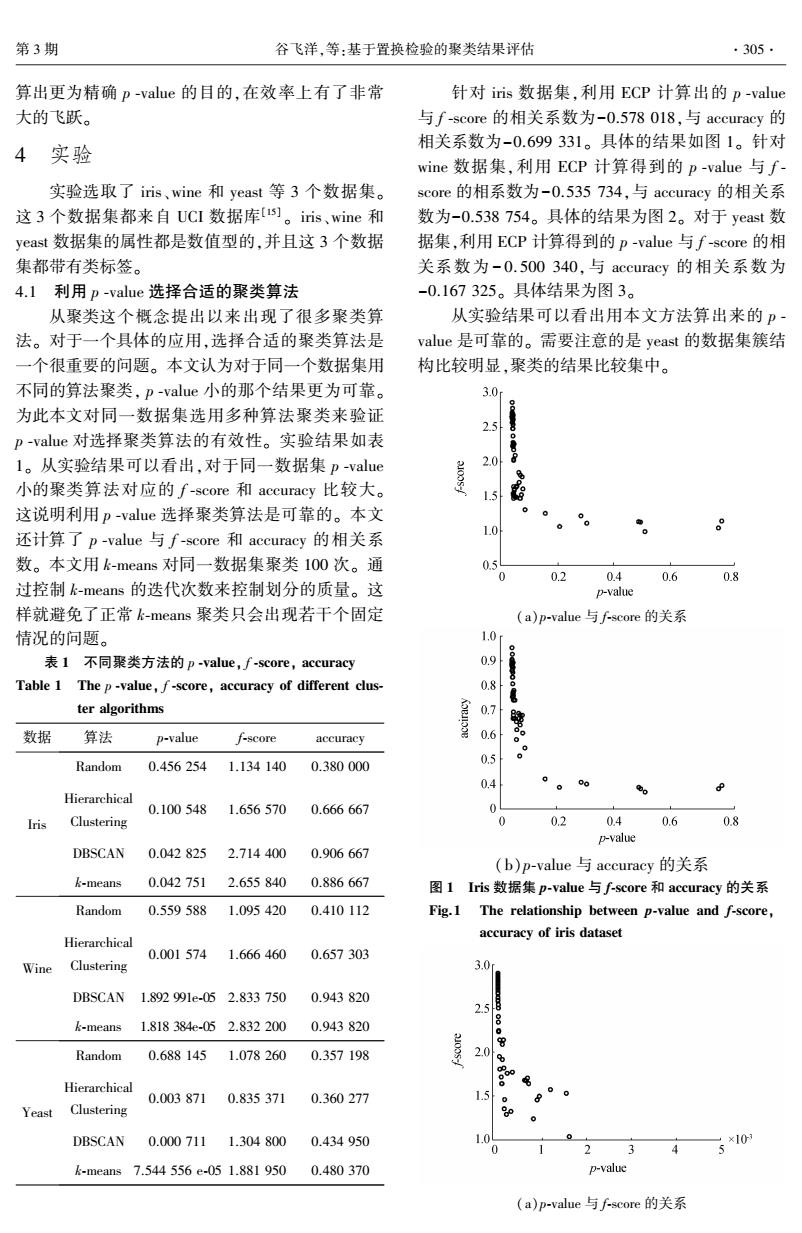
第3期 谷飞洋,等:基于置换检验的聚类结果评估 ·305. 算出更为精确p-value的目的,在效率上有了非常 针对iis数据集,利用ECP计算出的p-value 大的飞跃。 与f-score的相关系数为-0.578018,与accuracy的 4实验 相关系数为-0.699331。具体的结果如图1。针对 wine数据集,利用ECP计算得到的p-value与f 实验选取了iris、wine和yeast等3个数据集。 score的相系数为-0.535734,与accuracy的相关系 这3个数据集都来自UCI数据库。iis、wime和 数为-0.538754。具体的结果为图2。对于yeast数 yeast数据集的属性都是数值型的,并且这3个数据 据集,利用ECP计算得到的p-value与f-score的相 集都带有类标签。 关系数为-0.500340,与accuracy的相关系数为 4.1利用p-value选择合适的聚类算法 -0.167325。具体结果为图3。 从聚类这个概念提出以来出现了很多聚类算 从实验结果可以看出用本文方法算出来的P 法。对于一个具体的应用,选择合适的聚类算法是 value是可靠的。需要注意的是yeast的数据集簇结 一个很重要的问题。本文认为对于同一个数据集用 构比较明显,聚类的结果比较集中。 不同的算法聚类,p-value小的那个结果更为可靠。 3.0 为此本文对同一数据集选用多种算法聚类来验证 2.5 p-value对选择聚类算法的有效性。实验结果如表 。 1。从实验结果可以看出,对于同一数据集p-value 2.0 8 小的聚类算法对应的f-score和accuracy比较大。 这说明利用p-value选择聚类算法是可靠的。本文 0 还计算了p-value与f-score和accuracy的相关系 o 数。本文用k-means对同一数据集聚类100次。通 0. 0 0.2 0.4 0.6 0.8 过控制k-means的迭代次数来控制划分的质量。这 p-value 样就避免了正常k-means聚类只会出现若干个固定 (a)p-value与f-score的关系 情况的问题。 1.0r 表1不同聚类方法的p-value,f-score,accuracy 0.9 Table 1 The p-value,f-score,accuracy of different clus- 0.8 ter algorithms 数据 算法 p-value f-score accuracy 0.6 Random 0.456254 1.134140 0.380000 0.5 0.4 P Hierarchical 0.100548 1.656570 0.666667 0 Iris Clustering 0.2 04 0.6 08 p-value DBSCAN 0.042825 2.7144000.906667 (b)p-value与accuracy的关系 k-means 0.042751 2.655840 0.886667 图1Iris数据集p-value与f~score和accuracy的关系 Random 0.5595881.095420 0.410112 Fig.1 The relationship between p-value and f-score, Hierarchical accuracy of iris dataset 0.0015741.666460 0.657303 Wine Clustering DBSCAN1.892991e-052.8337500.943820 2.58 k-means1.818384e-052.832200 0.943820 Random 0.6881451.0782600.357198 2.0 0 Hierarchical 0.0038710.835371 0.360277 1.5 Yeast Clustering DBSCAn 0.0007111.304800 0.434950 1.0 ×10 0 5 k-means7.544556e-051.881950 0.480370 p-value (a)p-value与f-score的关系
算出更为精确 p ⁃value 的目的,在效率上有了非常 大的飞跃。 4 实验 实验选取了 iris、wine 和 yeast 等 3 个数据集。 这 3 个数据集都来自 UCI 数据库[15] 。 iris、wine 和 yeast 数据集的属性都是数值型的,并且这 3 个数据 集都带有类标签。 4.1 利用 p ⁃value 选择合适的聚类算法 从聚类这个概念提出以来出现了很多聚类算 法。 对于一个具体的应用,选择合适的聚类算法是 一个很重要的问题。 本文认为对于同一个数据集用 不同的算法聚类, p ⁃value 小的那个结果更为可靠。 为此本文对同一数据集选用多种算法聚类来验证 p ⁃value 对选择聚类算法的有效性。 实验结果如表 1。 从实验结果可以看出,对于同一数据集 p ⁃value 小的聚类算法对应的 f ⁃score 和 accuracy 比较大。 这说明利用 p ⁃value 选择聚类算法是可靠的。 本文 还计算了 p ⁃value 与 f ⁃score 和 accuracy 的相关系 数。 本文用 k⁃means 对同一数据集聚类 100 次。 通 过控制 k⁃means 的迭代次数来控制划分的质量。 这 样就避免了正常 k⁃means 聚类只会出现若干个固定 情况的问题。 表 1 不同聚类方法的 p ⁃value, f ⁃score, accuracy Table 1 The p ⁃value, f ⁃score, accuracy of different clus⁃ ter algorithms 数据 算法 p⁃value f⁃score accuracy Iris Random 0.456 254 1.134 140 0.380 000 Hierarchical Clustering 0.100 548 1.656 570 0.666 667 DBSCAN 0.042 825 2.714 400 0.906 667 k⁃means 0.042 751 2.655 840 0.886 667 Wine Random 0.559 588 1.095 420 0.410 112 Hierarchical Clustering 0.001 574 1.666 460 0.657 303 DBSCAN 1.892 991e⁃05 2.833 750 0.943 820 k⁃means 1.818 384e⁃05 2.832 200 0.943 820 Yeast Random 0.688 145 1.078 260 0.357 198 Hierarchical Clustering 0.003 871 0.835 371 0.360 277 DBSCAN 0.000 711 1.304 800 0.434 950 k⁃means 7.544 556 e⁃05 1.881 950 0.480 370 针对 iris 数据集,利用 ECP 计算出的 p ⁃value 与 f ⁃score 的相关系数为-0.578 018,与 accuracy 的 相关系数为-0.699 331。 具体的结果如图 1。 针对 wine 数据集,利用 ECP 计算得到的 p ⁃value 与 f ⁃ score 的相系数为-0.535 734,与 accuracy 的相关系 数为-0.538 754。 具体的结果为图 2。 对于 yeast 数 据集,利用 ECP 计算得到的 p ⁃value 与 f ⁃score 的相 关系数为 - 0. 500 340,与 accuracy 的相关系数为 -0.167 325。 具体结果为图 3。 从实验结果可以看出用本文方法算出来的 p ⁃ value 是可靠的。 需要注意的是 yeast 的数据集簇结 构比较明显,聚类的结果比较集中。 (a)p⁃value 与 f⁃score 的关系 (b)p⁃value 与 accuracy 的关系 图 1 Iris 数据集 p⁃value 与 f⁃score 和 accuracy 的关系 Fig.1 The relationship between p⁃value and f⁃score, accuracy of iris dataset (a)p⁃value 与 f⁃score 的关系 第 3 期 谷飞洋,等:基于置换检验的聚类结果评估 ·305·